1.2. Частотные характеристики линейных цепей

Рассмотрим воздействие на линейную стационарную цепь комплексного гармонического сигнала x(t) вида (10). Запишем реакцию цепи в виде интеграла Дюамеля

.

В силу условия казуальности нижний предел в этом интеграле можно заменить на –, в установившемся режиме при t > _у верхний предел также можно устремить к  и записать:

,

(11)

где

.

(12)

Комплексная функция частоты K(j) носит название частотной характеристики линейной стационарной цепи; ее модуль k() =K(j)называется амплитудно-частотной характеристикой (АЧХ), а аргумент () = arg(K(j)) – фазочастотной характеристикой (ФЧХ).

Используя формулу Эйлера и соотношение (11), вычислим реакцию линейной цепи на синусоидальный входной сигнал:

Таким образом, в установившемся режиме отклик линейной цепи на гармонический входной сигнал также является гармоническим сигналом, причем частоты входного и выходного сигналов равны. Амплитуда и фаза выходного сигнала при этом определяются выражениями:

.

(13)

Формула (13) описывает метод измерения АЧХ линейной стационарной цепи на заданной частоте как отношение амплитуды выходного сигнала к амплитуде входного гармонического сигнала; аналогично ФЧХ линейной цепи на заданной частоте определяется как сдвиг фаз между входным и выходным гармоническими сигналами. При использовании метода комплексных амплитуд частотная характеристика цепи определяется как отношение комплексных амплитуд гармонических сигналов на входе и выходе.

Поскольку произвольный периодический сигнал x(t), поданный на вход линейной стационарной цепи, может быть представлен рядом Фурье, то есть в виде линейной комбинации гармонических сигналов с кратными частотами, пользуясь формулами (5) и (13) легко записать выражение для выходного сигнала:

.

Из этой формулы следует, что реакция линейной стационарной цепи на периодический входной сигнал является периодическим сигналом с тем же периодом; при этом форма сигнала изменяется, поскольку амплитуды и фазы гармоник изменяются непропорционально.

Рассмотрим прохождение произвольного (непериодического) сигнала через линейную нестационарную цепь. Пользуясь представлением выходного сигнала в виде свертки импульсной характеристики со входным сигналом и теоремой о свертке, запишем выражение для спектральной плотности сигнала на выходе:

.

Возьмем линейную стационарную цепь с сосредоточенными параметрами, связь сигналов на входе и выходе которой описывается линейным дифференциальным уравнением с постоянными коэффициентами:

Следует отметить, что все цепи, состоящие из резисторов, конденсаторов и индуктивностей, а также значительная часть активных цепей описываются уравнениями такого вида. Применив преобразование Фурье к правой и левой частям этого равенства, получим уравнение, связывающее спектры входного и выходного сигналов

и частотную характеристику

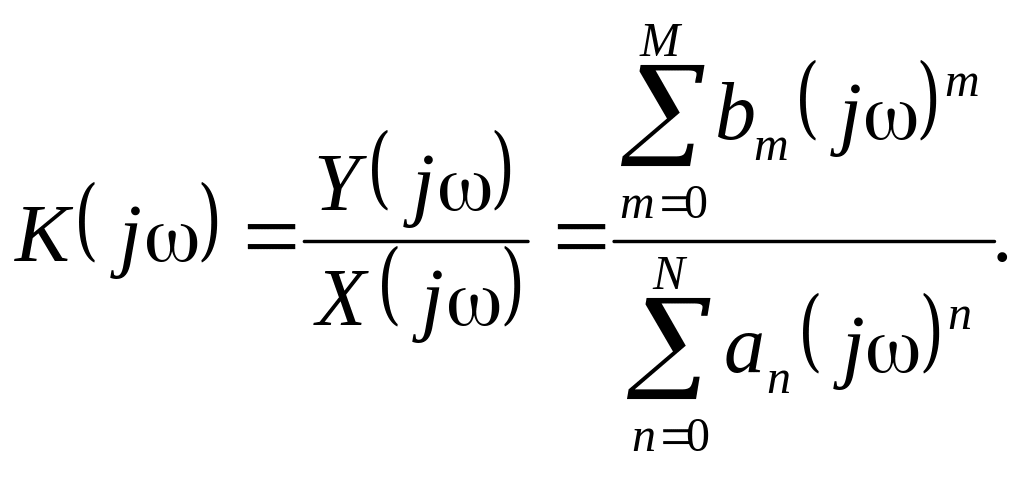
Таким образом, частотные характеристики стационарных линейных систем с сосредоточенными параметрами представляют собой отношения полиномов частоты. Степень полинома знаменателя N в полученном выражении называют порядком цепи. Если цепь физически реализуема, ее частотная характеристика должна стремиться к нулю при   ; это означает, что степень полинома числителя частотной характеристики должна быть меньше степени полинома знаменателя M < N.

Рис. 3. Пример неискаженной передачи сигнала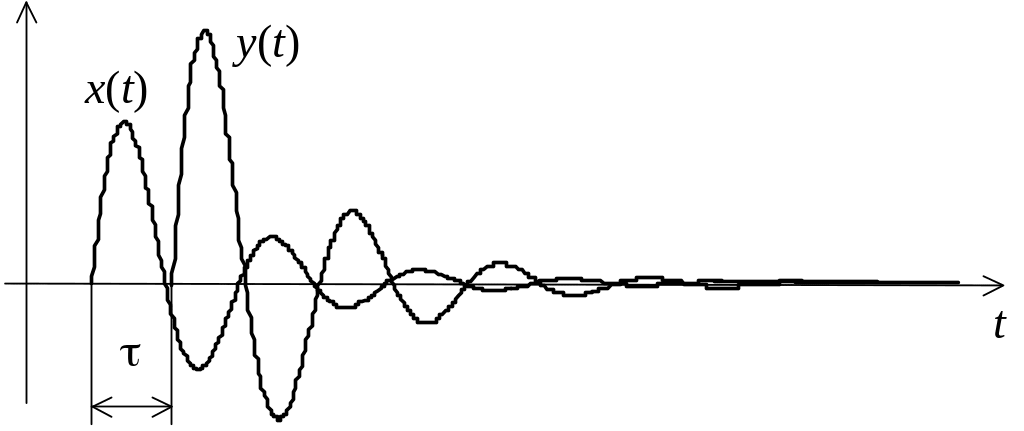

В заключение определим условие, при котором сигнал, пройдя через линейную цепь, не изменяет своей формы – условие неискаженной передачи сигнала. При этом может измениться его амплитуда и появиться сдвиг во времени (рис. 3), то есть

.

Взяв преобразование Фурье от этого выражения, получим

.

Таким образом, для того, чтобы цепь не искажала формы сигнала, ее АЧХ должна быть постоянной, а ФЧХ – линейной функцией частоты. Заметим, что выполнения этого условия достаточно только в том частотном диапазоне, где спектр входного сигнала X(j) отличен от нуля.