
- •А.В. Никитин, а.Л. Якимец основы радиоэлектроники
- •Часть 1. Линейные цепи
- •Введение
- •Лабораторная работа № 1 временные методы исследования линейных цепей
- •1. Теоретические сведения
- •1.1. Динамическое представление сигналов
- •1.2. Линейные стационарные цепи
- •1.3. Временные характеристики линейных цепей
- •2. Описание экспериментальной установки и методика измерений
- •3. Порядок выполнения работы
- •4. Контрольные вопросы
- •Лабораторная работа № 2 спектральные методы исследования линейных цепей
- •1. Теоретические сведения
- •1.1. Спектральное представление сигналов
- •1.2. Частотные характеристики линейных цепей
- •2. Описание экспериментальной установки и методика измерений
- •3. Порядок выполнения работы
- •4. Контрольные вопросы
- •Лабораторная работа № 3 интегрирующие и дифференцирующие цепи
- •1. Теоретические сведения
- •1.1. Частотные характеристики дифференцирующих и интегрирующих цепей
- •1.2. Анализ погрешностей дифференцирующих и интегрирующих цепей
- •2. Описание экспериментальной установки
- •3. Порядок выполнения работы
- •4. Контрольные вопросы
- •Лабораторная работа № 4 пассивные фильтры
- •1. Теоретические сведения
- •1.1. Фильтр нижних частот
- •1.2. Фильтр верхних частот
- •1.3. Полосовой фильтр
- •1.4. Режекторный фильтр
- •2. Описание экспериментальной установки
- •3. Порядок выполнения работы
- •Лабораторная работа № 5 согласующий трансформатор
- •1. Теоретические сведения
- •1.1. Эдс самоиндукции
- •1.2. Эдс взаимной индукции
- •1.3. Трансформатор
- •1.4. Режим согласования
- •2. Описание экспериментальной установки и методика измерений
- •3. Порядок выполнения работы
- •4. Контрольные вопросы
- •Лабораторная работа № 6 колебательные контуры
- •1. Теоретические сведения
- •1.1. Последовательный колебательный контур
- •1.2. Параллельный колебательный контур
- •2. Описание экспериментальной установки
- •3. Порядок выполнения работы
- •4. Контрольные вопросы
- •Список рекомендованной литературы
- •Содержание
- •Основы радиоэлектроники
- •Часть 1. Линейные цепи
- •400062, Г. Волгоград, ул. 2-я Продольная, 30.
Лабораторная работа № 1 временные методы исследования линейных цепей
Цель работы: Изучение методов измерения временных характеристик линейных цепей и способов их применения для расчета отклика цепи на заданное входное воздействие.
1. Теоретические сведения
Временные методы анализа линейных стационарных цепей основаны на принципах динамического представления сигналов, а также – на свойствах линейных операторов, описывающих цепь.
1.1. Динамическое представление сигналов
Смысл динамического представления состоит в приближении исследуемого сигнала взвешенной суммой некоторых элементарных сигналов, возникающих в последовательные моменты времени. В пределе, при стремлении временных интервалов между соседними элементарными сигналами к нулю, получается точное представление исходного сигнала. При этом в качестве элементарных сигналов обычно используют обобщенные функции – функцию Хевисайда или -функцию Дирака.
Рассмотрим сигнал, математической моделью которого является функция Хевисайда (функция включения), описываемая выражением
|
(1) |
Форма (1) не является единственно возможным способом определения функции включения. Так, например, она может быть описана с помощью предела
![]() .
.
Рассмотрим произвольный сигнал x(t), такой, что x(t) = 0 при t < 0, и представим его в виде суммы функций включения, возникающих в моменты времени tk = kt (рис. 1, а)
![]() .
.
Домножив и поделив сумму в этом выражении на шаг дискретизации t и устремляя его к нулю, получим
|
(2) |
Это формула динамического представления сигнала посредством функции Хевисайда. Интеграл (2) называют интегралом наложения (интегралом Дюамеля).
Рассмотрим другой способ представления сигналов. Введем -функцию Дирака как предел последовательности прямоугольных импульсов длительностью при 0
|
(3) |
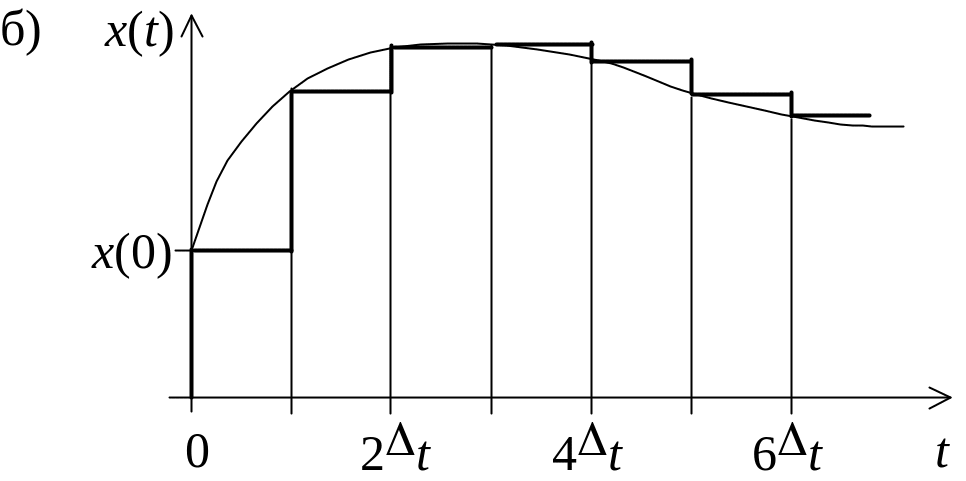
Рис. 1. Представление
сигнала x(t)
в виде суперпозиции функций включения
(а)
и суперпозиции
прямоугольных импульсов (б)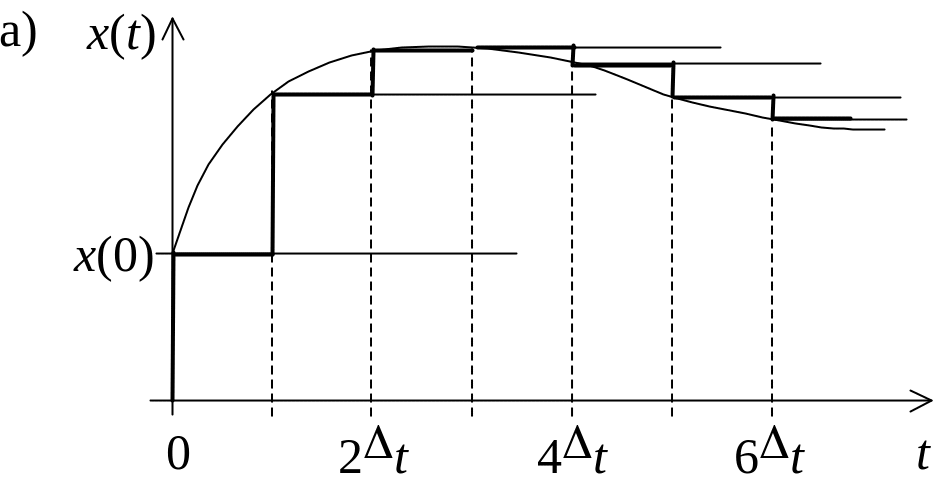 EMBED Word.Picture.8
EMBED Word.Picture.8
Одним из самых интересных свойств -функции является ее фильтрующая способность. Можно сформулировать это свойство следующим образом: интеграл от произведения произвольной функции f(t) такой, что
![]() ,
,
на -функцию дает значение f(0), то есть
|
(4) |
Именно соотношение (4) в математике используют как определение обобщенной функции (t). Доказано, что свойствами -функции обладают пределы последовательностей следующих функций
![]() .
.
Пользуясь соотношением (4), легко показать, что фильтрующие свойства -функции сохраняются и при ее временном сдвиге, то есть
![]() .
.
Представим сигнал x(t) в виде суммы прямоугольных импульсов равной длительности, возникающих в моменты времени tk = kt и имеющих высоту x[k] = x(kt), как это показано на рис.1, б:
![]() .
.
Домножив и разделив это выражение на t и устремив t к нулю, получим
|
(5) |
Интеграл вида (5)
называют сверткой
функций x(t)
и (t)
и обозначают следующим образом:![]() .
.

