§ 24. Оператор Гамильтона различных систем

Этот вопрос идентичен вопросу рассмотренному в классической механике - будут те же соотношения, но для операторов

.

Поставим в соответствие конкретной системе операторы и :

В декартовой системе координат , .

Здесь n – число точек в системе.

.

- функция от оператора координаты.

Мы рассматриваем - представление, здесь

Мы рассматриваем декартову систему координат. Гамильтониан мы поставили в соответствие системе материальных точек. Эта система незамкнутая, т. к. потенциальная энергия зависит от времени. (т. е. здесь нет однородности времени).

Перейдем к более простой задаче. Рассмотрим систему N материальных точек во внешнем стационарном поле

Здесь отвечает за внутреннее взаимодействие между частицами.

отвечает за внешнее воздействие на систему частиц.

.

Выражение, описывающее внешнее воздействие обладает аддитивностью, т. е.

.

Индекс a означает, что разные частицы могут взаимодействовать с внешним полем по разному закону. Если все частицы одинаковые и одинаково взаимодействуют с внешним полем, то индекс a убирается.

Внутреннее взаимодействие неаддитивно.

Рассмотрим случай свободной материальной точки. Соответственно она ни с чем не взаимодействует:

Тогда , или в -представлении, то

,

тогда .

Если материальная точка во внешнем поле:

, ,

Нестационарное поле .

Стационарное поле .

Центральное поле .

Рассмотрим систему двух материальных точек. Мы рассматриваем частный случай – замкнутая система двух материальных точек.

В случае классической механики: .

Отсутствие t в энергии взаимодействия – это однородность времени и закон сохранения энергии.

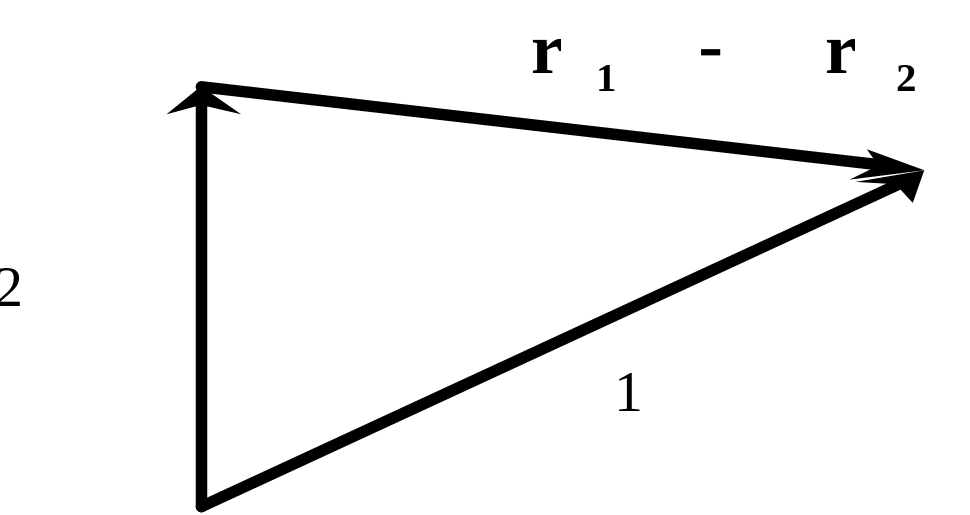
Зависимость энергии от модуля есть изотропность пространства.

В квантовой механике в -представлении:

,

,

где

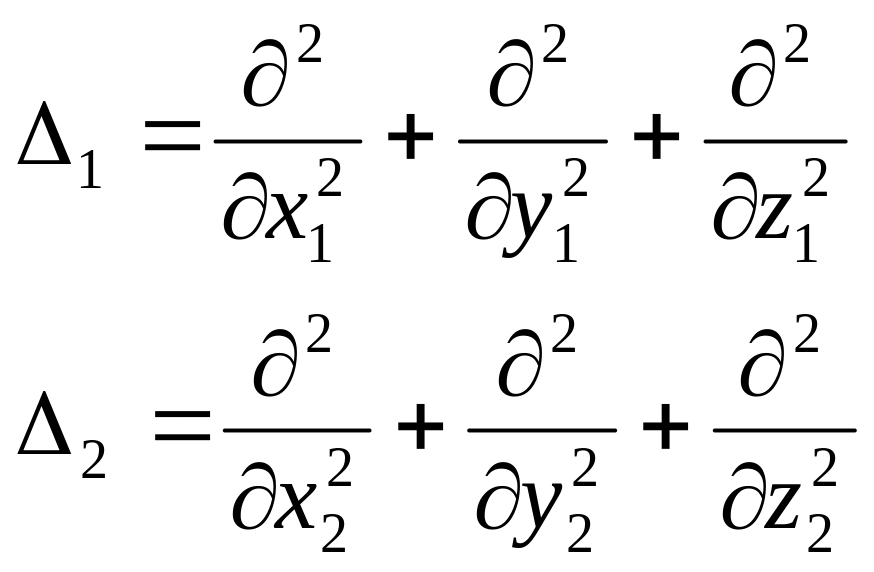
§ 25. Стационарное состояние различных систем

Задача на собственные функции и собственные значения для оператора :

(25.1)

Волновое уравнение:

(25.2)

Как только поставили в соответствие системе оператор , то можем решать волновое уравнение, находим , которая определяет состояние системы.

Собственные функции задачи (25.1) и функции, являющиеся решением волнового уравнения совпадают при условии выполнения:

, тогда . Это условие совместности решений (25.1) и (25.2).

Так как , то гамильтониан системы явно от времени не зависит, т. е. поле стационарно (задача стационарна) – это говорит о совместности решений (25.1) и (25.2).

Рассмотрим стационарную задачу , тогда не зависит от времени. Это либо:

Замкнутая система.

Система в стационарном внешнем поле.

Используя (25.1) и (25.2), получим

Это дифференциальное уравнение имеет решение

Подставим эту функцию в (25.1), тогда

.

Тогда получим

Получили стационарное уравнение Шредингера.

§ 26. Решение волнового уравнения в случае свободной материальной точки

Для свободной материальной точки .

, тогда переходим к стационарному уравнению Шредингера.

Это трехмерная задача

Оператор Лапласа

Оператор представим в виде суммы трех независимых операторов, которые коммутируют. В этом случае можно разделить переменные.

Тогда стационарное уравнение Шредингера запишется в виде

,

где

Для имеем

.

Обозначим

.

Тогда

Решение этого уравнения

Так как частица свободная, то импульс этой частицы сохраняется. Значит, сохраняется направление движения частицы.

Мы выбираем движение частицы по направлению оси x. Тогда в силу сохранения импульса имеем .

Для трехмерного случая

Полная волновая функция

(26.1)

Рассмотрим теперь коммутатор

Так как импульс коммутирует с и не зависит явно от времени, тогда . Из этого следует:

-интеграл движения.

Собственная функция оператора импульса является решением волнового уравнения.

Найдем собственные значения оператора импульса.

{используем, что , т. е. } =

= .

Тогда собственное значение оператора :

Это первое дебройлевское соотношение.

Из (26.1) вводится - второе дебройлевское соотношение.

Используем, что

Уравнение (26.1) удовлетворяет собственной функции оператора импульса.