§6. Роль классической механики в квантовой механике

Два момента присутствия классической механики в квантовой механике:

1. Измерение микросистем (квантово-механических систем) проводятся с помощью классических приборов (систем).

2. Принцип соответствия – переход квантово-механических результатов в классическую механику (  0, можно ввести такую величину размерности действия A, что ). По Эйнштейну этот переход характеризуется . Если , то переход в классическую механику Ньютона.

§7. Волновая функция и ее свойства

Волновая функция динамических переменных и времени определяет состояние системы с точностью до фазового множителя, т. е.

т. е. и описывает одно и тоже состояние, где - фазовый множитель. Волновая функция – комплексная, непрерывная, конечная. У нее почти всюду существует конечная производная по координате, но в некоторых точках может терпеть скачек (особые точки). Функции - нормируемые, т.е. квадратично интегрируемы. Но для свободной материальной точки не нормируема.

- элементарный объем

- вероятность того, что динамические переменные лежат в интервале . Это определение справедливо для квадратично интегрируемых функций. Для не квадратично интегрируемых функций величина пропорциональна плотности вероятности.

§8. Принцип суперпозиции состояний

Если мы имеем состояния системы, описываемые функциями , то суперпозиции этих функций также отвечает некоторое состояние этой системы:

Отсюда получаем: уравнения, которым подчиняется функция должны быть линейными. Этот же вывод распространяется и на операторы в квантовой механике. Принцип суперпозиции требует использования в квантовой механике линейных операторов.

§9. Понятие о теории представлений

Представление – это совокупность переменных, в которых решается задача (т. е. набор динамических переменных). Рассмотрим одну материальную точку. Число степеней свободы n=3. Здесь могут быть 2 случая:

1. Под понимаем 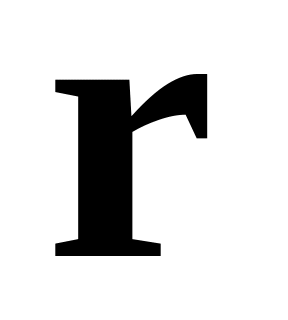_- имеем -представление (координатное)

Оператор координаты

Оператор импульса

Здесь

2. Под понимаем - имеем -представление (импульсное)

Оператор координаты

Оператор импульса

Здесь

Мы в основном будем использовать -представление. Результаты измерения от вида представления не зависят!

§10. Операторы в квантовой механике

В силу принципа суперпозиции в квантовой механике используются линейные операторы. Задача на собственные функции и собственные значения:

Определение оператора:

Свойство линейности:

Если , то

т.к. , то

Сопряженный оператор – это оператор, который связан с данным оператором соотношением:

или

Тогда получаем:

Если - то оператор называется эрмитовым (самосопряженным).

Транспонированный оператор

Отметим следующие свойства:

1)

(10.1)

Из выражения (10.1) получаем:

2)

3)

Сумма операторов: . Это операторное равенство предполагает

Произведение операторов: , тогда . Это операторное равенство предполагает

В общем случае не коммутативны

Коммутатор

Если , то операторы и называются коммутативными (операторы и коммутируют).

Если , то операторы и называются не коммутативными (операторы и не коммутируют).

Так как физические величины вещественны, то число операторов в квантовой механике ограничено. Собственные значения эрмитовых операторов вещественны, значит только их можно ставить в соответствие физическим величинам.

Запишем определение среднего:

Так как результаты измерений вещественны, то тоже должно быть вещественным, т.е.

(10.2)

тогда

,

т.е.

Обозначим , тогда

Тогда из (10.2) получаем

(10.3)

Из (10.3) имеем для любых :

,

,

где (сопряженный и транспонированный).