- •§1. Экспериментальные основы квантовой механики
- •§2. Классическое и квантовое описание системы
- •§3. Принцип неопределенности
- •§4. Полный набор динамических переменных
- •§5. Постулаты квантовой механики
- •§6. Роль классической механики в квантовой механике
- •§7. Волновая функция и ее свойства
- •§8. Принцип суперпозиции состояний
- •§9. Понятие о теории представлений
- •§10. Операторы в квантовой механике
- •Транспонированный оператор
- •§11. Собственные функции и собственные значения эрмитовых операторов. Случай дискретного и непрерывного спектра
- •§12. Среднее значение измеряемой величины
- •§13. Вероятность результатов измерения
- •§14. Коммутативность операторов и одновременная измеримость физических величин
- •§15. Операторы координаты , импульса , момента импульса , энергии
- •§16. Решение задачи на собственные функции и собственные значения для оператора
- •§17. Решение задачи на собственные функции и собственные значения для оператора
- •§ 18. Вычисление коммутаторов, содержащих операторы
- •§ 19. Волновое уравнение
- •§ 20. Производная оператора по времени
- •§ 21. Интегралы движения в квантовой механике
- •§22. Флуктуации физических величин
- •§ 23. Неравенство Гейзенберга
- •§ 24. Оператор Гамильтона различных систем
- •§ 25. Стационарное состояние различных систем
- •§ 26. Решение волнового уравнения в случае свободной материальной точки
- •§ 27. Решение волнового уравнения в случае бесконечно глубокой потенциальной ямы
- •§ 28. Потенциальный барьер конечной высоты
- •§ 29. Вид операторов и в декартовых и сферических координатах
- •§ 30. Коммутационные соотношения с оператором
- •§ 31. Собственные функции и собственные значения операторов и
- •§ 32. Собственный механический момент (спин)
- •§ 33. Операторы и и их свойства
- •§ 34. Спиновая переменная волновой функции
- •§ 35. Матрицы Паули и их свойства
- •§ 36. Уравнение Паули Мы писали волновое уравнение в виде
- •§ 37. Принцип тождественности
- •§ 38. Оператор перестановки и его свойства
- •§39. Симметричное и антисимметричное состояния
- •§40. Обменное взаимодействие
- •§41. Основное состояние атома гелия
- •§42. Стационарная теория возмущений в случае невырожденного дискретного энергетического спектра: нулевое и первое приближения
- •§43. Стационарная теория возмущений в случае невырожденного дискретного энергетического спектра: второе приближение
- •§44. Критерий применимости теории возмущений
- •§45. Стационарная теория возмущений в случае близких энергетических уровней.
- •Задачи по курсу «Квантовая статистика» (Часть I) и их решение
- •Вопросы для экзамена по квантовой механике (программа минимум).
§ 27. Решение волнового уравнения в случае бесконечно глубокой потенциальной ямы
В случае бесконечно глубокой ямы по определению имеем
![]()
Интересующее нас решение ищем на отрезке
![]() .
.
Поскольку в точках x=0 и x=a потенциальная энергия частица обращается в бесконечность, вероятность преодоления бесконечного барьера и попадания за пределы области равна нулю. Оказавшись в этой области частица все время будет находиться в ней. Из определения волновой функции следует
![]()
где в.ф. удовлетворяет стационарному уравнению Шредингера
совпадающему с определением оператора
,
т.е. функция
есть собственная функция этого оператора,
соответствующая собственному значению
Е. Из сказанного вытекают граничные
условия
![]() ,
накладываемые на решение уравнения.
,
накладываемые на решение уравнения.
Таким образом, приходим к задаче
![]()
От сюда следует:
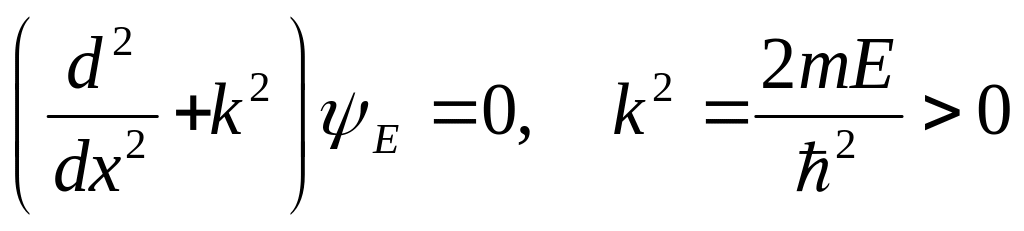 (*)
(*)
Положительность собственного значения
Е оператора
вытекает из положительности
![]() .
Решение уравнения (*) представимо в виде
суперпозиции двух элементарных состояний,
которые на языке
.
Решение уравнения (*) представимо в виде
суперпозиции двух элементарных состояний,
которые на языке
![]() интерпретируются
как волны де Бройля, распространяющиеся
в противоположных направлениях оси x:
интерпретируются
как волны де Бройля, распространяющиеся
в противоположных направлениях оси x:
![]()
Подстановка решения в граничные условия приводит к системе однородных уравнений
![]() (**)
(**)
Для неизвестных коэффициентов С+/_. Критерий существования нетривиального решения данной системы
![]()
дает условие квантования
![]()
собственного значения Е. Это означает, что обладает дискретным спектром. Вводя согласно (**) обозначения
![]()
где С- неизвестная пока вещественная (в силу наличия у в.ф. произвольного фазового множителя) константа, для искомой в.ф. будем иметь
![]()
Поскольку собственные функции оператора с дискретным спектром квадратично интегрируемы, условие нормировки имеет вид
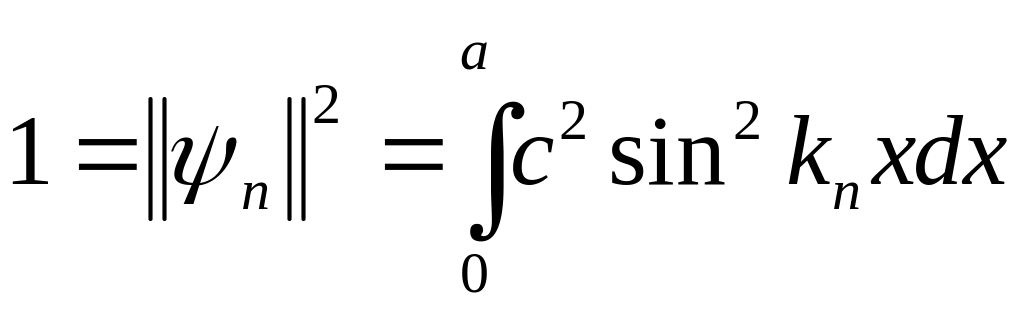
От сюда, интегрируя, получаем
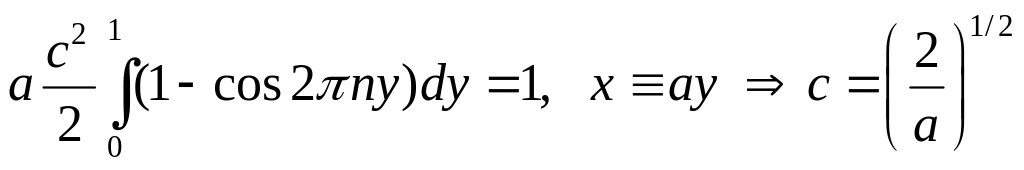
Подставляя найденное значение константы,
запишем решение задачи в окончательной
форме
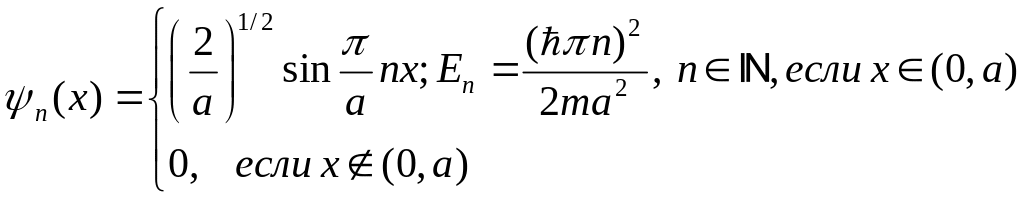 (13.2)
(13.2)
§ 28. Потенциальный барьер конечной высоты
Под потенциальным барьером понимают область пространства, где потенциальная энергия частицы увеличивается, а потом уменьшается. Как известно, в квантовой физике частица с некоторой вероятность может пройти сквозь потенциальный барьер.
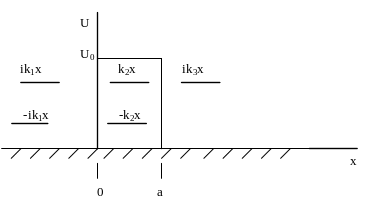
Запишем уравнение Шредингера:
Для первой и третьей области уравнение
запишется как
![]()
Для второй области
![]()
Решая уравнение Шредингера для каждой области, запишем волновые функции.
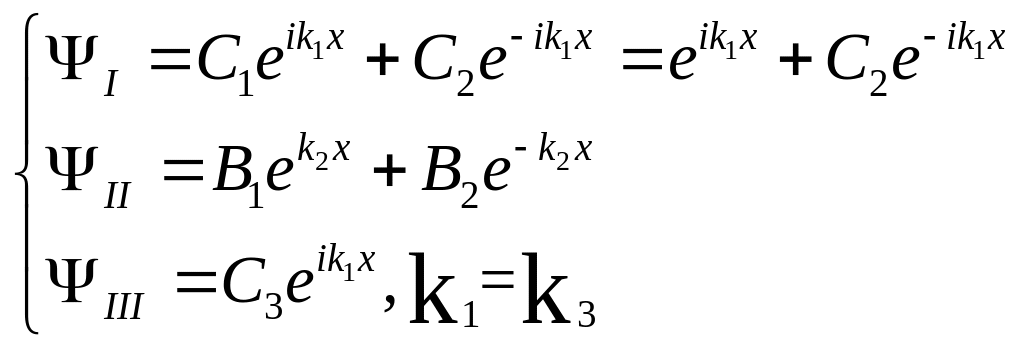
Где
![]()
Введем нормировку на единичный поток, то есть положим C1 =1.
«Сошьем» решения на границе областей, используя граничные условия (непрерывность в.ф. и ее производной на границе областей (конечный скачок U)):
![]()
Расписывая, получаем

Получили систему относительно переменных C2, C3, B1, B2. Решим её по правилу Крамера.
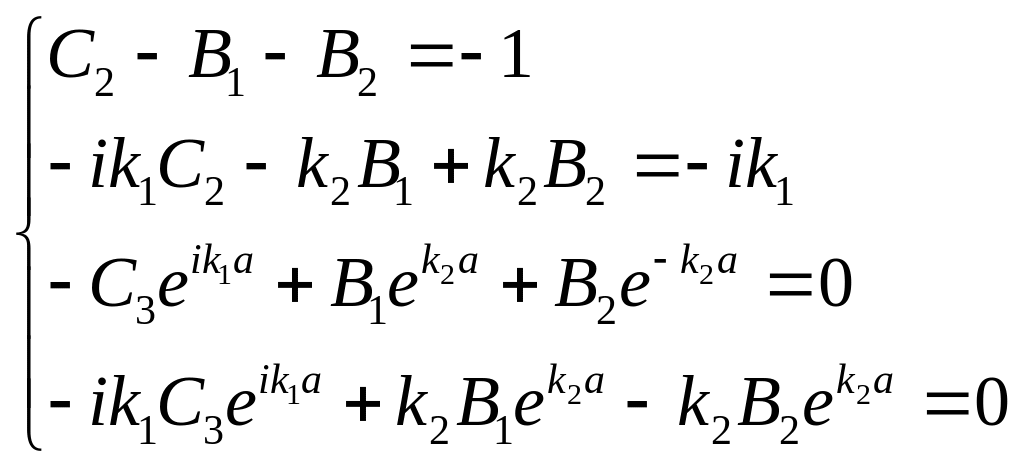
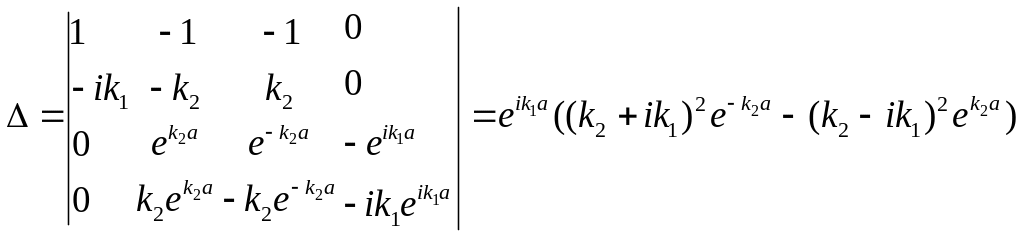
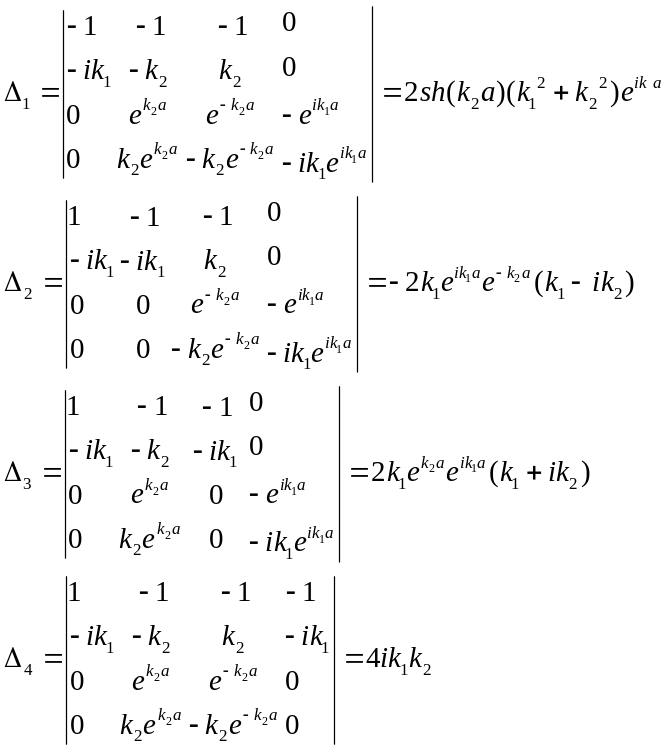
Теперь мы можем найти все неизвестные
коэффициенты по формуле
![]() :
:
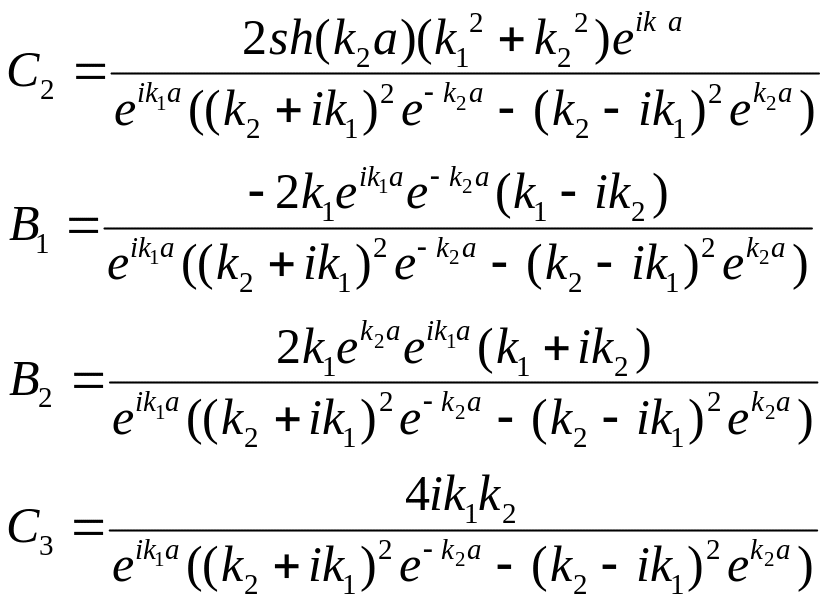
Отсюда мы можем найти коэффициенты
прохождения и отражения. По определению
![]() .
В нашем случае, коэффициенты будут
равны
.
В нашем случае, коэффициенты будут
равны