§3. Принцип неопределенности

Две формулировки:

1. В микромире понятие “траектория” отсутствует

2. Канонически сопряженные величины одновременно неизмеримы

В трехмерном пространстве канонически сопряженные величины будут:

p_x и x

p_y и y

p_z и z

Здесь n=3. Имеем 3 одновременно измеряемые динамические переменные. Например:

1. p_x. p_y. p_z

2. x, y, z

3. x, y, p_z и тд.

§4. Полный набор динамических переменных

Полный набор динамических переменных – это наибольший набор независимых одновременно измеряемых динамических переменных. Измерение полного набора динамических переменных полностью определяет состояние квантово-механической системы. Число динамических переменных в квантовой системе - n и по сравнению с классической системой (2n) уменьшается в 2 раза. Максимальный набор – это значит, что к этому набору не может быть добавлена ни одна другая переменная, которая не являлась бы их функцией. В этом случае они не зависимы. Каждая из этих переменных не является функцией другой переменной из этого же набора. Заметим, что здесь зависимость не линейная (как в линейной алгебре), а функциональная.

§5. Постулаты квантовой механики

Часто выделяют 4 постулата:

1. Постулат о волновой функции.

Каждой системе (состоянию кв.-мех. системы) может быть поставлена в соответствие волновая функция динамических переменных (из полного набора) и времени, полностью описывающей состояние системы.

Динамические переменные одновременно измеримы. - n – мерный вектор динамических переменных; функция динамических переменных и времени - описывает эволюцию квантово-механических систем. классической механике задание 2n динамических переменных полностью определяет состояние системы через функцию Гамильтона. В квантово-механической системе описывается эволюция системы через - функцию от n динамических переменных.

2. О связи физических величин и объектов математики (операторов).

Каждой физической величине (наблюдаемой) ставится в соответствие оператор: .

3. Связь между результатами измерения физической величины 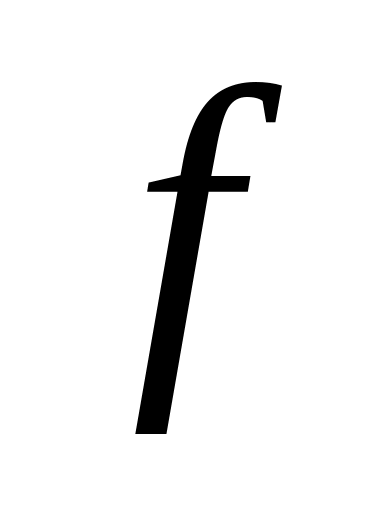и значением оператора (т. е. решением математических задач)

Пусть - значение физической величины , которое получено в результате измерения системы, находящейся в i-том квантовом состоянии.

является одним из собственных значений оператора . Это задача на собственные функции и собственные значения. Задача определяет собственные значения , соответствующие и определяет собственные функции , соответствующие собственным значениям . Если собственные значения образуют дискретное множество, то говорят о дискретном спектре. Если собственные значения образуют непрерывное множество, то спектр непрерывный.

4. Определение среднего значения физической величины

Здесь введено понятие скалярного произведения для функций из гильбертова пространства. Гильбертово пространство – это пространство квадратично интегрируемых функций (нормируемых функций). Если - квадратично интегрируемые функции, тогда:

Это определение для - декартовых переменных. Для перехода к другой системе координат вводится якобиан перехода. Значок «*» означает комплексное сопряжение.

Это аналог длины в векторном пространстве.