§40. Обменное взаимодействие
Рассмотрим пару частиц взаимодействующих друг с другом по кулоновскому закону и находящихся во внешнем поле.
Пусть рассматриваются электроны:
Внешним полем электрона может служить поле ядра.
Одночастичный оператор
, i=1,
2.
Используем принцип Паули несколько в
иной форме, чем мы рассматривали раньше.
Для этого пусть добавка
мала. Здесь спиновое число
.
Суммарный собственный механический
момент:
имеет квантовые числа
.
Учтем влияние спинового момента на волновые функции. Это достигается принципом тождественности. Т. к. электроны – фермионы, то суммарная волновая функция должна быть антисимметричной по перестановке и т. к. в гамильтониане нет спиновой зависимости, то можно разделить переменные, итак:
Эта функция антисимметричная, так как описывает фермионы. Здесь два варианта:
- антисимметричная
- симметричная.
или
- симметричная
- антисимметричная.
Антисимметричная спиновая функция приводит к суммарному спину 0.
Симметричная
волновая функция приводит к суммарному
спину 1.
Итак имеем 2 типа решения:
Спин
,
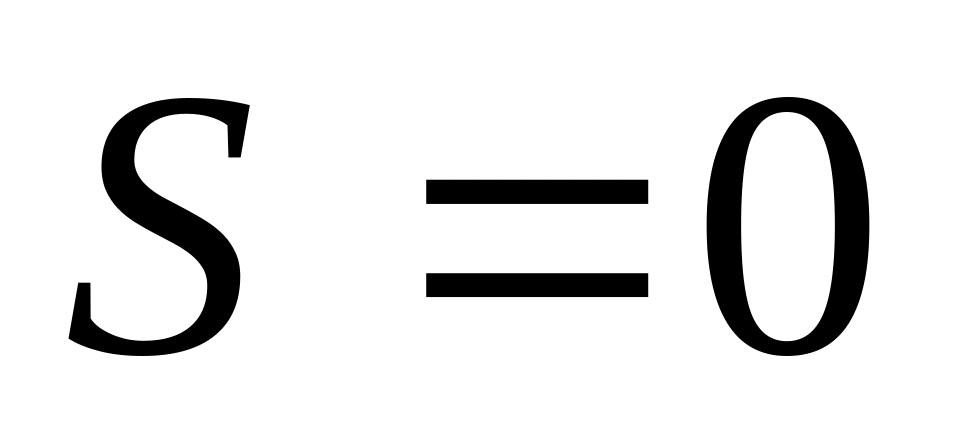симметричная координатная функция по
координатам
Спин S=1 , имеем антисимметричную функцию по координатам:
Но полная функция
-
антисимметричная.
Случай 1: S=0 – парагелий.
S=1 – ортогелий.
Функции
и
- явно от спина не зависят, но с учетом
принципа тождественности мы получили
два типа решения.
,
- это различные одночастичные состояния,
они удовлетворяют одночастичному
оператору:
Центральное поле.
У нас одночастичные
,
- это все одночастичные состояния.
Имеем задачу на собственные функции и собственные значения.
Функции
и
- описывают невзаимодействующие частицы,
т. е. они являются решением задачи с
оператором:
,
где
,
- одночастичные операторы.
Рассмотрим обменное взаимодействие . Т. к. и является решением задачи для невзаимодействующих частиц, т. е.
Здесь решение не зависит от симметричности
функций, т. е. здесь
.
Для полного оператора
- решение зависит от симметрии функции,
т. е. от спина системы: (0 или 1), здесь
.
В первом приближении теории возмущений найдем энергетические уровни:
,
где матричный элемент оператора возмущения
,
здесь
=>
.
В нашем случае индекс i складывается из индексов одночастичных состояний 1 и 2.
У нас
,
где K и A – это определенные выражения. Можно рассмотреть матричный элемент для симметричного состояния:
и можно рассмотреть матричный элемент для антисимметричного состояния
.
Это диагональные элементы, т. е. они берутся по одинаковым функциям, т. е. по и .
Подставим функции
и
в матричные элементы
и
и замечаем, что получим одинаковые
слагаемые и различные слагаемые, которые
соответственно обозначим:
,
где
(46.1)
, (46.2)
если учесть перестановку состояний ( а не координат), то имеем
(46.3)
В выражении (46.1), (46.2), (46.3) стоят координаты
,
,
а индексы при
обозначают состояния.
Тогда
.
Введем плотность заряда в точке 1 и в состоянии 1:
.
Аналогично для 2 точки и во втором состоянии:
,
тогда
.
Мы не можем привести интеграл
к такому же виду. Интеграл
- обменный интеграл. В нем
и
- одно состояние размазано по двум
точкам.
и
- в одной точке имеется два состояния.
Итак
,
.