§ 33. Операторы и и их свойства

Все проводится по аналогии с и .

обладает коммутационными свойствами:

Так как и не коммутируют, то они одновременно не измеримы.

Но .

Собственные значения оператора:

, .

Тогда здесь всего 2s+1 значение оператора.

Перейдем к классическому пределу:

Ввиду связи имеем , .

Ясно, что так как - параметр частицы, то он не меняется ни при каких условиях, тогда в классическом пределе:

, .

В классической механике этим величинам аналога нет и они обращаются в нуль.

В случае спина мы не можем наложить условие , т. к. спин – внутреннее свойство частицы. Тогда не всегда целое число.

Если - четное, то -полуцелое.

Если - нечетное, то -целое.

Отсюда деление на 2 типа частиц:

1. Фермионы – спин полуцелый

2. Бозоны – спин целый.

§ 34. Спиновая переменная волновой функции

Рассмотрим одну частицу – система с 3 степенями свободы. Задача решается в - представлении.

,

но есть еще внутренний параметр – спин, тогда

.

Здесь - переменная (пространственная координата) и (спиновая переменная, а именно проекция спина на ось ).

Здесь мы рассматриваем стационарную задачу, поэтому от t не зависит.

Скалярное произведение теперь запишем в виде

Вероятность обнаружения частицы в объеме вблизи точки :

Если хотим найти реализацию конкретного значения :

Рассмотрим действие операторов в пространстве четырех переменных

Было известно

(40.1)

Обобщим (40.1) на случай четырех переменных:

(40.2)

Рассмотрим случай когда действует только на спиновую переменную. В этом случае ядро будет следующим

и интеграл (40.2) переходит в интеграл:

Тогда

Переменная здесь не играет большой роли. В дальнейшем будем ее опускать, тогда

Функция имеет 2s+1 переменную.

Ядро в дискретных переменных вырождается в матрицу, т. е. это есть матрица размером .

§ 35. Матрицы Паули и их свойства

Рассмотрим электрон со спином . Тогда матрицы, которые будут представлять спиновые моменты имеют размерность

.

Рассмотрим представление (или - представление). Рассмотрим в этом представлении матрицу Это оператор в матричном представлении.

Мы помним, что в матричном представлении ядро оператора имело вид

.

Тогда для нашего представления имеем:

Аналогично матрицы

,

,

.

и не диагональные матрицы, тогда эти величины с одновременно не измеримы. По главной диагонали стоят собственные значения.

Вводятся матрицы . Это матрицы Паули.

Тогда

,

,

.

Легко показать, что

.

Или на языке операторов

А коммутаторы:

,

.

Тогда так как , то получим

При :

Тогда

При получаем

.

§ 36. Уравнение Паули Мы писали волновое уравнение в виде

,

здесь

Для одной материальной точки :

1. Без магнитного поля .

2. Если есть магнитное поле, то .

В этих случаях спин не учтен.

С учетом спина модификацию уравнений сделал Паули.

Примечание: уравнения Шредингера и Паули нерелятивистские.

Запишем уравнение Паули:

.

Здесь изменился оператор кинетической энергии.

Без учета магнитного поля

,

где

Здесь

- матрицы Паули

Тогда

.

Покажем, что при отсутствии поля, имеем

,

т. е.

Рассмотрим

={так как действует на спиновую переменную, а на пространственную, то и коммутативны.} = =

={рассмотрим сумму когда и когда }= ={рассмотрим .

, т. к.

}=[

При :

Рассмотрим случай когда есть магнитное поле:

.

Тогда для оператора имеем

Тогда оператор кинетической энергии из оператора Паули:

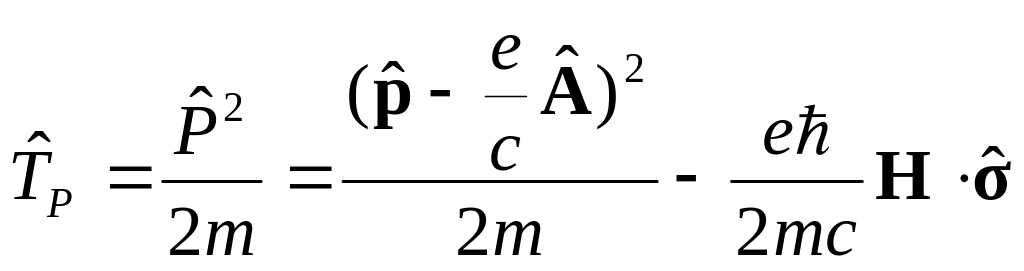
Рассмотрим случай электрона e<0.

(магнетон Бора)

Тогда в итоге получаем:

,

где оператор

Для оператора Паули тогда получим

,

Отсюда видно равенство для гиромагнитных отношений

Видно, что магнитные моменты

,

,

механические моменты

Гиромагнитные отношения

.

Полный магнитный момент