Лекции по гетеропереходам / курс лекций физика и технология полупроводниковых наноструктур / 07_ур-нение Шредингера

Уровни энергии в потенциальной квантовой яме

Узкозонный полупроводник, помещенный в матрицу широкозонного материала, может рассматриваться как потенциальная яма для носителей заряда. Наличие потенциальных барьеров влияет на энергетический спектр носителей заряда и может быть рассмотрено в рамках упрощенных представлений квантовой механики.

Стационарными состояниями системы в квантовой механике называются такие состояния, в которых энергия имеет определенные значения, остающиеся постоянными во времени.

А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 7, стр. 1

Волновое уравнение для стационарных состояний имеет вид

ˆψ = ψ

H E

Здесь ˆ - оператор Гамильтона

H

ψ - волновая функция стационарного состояния Е – собственные значения энергии

Гамильтониан для одной частицы, находящейся во внешнем поле U(x,y,z) имеет вид

где ∆ = ∂2 ∂x2 +∂2 ∂y2 +∂2 ∂z2 оператор Лапласа

А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 7, стр. 2

Соответственно, волновое уравнение, определяющее стационарное состояние, принимает вид

h2 ∆ψ +[E −U (x, y, z)]ψ = 0 2m

Это уравнение было установлено в 1926 г. Шредингером.

Для свободной частицы уравнение Шредингера принимает вид

h2 ∆ψ + Eψ = 0 2m

А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 7, стр. 3

Вэтом случае уравнение имеет решения при любом положительном значении энергии Е, причем E = p2 2m

Вслучае плоской квантовой ямы потенциальная энергия зависит только от одной координаты х. В этом случае волновая функция является произведением функции от y и z на функцию только от х. Первая функция определяется уравнением Шредингера для свободного движения, а вторая

– одномерным уравнением Шредингера

d 2ψ + 2m [E −U (x)]ψ = 0 dx2 h2

А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 7, стр. 4

Решением для собственных значений энергии являются дискретные уровни. Причем, для них справедлива осцилляционная теорема: Волновая функция дискретного спектра, соответствующая n+1 собственному значению энергии обращается в нуль n раз при конечных значениях х.

В интересующем нас случае зависимость потенциальной энергии от координаты может быть представлена в виде прямоугольной потенциальной ямы.

А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 7, стр. 5

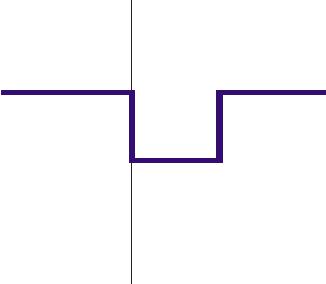
U(x)

U0

U (x) = 0 при 0 < x < L и U (x) =U 0 при x > L или x < 0

L имеет смысл физической ширины квантовой ямы

U0 имеет смысл величины разрыва зоны проводимости (или валентной зоны) на гетерогранице для случая электронного (дырочного) кванования.

А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 7, стр. 6

В случае полупроводников в качестве m должна быть взята эффективная масса для соответствующего типа носителей, которая описывает влияние кристаллической решетки на движение носителя заряда.

Эффективные массы носителей заряда для некоторых прямозонных полупроводниковых материалов A3B5

А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 7, стр. 7

В области квантовой ямы (0<x<L) уравнение Шредингера имеет вид

d 2ψ + 2m Eψ = 0 dx2 h2

Вне ямы (x<0; x>L):

d 2ψ + 2m [E −U0 ]ψ = 0 dx2 h2

Нас интересуют такие решения, для которых значения энергии E < U0, т.е. носители заряда локализованы в квантовой яме.

А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 7, стр. 8

Граничными условиями для решения уравнения Шредингера являются:

1.ψ (x) → 0 при x → ±∞ (волновая функция затухает под барьерами)

2.ψ (x) и dψ(x)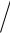dx непрерывны при x = 0, L

В области вне квантовой ямы уравнению Шредингера и 1-му граничному условию удовлетворяет функция вида:

ψ(x) = Aexp(m k2x) (“-“ для х > L и “+” для х < 0)

Подставляя эту волновую функцию в уравнение, получаем что k2 (волновой вектор) должен удовлетворять условию:

А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 7, стр. 9

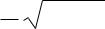
В области квантовой ямы уравнению Шредингера удовлетворяет функция вида:

ψ(x) = Bsin(k1x +δ)

Подставляя в уравнение получаем условие для волнового вектора k1

k1 = h1 2mE

Значение энергии и фазовый сдвиг δ будут определены из 2-го граничного условия.

А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 7, стр. 10