
Лекции по гетеропереходам / курс лекций физика и технология полупроводниковых наноструктур / 10_критическая толщина
.pdfФормирование дислокаций несоответствия и критическая толщина
Толщина напряженного слоя, при которой происходит формирование дислокаций несоответствия, снимающих упругое напряжение, называется
критической толщиной, hC.
Модель, позволяющая численно описать критическую толщину, была впервые предложена Матьюсом и Блэксли в 1975 г, модель механического равновесия.
Модель механического равновесия базируется на предположении, что в структуре уже имеются прорастающие дислокации (линии дислокаций направлены перпендикулярно или под углом к плоскости интерфейса).
А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 10, стр. 1
Под действием сил, действующих на дислокацию в напряженном слое, происходит загиб дислокации в плоскости интерфейса, т.е. образование дислокации несоответствия.
FE – сила, действующая на прорастающую дислокацию в напряженном слое вследствие напряжения рассогласования.
FL – сила, обусловленная изгибом линии дислокации, направленная в противоположную сторону
А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 10, стр. 2

Докритическая толщина
h<hC |
|
|
|
|
|
F |
|
|
|
F |
|
|
|
||||
|
L |
|
|||
|
|
|
|
|
E |
|
|
|
|
|
|
|
Критическая толщина |
|
h=hC |
FL |
FE |
А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 10, стр. 3 |
||

Из критерия механического равновесия, критическая толщина дается условием равенства сил, действующих на дислокацию:
FE = FL
F = |
|
1 |
bεYh |
|
|
|
|
||
E |
2 |
C |
|
|
|
|
|
||
F = |
|
|
Gb2 |
(1−ν 4)ln(h b) |
L |
4π(1−ν) |
C |
||
где b – вектор Бюргерса прорастающей дислокации,
ε – абсолютная величина двухосного напряжения, определяемая различием постоянных решеток,
G – модуль сдвига, Y – модуль Юнга, ν – отношение Пуассона (С12/(С11+С12)).
А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 10, стр. 4
Учитывая связь между модулями упругости, Y = 2G(1+ν) /(1−ν), получаем финальное уравнение модели Мэтьюса и Блэксли:
|
1−1/ 4ν |
1 |
|
||
hC/b |
|
|
|
|
[ln(hC/b)+1] |
4π(1 |
|
ε |
|||
|
+ν) |
|
|||
Это трансцендентное уравнение устанавливает связь между критической толщиной напряженного слоя и величиной рассогласования постоянных решеток (ε = d0 d −1).
Постоянная решетки твердого раствора AXB1-X связана с его химическим составом, x, законом Вегарда:
d AX B1−X C = xdAC +(1− x)dBC
А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 10, стр. 5
Таким образом, установлена с между критической толщиной и химическим
составом полупроводникового эпитаксиального слоя. |
|||||
|
1000 |
|
|
|
|
|
|
|
|
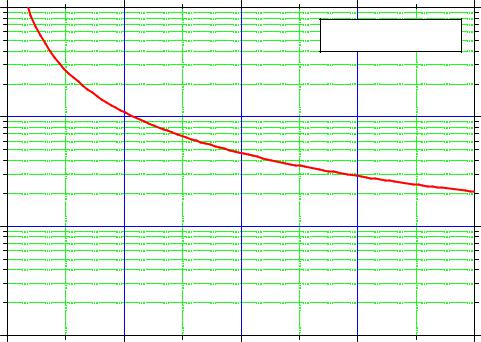
InXGa1-XAs/GaAs |
|
, МС |
100 |
|
|
|
|
толщина |
|
|
|
|
|
|
|
|
|
|
|
Критическая |
10 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
0.0 |
0.1 |
0.2 |
0.3 |
0.4 |
|
|
|
Мольная доля InAs |
|
|
Расчет критической толщины для InGaAs на GaAs.
А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 10, стр. 6
Недостатки теории механического равновесия:
1.Сложность учета всех сил, действующих на линию дислокации (например, силу трения решетки, возникающую при изгибе дислокации).
2.Для формирования дислокации несоответствия, обязательно должны быть прорастающие дислокации.
3.Неоднозначность результата при учете верхнего интерфейса квантовой ямы (обратный загиб линии дислокации приводит к удвоению силы FL, в результате критическая толщина оказывается в несколько раз выше).
4.Невозможность описать формирование новых прорастающих дислокаций и их сосуществование с интерфейсными дислокациями.
А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 10, стр. 7

InGaAs
GaAs
прорастающие дислокации 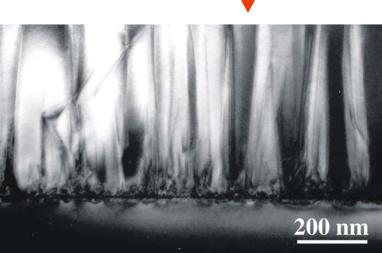
 дислокацииинтерфейсные
дислокацииинтерфейсные
Изображение методом просвечивающей электронной микроскопии слоя
InGaAs (x~20%) на GaAs. Осаждение методом МПЭ, 500С.
А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 10, стр. 8

Визуализация прорастающих дислокаций с помощью травления (EPD)
Например, электролитическое травление в растворе NH4OH:H2O2:H2O. Разные скорости травления для разных кристаллографических плоскостей приводят к растравливанию ямок в местах выхода дислокационных линий на поверхность.
А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 10, стр. 9
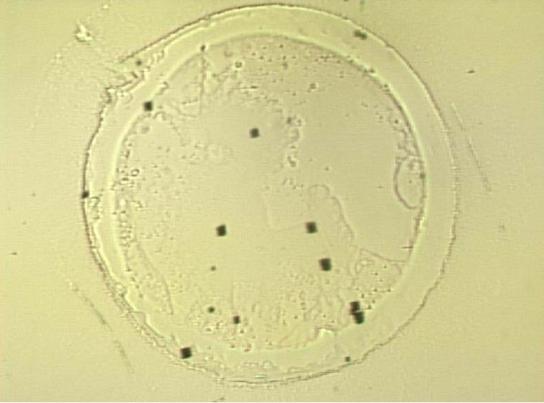
Темные точки – ямки травления подложки GaAs. EPD ~ 1000 см-2
А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 10, стр. 10
