Лекции по гетеропереходам / курс лекций физика и технология полупроводниковых наноструктур / 12_КЯ лазеры

Плотность состояний в системах с пониженной размерностью, Лазеры на квантовых ямах

Вобщем случае функция плотности состояний (ФПС):

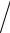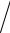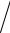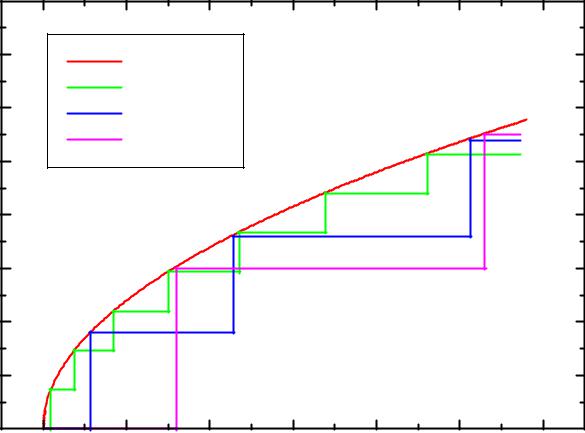
ρ(E)= (1V )(dNdE)= (1V )(dN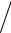dk )(dk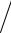dE)

При понижении размерности системы происходит изменение плотности состояний в пространстве волновых векторов и изменение дисперсионного соотношения. Рассмотрим это на примере перехода от объемного (3D) кристалла к 2D-квантовой яме.

А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 12, стр. 1

Дисперсионное соотношение

Объемный материал

где i- номер подзоны (уровня размерного квантования в квантовой яме) Ei – энергия квантового уровня

А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 12, стр. 2

Объем области k-пространства

Объемный материал

Ωk = 43πk3 (шар)

Квантовая яма

Ωk =πk 2 (круг)

Объем k-пространства, приходящийся на одно разрешенное состояние волнового вектора

Объемный материал

ωk = (2π)3/V, где V – объем кристалла Квантовая яма

ωk = (2π)2/S, где S – площадь квантовой ямы

А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 12, стр. 3

Число разрешенных электронных состояний

(в слое dk вблизи k)

Объемный материал

Квантовая яма dN = Skπ dk

А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 12, стр. 4

Плотность состояний

Объемный материал

Квантовая яма

где Θ(E – Ei) – функция-ступенька

Θ(E – Ei)=1 при E > Ei Θ(E – Ei)=0 при E < Ei;

А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 12, стр. 5

Поскольку полупроводниковый лазер характеризуется вертикальным транспортом носителей заряда и типично имеет в пределах активной области почти однородные макроскопические характеристики, в качестве меры накачки активной области обычно используется (поверхностная) плотность тока, а не его абсолютное значение. Соответственно, более важной характеристикой активной области является поверхностная плотность состояний (мэВ-1см-2), а не объемная (мэВ-1см-3), т.е. число доступных состояний на единицу площади, а не объема активной области:

здесь nQW – число квантовых ям

А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 12, стр. 6

Переход от узкого объемного полупроводника к квантовой яме

Quantum level, n

Возбужденные уровни в квантовых ямах Al0.3GaAs/GaAs

А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 12, стр. 7

E, meV

Переход 2D-плотности состояний в 3D при увеличении ширины квантовой ямы за счет добавления ступенек возбужденных подзон

А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 12, стр. 8

Найдем плотность состояний широкой квантовой ямы на энергии, отвечающей n-му уровню размерного квантования:

Уровень энергии

En ≈ π2h2 n2 2mL2

(приближение ямы с бесконечно высокими барьерами хорошо работает для широких ям)

Отсюда находим число подзон N, расположенных ниже

n ≈ 2mEn πLh

Высота одной ступеньки плотности состояний

ρ0 = m 1 , что соответствует примерно 1010 мэВ-1см-2/L

πh2 L

А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 12, стр. 9

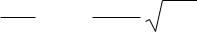
Плотность состояний широкой квантовой ямы на энергии, отвечающей n- му уровню размерного квантования

Таким образом, плотность состояний объемного материала является огибающей для ФПС квантовой ямы, содержащей несколько уровней размерного квантования.

А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 12, стр. 10