12.1. Рівняння стану реального газу. Ізотерми реального газу.

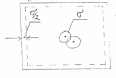
Для отр. р-ня стану реального газу, в р-ня стану ідеального газу введемо поправки, що врах. дію сил притягання і відштовхування між мол. Розглянемо 1 моль газу, який знах. в посудині кубічної форми. Нехай ефективний діаметр мол. – σ. Мол. може наблизитись до стінки на σ/2. Доступний для перебування в цій посудині

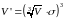
Наявність в V інших мол. газу робить також недоступним V для знах. центру розглядуваної мол.: , де

В процесі хаотичного руху мол. сфери їх “недоступності” в об’ємі перекриваються, тому праву частину виразу треба зменшити в 2 рази: - поправка Ван-дер-Ваальса на власний об’єм, тоді:

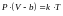
Врахуємо тепер дію сил притягання між мол. газу. Нехай сили притягання між мол. суттєві тільки на відстані R, яку наз. радіусом міжмолекулярної взаємодії.

Виділимо біля стінки посудини шар товщиною < 2R. Всі мол., що знах. на відстанях менших за R зазнають дії нескомпенсованої сили притягання зі сторони інших мол. газу, яка направлена від стінки посудини. . Від чого залежить величина ΔP? Очевидно, що F_{результ.}, що діє на кожну мол. шару товщиною d ~ n₀. В свою чергу , тобто поправка на тиск ΔP визначається сумою сил, що діють на мол. в шарі товщиною d біля стінки площею ΔS. , а – постійна Ван-дер-Ваальса, що врах. дію сил притягання між мол. реального газу. Її значення різне для різних сортів газу. – рівняння Ван-дер-Ваальса для одного моля газу. Тут входить молекулярний об’єм V, який в загальному випадку: . Тоді 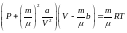- для к-ті газу. . a і b залежать як від сорту газу, так і від T і V, а тому р-ня є наближеним, бо a і b вважаються постійними. Це привело до того, що крім рівняння Ван-дер-Ваальса, існують ще інші рівняння стану реального газу: Рівняння Дітерічі: Рівняння Клаузіуса: .

Р-ня стану реального газу це р-ня 3-го степеня відносно V, а тому, якщо розгул. випадок T=const, кожному значенню P буде відповідати 3 різні значення V. Якщо побудувати залежність P(V) при T=const, то отр. ізотерму Ван-дер-Ваальса для реального газу. Якщо розглядати експерт. побудовані ізотерми реального газу (ізотерми Ендрюса), то для різних значень T вони виглядають.

Протяжність горизонтальної ділянки зменшується з ростом Т. І при деякій Т горизонтальна ділянка на ізотермі Ендрюса зникає. Цю Т наз. критичною. На представленому графіку можна виділити 4 області. В 1-ій області речовина перебуває в газоподібному стані, в 2 при кожній Т завжди має місце динамічна рівновага між рідиною та її парою, в 3 області речовина знах. в рідкому стані, в 4 області речовина знах. в критичному стані.

7.Внутрішня енергія реального газу. Зміна температури реального газу при його адіабатичному розширенні, ефект Джоуля-Томсона.

8.Вільна поверхнева енергія рідин. Додатковий тиск Лапласа. Капілярні явища.

Аналізуючи стан мол. рідини в поверхневому та глибинних шарах відмітимо, що на мол. поверхн. шару діють результуючі сили зі сторони інших мол., які напрямлені перпендикулярно до поверхні рідини. Мол. поверхн. шару отр. надлишкову Е, яку наз. поверхневою. В глибинних шарах дія мол. скомпенсована. Щоб збільшити площу вільної поверхні рідини необхідно, щоб сторонні сили виконували роботу проти нескомпенсованих сил δА_{ст. с} =σdS це σ- коєфіцієнт пропорційності. З закону збереження Е ця робота буде йти на зміну вільної поверхневої Е: dU= δА_{ст. с} = σ*dS повна вільна поверхнева енергія U= σS, S- площа вільної поверхневої рідини, σ- коєфіціент поверхневого натягу σ=δA/dS [Дж/м²]- чисельно рівна роботі, яку потрібно виконати для збільшення вільної поверхні рідини на 1 при T=const.

В поверхневому шарі мол. рідини завжди діють сили які, перешкоджають збільшенню площі вільної поверхні. Ці сили напрямлені до поверхні їх наз. силами поверхневого натягу.

Із-за дії сили поверхневого натягу на рідину відбувається викривлення поверхні рідини, ств. додатковий р – р Лапласа.

Капіляром наз. трубки малих розмірів в яких форма рідини в них міститься виникає основному силами взаємодії молекул між собою та з молекулами су-мішок а недіють сили тяжіння. Ід сил тяжіня поверхня рідини в трубках є горизон-тальною при занурені капілярів в посудену з рідинами спостерігається порушення закону сполучених посуден тобто рівні води в капілярах неспівпадають з різними рідинами в посудені в випадку змочуваню в капілярі піднімається више зазначе-ного рівня а в випадку незмочуваня капіляру знаходиться нижче зазначеного рів-ня рідини в посудені. Знайдемо співідношення для розрахунку висоти рідини в ка-пілярі в випадку часткового змочування.

Рідина в капілярі буде підніматись до тих пір доки тиск Лапласа

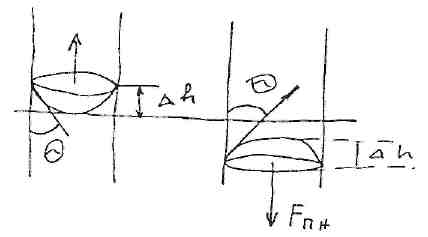
P_л = 2Ө/R не зрівноважелись з гідростатичним тиском Р= ρgh; Р_л = ρgh; h=2σ*cosӨ/ ρgh_к

9.Рідкі розчини, масова та молярна їх концентрації. Закони Рауля та Генрі для різних розчинів.

10.Типи міжатомної взаємодії в кристалах. Кристалічна ґратка. Дефекти в кристалах.

Якщо порівнювати тв. тіла за їх фіз.. власт. та аналізувати природу сил між мол. взаємодії, то виділяють 4 основні типи між мол. зв’язків: взаємодія Ван-дер-Ваальса, іонний зв’язок, ковалентний зв’язок, металічний зв’язок.

Ван-дер-Ваальсівська взаємодія має місце у всіх тв. тілах, але визначальною вона є в кристалах інертних речовин. По своїй природі є дипольною взаємодією і виникає між ел. нейтральними атомами. Іонний зв’язок є характерним для металів 1 групи, у яких на зовн. оболонці лише 1 електрон, який х-зується дуже слабким зв’язком цього електрону із атомним залишком. У атомів елементів 7 групи на зовн. електронній оболонці до повного “заповнення” не вистачає 1 електрона, і вони легко приймають лишній електрон для формування стійкої електронної групи, перетворюючись при цьому в негативний іон. Прийняття чи віддача атомом електрона приводить до перетворення атома у відповідним чином заряджений іон, і між іонами виникає значна кулонівська взаємодія. Іонні кристали х-зуються великою Е зв’язку (високі Т плавлення), а в механічному відношенні вони х-зуються високою міцністю і твердістю. Якісною х-кою ковалентного зв’язку є усуспільнення зовнішніх електронів двома або більшим числом атомів з утв. стійких електронних груп. Найбільш чітко утв. ковалентного зв’язку проявляється у речовин 4 групи. Кристали з ковалентним типом зв’язку в більшості за нормальних умов – діелектрики, у них також значні Т плавлення, х-зуються твердістю і міцністю. В атомів металів на зовнішній електронній оболонці міститься мала к-ть електронів, якої недостатньо для утв. ковалентного зв’язку і при чому ці електрони слабо взаємодіють з атомним залишком, через що вони можуть легко покидати межі атомів. В металах не може існувати також іонний зв’язок, бо всі іони одного знаку. Утв. відбувається завдяки взаємодії вільних електронів металу (електронний газ) із (+) зарядженими атомними залишками. Оскільки до металів відносяться елементи 1-3 групи, як 1-валентні так і 3-валентні, то різною для різних металів є Е зв’язку, Т плавлення, як і механічні властивості суттєво різняться.

Під атомним рядом розуміють напрям в кристалічному тілі, в якому розташовується дуже велике число атомів. Атомна площина – площина виділена в тв. тілі в якій розташовується дуже велике число атомів. Під кристалічною граткою розуміють просторово-періодичну структуру, яка утворилася при перетині всеможливих атомних рядів у тв. тілі. Для того, щоб описувати положення вузлів кристалічної гратки виберемо відповідну кристалографічну с-му координат. Її вибираєм так, щоб симетрія системи координат mах відтворювала симетрію кристадічної речовини. В такій системі координат положення атома А буде задавати радіус-вектор . a,b,c – вектори трансляції, а їх модулі – періоди гратки. Паралелепіпед побудований на векторах трансляції наз. елементарною коміркою.

Дефекти в кристалах

В монокристалічних тілах існує дальній порядок в розташуванні атомів. Проте в реальних монокристалах завжди існують такі області, в яких порушується періодичність в розташуванні атомів. Такі області наз. дефектами. В залежності від розмірів дефектних областей проводять їх класифікацію.

Точкові дефекти – розміри яких співрозмірні з розмірами атомів в 3 взаємоперпендикулярних напрямках.

Лінійні – у двох напр. співрозмірні, а в третьому >>

Плоскі – в 1співрозмірні, а в 2-х >>

Об’ємні – у всіх 3 рапрямках дефект >> за розміри атома

До точкових дефектів відносять: вакансії – місця, де згідно дальнього порядку повинен бути атом, але він відсутній; атоми заміщення – у вузлі гратки, де повинен знаходитися атом одного сорту, знаходиться атом іншого сорту; атоми втілення – атоми, які знаходяться в місцях ”не передбачених” дальнім порядком.

Вакансії відіграють одну з основних ролей при протіканні дифузійних процесів в тв.тілах, вони є термодинамічно рівноважними дефектами. Поблизу точкових дефектів має місце зміщення сусідніх атомів із рівноважних положень

До лінійних дефектів відносяться в основному крайові і гвинтові дислокації. Крайову дислокацію можна розглядати як лінію обриву атомної площини в кристалі. Значні порушення в розташуванні атомів мають місце издовж “лінії обриву”.

Поверхневі деформації утв. в основному в процесі отримання кристалічних матеріалів, і інколи при механічній дії на кристал.

До об’ємних дефектів відносяться: включення іншої фази, мікропори, мікротріщини. Мікропори і включення іншої фази утворюються в кристалах в процесі їх вирощування, а мікротріщини – при механічній дії на кристал.

11.Фазові перетворення 1-го та 2-го роду. Рівняння Клайперона-Клаузіуса. Фазова діаграма. Потрійна точка.

Зміна складу речовини яка супроводжуються різними змінами деяких власт. чи параметрів наз. фазовим перетворенням.

Розрізняють фазові переходи 1–го і 2–го роду. Фазові перетв. 1-го роду наз. зміну стану системи, яка супроводжується зміною внутрішньої Е. (плавлення, пароутворення, сублімація). Фазові перетв. 2–го роду наз. зміну стану речовини, яка супроводжується зміною Т величин зв’язаних з похідною від Е по Т (σ,χ). Фазові перетв.2–го роду відбув. тільки в тв. тілах за винятком рідкого Не, який при T=const переходить у надтекучий стан.

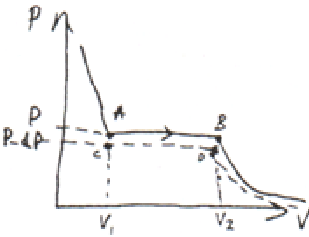
Ізотерми реального газу дозволяють отр. рівняння Клайп– Клауз.

Розгл. ізотерму Ендрюса побудовану для к-ті моль речовини і розгл. в якості початкової с–ми с-му, що відповідає т.А, тобто стану в якому вся речовина знах. в рідкому стані і над нею відсутня насичена пара. При повільному збільшені об’єму рухаючи поршнем при T = const тут буде відбув. перетв. рідини в газоподібний стан і поки вона переходитиме в цей стан, буде забирати від нагрівника теплоту Q_затр = υL, L- молекулярна теплота пароутв. В т.В від’єднаємо с–му від нарівника і проведемо незначне адіабатне розширення газу до точки С, при цьому р зменшиться на dP і стане P-dP в об’ємі V – dV, а температура T – dT і проведемо зменшення об’єму до стану D, з якого адіабатичним стисненням її можна перевести в точковий стан А.

Тут замкнутий процес ABCD представляє цикл Карно і визначити його ККД можна двояко з одного боку η = dT/T з іншого η = A_ц /Q_зат

Роботу за циклом знайдемо як фігуру обмежену лініями циклу

А_ц = (V₁–V₂)dp η = (V₁–V₂)dp/ Q_зат = (V₁–V₂)dp/L,

V₂ = υ₂ /υ, V₁ = υ₁ /υ молярний обєм відповідно V₂ – класична пара та V₁ – рідини при температурі Т. (V₁–V₂)dp/L = dT/T,

dP/dT = 1/T(V₁–V₂), рів. Клайп – Клауз визначає зміну тиску насиченої пари із зміною Т. Часто його записують в іншому вигляді dP/dT = Т*(V₁–V₂)/L виражає зміну Т фазового перетв. речовини із зміною тиску причому вони є універсальними і нами розгул. для різних фазових перетворень.

Кристалізація – процес переходу речовини з рідкого у тв. стан. Відбув при T=const і супроводжується виділенням певної к-ті тепла Q_кр = λw, λ - густина питомої кристалізації. λ = Q_кр / w, показує яка к-ть теплоти виділяється при кристалізації маси речовини.

Плавлення – це процес переходу речовини з тв. стану в рідкий. Плавлення кристалічної речовини відбув. при T=const Т_пл = Т_кр . Для протікання процесу плавлення до речовини потрібно підводити певну к-ть теплоти. Ця теплота витрачається на збільшення к-ті степенів вільності.dT/dP = T(V_тв –V_р), Т плавлення змін. із зміною зовнішніх парам. Ці зміни описуються рів. Клайперона – Клаузіуса. Якщо побудувати залежність Т плавлення від зовнішнього тиску то утв. характернана крива, яка / діаграму на обл. газоподібної, рідкої та тв. фази. Проаналізуємо перехід речовини з рідкого в газоподібний стан. Обидві криві на РТ діаграмі переміщуються в т.А, в якій одночасно можуть існувати 3 речовини ця т. наз. потрійною точкою.

12.Дифузія в газах. Закони Фіка. Коефіцієнт дифузії при стаціонарній дифузії.

Дифузія газів. Закони Фіка. Коефіцієнт дифузії при стаціонарній дифузії.

Процес дифузії полягає у вирівнюванні густини чи складу газу. Якщо процес дифузії розглядається в однорідному середовищі, то в ньому беруть участь лише однакові молекули, і цей процес називається самодифузією. Якщо в процесі дифузії відбувається вирівнювання концентрацій різних компонент системи, то цей процес називається (взаємною) дифузією.

В процесі дифузії створюються потоки молекул із області вищої в область нижчої концентрації в сторону максимального зменшення концентрації. Чисельно дифузійні потоки характеризуються величиною

(1) або

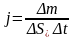(2)

Дифузійні потоки завжди приводять до зменшення різниці концентрації, яка їх викликала. В замкнутій системі відбувається врівноваження концентрації, тобто нестаціонарна дифузія. Дифузія, при якій різниця концентрацій в системі не змінюється, називається стаціонарною, для якої необхідна дія сторонніх факторів.

Експериментально встановлено, що дифузійний потік пропорційний градієнту концентрації. Це – перший закон Фіка:

(3), х – напрямок максимальної зміни концентрації

(3) описує процес стаціонарної дифузії, коли . Згідно (3) можна знайти миттєве значення дифузійного потоку протягом малого інтервалу часу , за який градієнт концентрації можна вважати незмінним. При нестаціонарній дифузії градієнт концентрації зменшується з часом.

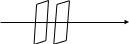
n₁ n₂ х

n₁>n₂

x x+dx

При нестаціонарній дифузії:

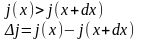(4)

йде на збільшення концентрації молекул в області між перерізами. Вважаємо dx малим і незмінним: . Тоді, враховуючи означення дифузійного потоку, запишемо

(5)

Представимо j(l+x) через зміну градієнта концентрації з відстанню

(6)

(7)

Прирівнявши з (5) і (7), отримаємо:

(8) – другий закон Фіка, який пов’язує швидкість зміни концентрації з часом із зміною градієнта концентрації з відстанню.

Розглянемо посудину з газом, в об’ємі якої концентрація не однакова, а змінюється так, що в будь-якій площині, перпендикулярній до певного напрямку(осі ОХ), концентрація має однакове значення. Зміна концентрації можлива лише вздовж вибраного напрямку.

n=f(x) (9)

N₁

n₁ N₂ n₂ x

n₁>n₂

Виберемо площадку площею S, перпендикулярну до осі ОХ. За однаковий малий проміжок часу dt число молекул, які пройдуть крізь неї, не буде рівним у взаємно протилежних напрямках (N₁>N₂), оскільки концентрація молекул по різні боки різна. Виділимо перерізи, що знаходяться від розглянутої площадки на відстані по обидві сторони. Позначимо концентрації в цих перерізах та .

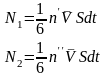(10)

- об’єм, з якого молекули переходять через площадку.

Визначимо величину дифузійного потоку.

(11)

(12)

(13)

(14)

Порівнюючи (14) з першим законом Фіка (3), отримаємо:

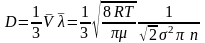(15) – коефіцієнт стаціонарної дифузії

13.Теплопровідність, закон Фур’є для теплопровідності. Механізми протікання теплопровідності в різних речовинах.