30. Конденсатор в колі синусоїдного струму.

Якщо прикладена до конденсатора напруга не змінюється в часі, то заряд на одній з його обкладинок і заряд – на іншій ( – ємність конденсатора) незмінні і струм через конденсатор не проходить Якщо ж напруга на конденсаторі змінюється в часі, наприклад за синусоїдальним законом (рис. 30.1, а):

(30.1)

то за синусоїдальним законом буде мінятися і заряд конденсатора: – і конденсатор буде періодично перезаряджатися. Періодична перезарядка конденсатора супроводжується протіканням через нього зарядного струму

(30.1’)

Додатній напрям струму через конденсатор на рис. 30.2, а співпадає з додатнім напрямом наруги. Із співставлення (3.19) і (3.19’) видно, що струм через конденсатор випереджає по фазі напругу на конденсаторі на 90°. Тому на векторній діаграмі рис. 30.1, б вектор струму випереджає вектор напруги на 90°. Амплітуда струму рівна амплітуді напруги поділеній на ємнісний опір:

(30.2)

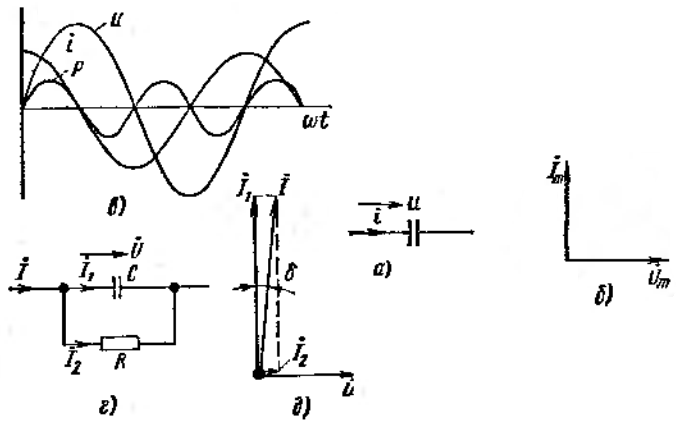
Рис. 30.1

Дійсно,

(30.3)

Ємнісний опір обернено пропорційний частоті і вимірюється в омах. Графік миттєвих значень зображені на рис. 30.1, в.

Миттєва потужність

(30.3)

За першу чверть періоду конденсатор споживає від джерела живлення енергію, яка йде на створення електричного поля в конденсаторі. В другу четверть періоду напруга на конденсаторі зменшується від максимуму до нуля, і занесена в електричне поле енергія віддається джерелу (миттєва потужність від’ємна). За третю четверть періоду енергія знову запасається, за четверту віддається і т. д.

Якщо про інтегрувати за часом обидві частини рівняння

(30.4)

то отримаємо

(30.5)

Рівняння (30.5) дозволяє знайти напругу на конденсаторі через струм на конденсаторі.

При викладі питання про проходження синусоїдального струму через конденсатор передбачалося, що діелектрик, що розділяє пластини конденсатора, є ідеальним і ньому немає втрат енергії. Однак при прикладені синусоїдальної напруги до пластин конденсатора, розділених твердим, або рідким діелектриком, в останньому завжди є деякі втрати енергії, зумовлені в’язким тертям при повороті дипольних молекул, а також недосконалістю діелектрика (наявністю невеликої провідності). Ці втрати відносно малі, і ними часто можна знехтувати. Якщо вимагається врахувати їх в розрахунку, то конденсатор заміняють схемою заміщення (рис. 30.1, г). В цій схемі паралельно ємності приєднано активний опір втрати енергії в якому імітують втрати енергії в реальному діелектрику.

Струм через конденсатор рівний геометричній сумі двох струмів: струму через ємність, який на 90° випереджує напругу на конденсаторі (рис. 30.1, д), і відносно малого за величиною струму через активний опір який співпадає по фазі з напругою .

Таким чином, струм через конденсатор з неідеальним діелектриком випереджає напругу на кут, трохи менший 90°. Кут який утворює струм зі струмом , прийнято називати кутом втрат. Він залежить від сорту діелектрика і частоти і рівний в кращому випадку кільком секундам, в гіршому – кільком градусам. Величина подається в таблицях, які характеризують властивості різних твердих і рідких діелектриків. Величину називають добротністю конденсатора.