20. Середнє і діюче значення синусоїдно змінної величини.(3.2)

Під середнім значенням синусоїдно змінної величини розуміють її середнє значення за півперіода. Так, середнє значення струму

Тобто середнє значення синусоідального струму складає 2/π=0,638 від амплітудного. Аналогічно,

Широко застосовують поняття діючого значення синусоідально змінної величини(його називають також ефективним або середньоквадратичним). Діюче значення струму

Слідуючи з цього,діюче значення синусоідального труму рівно 0,707 від амплітуди. Аналогічно,

Можна співставити теплову дію синусоідального струму струм з тепловою дією постійного струму , що тече в цей же час по цьому ж опору.

Кількість тепла,що виділяється за один період синусоїдальним струмом :

Виділене за той же час постійним струмом тепло рівне .Прирівняємо їх:

Таким чином, діюче значення синусоїдального струму І чисельно рівне значенню такого постійного струму,який за час,рівний періоду синусоїдального струму,виділяє таку ж кількість тепла,що і синусоїдальний струм.

Більшість вимірювальних приладів показує діюче значення вимірюваної величини)

21. Коефіцієнт амплітуди і коефіцієнт форми.(3.3)

Коефіцієнт амплітуди - це відношення амплітуди періодично змінної функції до її діючого значення. Таким чином, для синусоїдального струму :

Під коефіцієнтом форми розуміють відношення діючого значення періодично змінної функції до її середньому за півперіода значенню.Для синусоїдального струму :

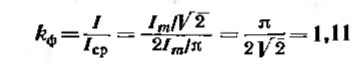
(для несинусоїдальних періодичних струмів , Це відхилення досить точно показує, наскільки несинусоїдальний струм відрізняється від синусоїдального.)

Іноді користуються поняттям коефіцієнта форми несинусоідальної функції,що оприділяється наступним чином:

Де - середнє по модулю значення струму

22. Зображення синусоїдно змінних величин векторами на комплексній площині.(3.4)

На рисунку 3.2 дана комплексна площина, на якій можна зобразити комплексні числа. Комплексне число має дійсну(основну) і уявну частини. По осі абсцис комплексної площини відкладають дійсну частину комплексного числа,а по осі ординат – уявну частину. На осі дійсних значень ставимо +1, а на осі уявних значень +j( ). З курсу математики відома формула Ейлера

Комплексне число зображають на комплексній площині вектором,чисельно рівним одиниці і зіставними кутом α і віссю дійсних значень (віссю +1). Кут α відраховуєм проти часової стрілки від осі +1. Модуль функції :

Проекція функції на вісь +1 рівна cos α , а на вісь +j рівна sin α . Якщо замість функції взяти функцію , то

На комплексній прощині ця функція, так же ж як і функція буде зображена під кутом α до осі +1, але величина вектора буде в раз більша.

Кут α в формулі (3.8) може бути любим. Припустимо, що α= , тобто кут α змінюється прямо пропорційно часу. Тоді

Частина рівняння представляє собою дійсну частину (Rе) виразу :

А функція є коефіцієнт при уявній частині (Im)

виразу :

Таким чином, синусоїдально змінний струм і (3.1 і 3.10б) можна представити як Im ,або що те ж саме, як проекцію обертаючого ся вектора на вісь +j(рис. 3.3.):

Історично склалося так, що в радіотехнічній літературі за основу зазвичай застосовують не синусоїду, а косинусоїду,і тому користуються формулою (8.10а)

З ціллю однотипності прийнято на комплексній площині зображати вектори синуідально змінних в часі величин для моменту часу . При цьому вектор рівний :

Де - комплексна величина,модуль якої рівний , а кут, під яким вектор проведений до осі +1 на комплексній площині, рівний початковій фазі

Величину називають комплексною амплітудою струму і. Комплексна амплітуда зображає струм і на комплексній площині для моменту часу .