Модель третьего типа

Системе с кривой разгона третьего типа соответствует передаточная функция:

(26)

Представим структуру системы в виде последовательного соединения двух звеньев. Первое звено – реальное дифференцирующее, а второе – звено II-го порядка общего вида.

При подаче на вход первого звена единичного возмущения x(t)=1(t), выход звена , где δ=α₁b₁. Кривая разгона в этом случае является решением дифференциального уравнения:

(27)

Учитывая, что в точке перегиба(t=t_n) y^''(t_n)=0, уравнение (27) преобразуется к виду:

(28)

Интегрируя (27) в пределах от t₁=0 до t₂=∞, получим:

(29)

При интегрировании (27) от t₁=t_m до t₂=∞ будем иметь:

(30)

Из соотношений (29) и (30)находим:

(31)

а из (28) (29)получим

(32)

Решение системы из уравнений (31) и (32) даёт значения α₁ и b.

Если проинтегрировать уравнение (27) от точки перегиба кривой разгона до t=∞ , получим:

, откуда, учитывая (29)

; (33)

Исходные коэффициенты a_i вычисляются по формулам (5). Найденные коэффициенты проверяются решением дифференциального уравнения (27). Решение этого уравнения зависит от корней характеристического уравнения:

ar²+br+1=0.

При этом значение коэффициента с₁ одинаково для любого значения корней:

Варианты значений корней:

14. Вещественные неравные корни: r₁=α₂, r₂=α₃

где ;

(константы определены с учётом того, что все выкладки производились при нулевых начальных условиях: y(0)=0; y^'(0)=0)

15. Вещественные равные корни: r₁=r₂= -α₂

;

16. Комплексные корни:

;

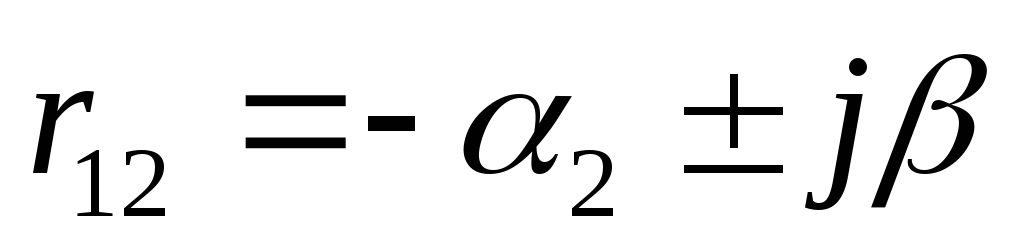
На основе изложенного метода идентификации моделей в виде дифференциального уравнения (передаточной функции) по кривой разгона можно установить следующую последовательность действий:

17. Определение принадлежности кривой разгона к одному из типов, рассматриваемых в методике.

18. Для всех кривых, кроме последнего типа устанавливается относительный масштаб по ординате, соответствующий y_уст=1 и вычерчивается приведенная кривая разгона.

19. По приведенной кривой разгона определяются значения:

t_n, t_m, y(t_n), y(t_m), y^'(t_n), S_0∞, S_n∞, S_m∞

20. Из соответствующих уравнений определяются значения α₁ и b.

21. Для кривых типа II и III определяются значения δ.

22. В зависимости от типа кривой по соответствующим формулам определяют коэффициент а.

23. Определяются коэффициенты дифференциального уравнения а₁, а₂, а₃ из соотношений (5). Для кривых типа II и III определяют значение b₁.

24. Определяются постоянные интегрирования в зависимости от типа.

25. Производится проверка с помощью графического построения, проверяется решение дифференциального уравнения.

6. Идентификация линейных динамических систем

1. Условия идентифицируемости линейных динамических систем

Рассмотрим задачу идентификации параметров математической модели, заданной в виде системы обыкновенных линейных дифференциальных уравнений

.

Состояние системы задается вектором x(t) n- мерного эвклидового пространства и известны путем измерений следующие векторы

(1)

Задача состоит в нахождении такой матрицы А, чтобы выполнялись условия

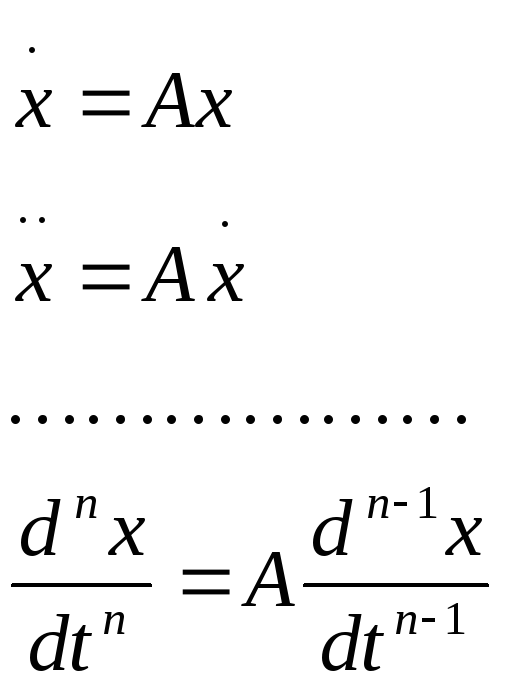(2)

Состояние системы, заданное известными векторами (1), назовем идентифицируемым, если для него существует матрица А, удовлетворяющая равенствам (2).

Систему уравнений (2) для каждой строки матрицы А

сложно записать систему уравнений:

для j =1,2,..., n (3)

Условие существования решения задачи идентификации, т.е. систем (3), можно записать в виде

(4)

Из соотношений (3) параметры модели можно определить по формулам

для j =1,2,..., n (5)

Подставим соотношения (2) в условие (4), получим неравенство

det (x, Ax, ... , A^n-1x) 0 (6)

Укажем на связь между задачами идентификации и управляемости. Эта связь формулируется так:

для существования решения задачи идентификации в виде математической модели

при наблюдении вектора состояния x(t) достаточно, чтобы матрица А и вектор x(t) удовлетворяли условия вполне управляемости

det (b, Ab, ... , A^n-1b) 0

где b = x(t).

Поскольку матрица А наперед неизвестна, то на практике условия идентификации проверяют на основании условия (4).

Для дискретных линейных систем управления определение идентифицируемости формулируется следующим образом: если по известным значениям векторов x(k), x(k+1), ... , x(k+n) состояние дискретной линейной стационарной системы n-го порядка

x(k+1) = Ax(k)

можно восстановить матрицу А, то систему называют идентифицируемой.

Теорема. Решение задачи идентификации дискретной линейной системы имеет место, если

det (x(k), x(k+1), ... , x(k+n-1)) 0