Дополнительный признак перпендикулярности прямых (теорема о трёх перпендикулярах)
№ 26 (устно). К плоскости прямоугольника ABCD проведен перпендикуляр СМ. Доказать, что прямая МD перпендикулярна прямой ВС.
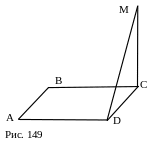План доказательства.
1. MD AD.
2. AD || BC.
3. Вывод.
№ 27. Катеты прямоугольного треугольника АВС равны 15 и 20. Из вершины прямого угла С проведён к плоскости этого треугольника перпендикуляр CD, равный 35. Найти расстояние от точки D до гипотенузы АВ.
Д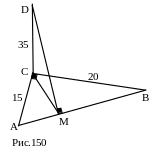
ополнительные
построения.
1.CD AB.
2. DM.
План решения
1. АВ.
2. СМ.
3. DM.
Ответ: 37.
№ 28. Стороны треугольника относятся как 10:17:21, а его площадь равна 84. Из вершины большего угла этого треугольника проведён перпендикуляр к его плоскости, равный 15. Найти расстояние от его концов до большей стороны.
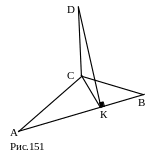Дополнительные построения.
Те же, что и задаче № 27.
План решения.
Стороны АВС
(используя формулу Герона).
2. СК.
3. DK.
Ответ: 8, 17.
№ 29 (устно). Из вершины А треугольника АВС проведён к его плоскости перпендикуляр AD. Из точки D опущен перпендикуляр на сторону ВС. При каких условиях этот перпендикуляр пройдёт через один из концов отрезка ВС?
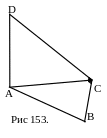
Ответ: если В=90 или С=90.
№ 30. Вне плоскости параллелограмма ABCD взята точка К, отстоящая от сторон АВ и DC параллелограмма на расстояния, равные КМ и КЕ. Доказать, что МЕ – высота параллелограмма.
Дополнительные построения.
КО ABCD.
ОЕ DC.
КЕ – заданное расстояние.
Аналогично КМ – заданное расстояние.
П
лан
доказательства
Доказать, что точки М, О, Е лежат на одной прямой.
2. Вывод.
№ 31. Через вершину В квадрата ABCD к его плоскости проведён перпендикуляр ВМ. Известно, что МВ = m, AB = n. Найти расстояние от точки М до сторон квадрата и до прямой АС.
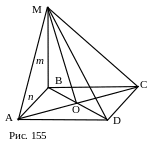План решения.
1. МВ – расстояние от точки М до
сторон АВ и ВС.
2. МВ = m.
3. МА – расстояние от точки М до
стороны AD.
4. МА.
5. МС – расстояние от точки М до
стороны DС.
6. МС.
7. МО – расстояние от точки М до стороны АС. 8. МО.
Ответ: МВ = т,
МА = МС =
,
МО =
.
№ 32 (устно). Существует ли четырёхугольная пирамида, у которой каждая боковая грань – прямоугольный треугольник?
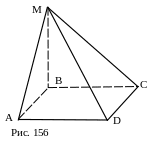
Ответ: существует. Это пирамида в основании которой лежит прямоугольник, в частности, квадрат, и одно из боковых рёбер перпендикулярно к плоскости основания (рис. 156).
№ 33. Из вершины А прямоугольника ABCD проведён к его плоскости перпендикуляр АМ, конец М которого отстоит от других вершин на расстоянии 6, 7 и 9. Найти длину перпендикуляра АМ.
План решения.
1. DC.
2. AM.
Ответ: 2.
№ 34. Основанием пирамиды служит квадрат, её высота проходит через одну из вершин основания. Определить боковую поверхность этой пирамиды, если сторона основания равна 20 см, а высота равна 21 см.
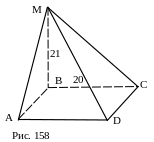
План решения.
1. Площадь МВС и АМВ.
2. МС.
3. Площадь МСD и МАD.
4. Площадь боковой поверхности
данной пирамиды.
Ответ: 1000.
№ 35. К плоскости квадрата ABCD проведён перпендикуляр ВР, равный 3 см. PD = 5см. Найти периметр треугольника АОС, где О – центр окружности, описанной около треугольника APD.
Д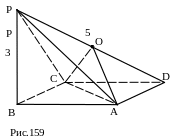
ано:
ABCD – квадрат, ВP^ABCD,
PD=5, BP=3,
О – центр oкружности, описанной около DAPD.
Найти: РDСОА.
План решения.
1. BD=AC. 2. Центр О – середина PD.
3. ОР. 4. ОР=ОА. 5.ОА=ОС. 6.РАОС . Ответ: 9.
№ 36. Основанием пирамиды служит равносторонний треугольник со стороной а. Одна из боковых граней также равносторонний треугольник и перпендикулярна к плоскости основания. Определить боковую поверхность этой пирамиды.
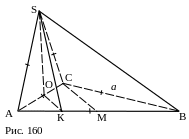
Построения.
SOAC.
2. M – середина AB.
3. OK || CM.
План решения.
1. SASC. 2. SOABC. 3. SK – высота ASB. 4. SO. 5. OK. 6. SK.
7. SASB. 8. ASB=CSB. 9. Sбоковой поверхности.
Ответ:
.
№ 37. Основанием пирамиды служит правильный шестиугольник со стороной а. Одно из боковых рёбер перпендикулярно к плоскости основания и равно стороне основания. Определить боковую поверхность этой пирамиды.
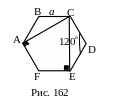
План решения.
1. Построения: СЕ FE, CA AF (рис.162).
2. SCD, SEF –прямоугольные (рис. 161)
3. Площадь SCD. 4. СЕ, SE, площадь SEF.
5. Построения: СК ED, SK (рис. 163, 164).
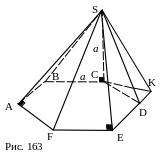
6. CK, SK, площадь SED. 7. SCD=SCB, SFE= SAF, SED=SAF.
8.Боковая поверхность пирамиды.
Ответ:
.
№ 38. Существует ли четырёхугольная призма, у которой сечение, проходящее через параллельные рёбра верхнего и нижнего основания – прямоугольник?
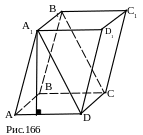
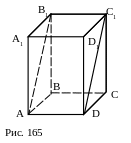
Ответ: существует. Это прямая призма, в основании которой лежит прямоугольник (квадрат). АВ1С1D – сечение – прямоугольник (рис. 165). Это наклонная призма, в основании которой лежит прямоугольник (квадрат) и две боковые грани перпендикулярны к плоскости основания (рис. 166).
№ 39. В правильной треугольной призме АВСА1В1С1 построить сечение, проходящее через точки А, М (А1М=МВ1), Р (ВР=РС). Найдите площадь сечения, если все рёбра призмы равны а.
П
лан
построения.
1. АМ.
2. АР.
3. MK || AP.
4. KP.
5. AMKP – искомое сечение.
П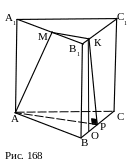
лан
решения.
1. Дополнительные построения.
Проведём КОВС.
2. АМКР – прямоугольная трапеция.
(Р=К=90).
3. АР. 4. МК. 5. ОР.
6. КР. 7. SAMKP.
Ответ:
40. Доказать, что диагональ куба и диагональ его грани, лежащие на скрещивающихся прямых, перпендикулярны.
П
лан
доказательства.
1. А1С – наклонная,
АС – её проекция на плоскость
нижнего основания куба,
2. АС BD.
3. Вывод.
4. Аналогично относительно
диагоналей А1С и DC1.
41. Доказать, что диагональ куба А1С перпендикулярна плоскости ВС1D.
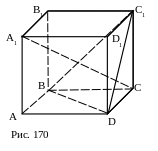
План доказательства.
1. А1С BD.
2. А1С DC1.
3. Вывод.
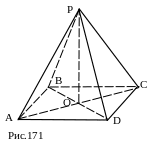
№ 42 (устно). Доказать, что диагональ основания правильной четырёхугольной пирамиды перпендикулярна её боковому ребру (рис. 171).
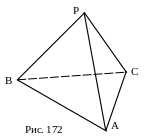
№ 43 (устно). Доказать, что сторона основания правильной треугольной пирамиды перпендикулярна её боковому ребру (рис. 172).
№ 44. В правильной треугольной пирамиде SABC сторона основания равна а и боковое ребро равно в. Провести в этой пирамиде плоскость через середины рёбер АВ и ВС параллельно ребру SB. Определить площадь полученного сечения.
П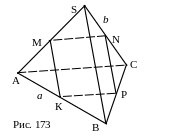
лан
построения сечения.
К, Р – середины АВ и ВС.
1. КР.
2. МК || SB.
3. PN || SB.
4. KMNP – искомое сечение. Доказать.
План решения.
1. KMNP – прямоугольник.
2. КР. 3. МК. 4. Площадь KMNP.
Ответ:
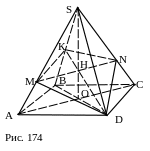
№ 45. Пусть SABCD – правильная четырёхугольная пирамида, у которой боковое ребро равно диагонали основания. Через вершину основания пирамиды провести сечение, перпендикулярное противолежащему боковому ребру.
План построения.
Точка К: ВК = KS.
DK.
Точка Н – пересечения DK и SO.
MN: HÎ MN, MN || AC.
DMKN – искомое сечение. Доказать.
№ 46. Основанием призмы является правильный треугольник, сторона которого равна а. Каждое боковое ребро призмы равно в, угол между одним из боковых рёбер и прилежащими к нему сторонами основания равен 45. Найти боковую поверхность призмы.
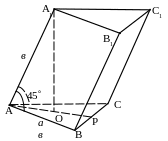План решения.
1. А1ОАВС, точка ОАР,
где АР – биссектриса А.
2. АА1ВС.
3. ВВ1С1С прямоугольник.
4.
.
5.
.
Рис. 175
Ответ:
III. Углы между прямыми и плоскостями
1. Теоретическая карта №3
1.1. Угол между прямой и плоскостью
Определение. Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и её проекцией на плоскость [5, с. 43], [10, с. 51 ].
Угол φ между прямой АВ и её проекцией ВО на плоскость α (рис. 176) является наименьшим из всех углов, которые данная прямая образует с прямыми, проведенными на плоскости через точку В.
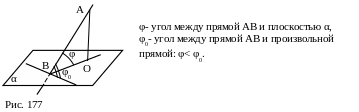
1. 2. Угол между плоскостями
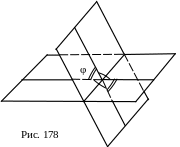
Определение 1. Две пересекающиеся плоскости образуют четыре двугранных угла с общим ребром (рис. 178). Если φ тот из четырёх углов, который не превосходит каждого из остальных, то говорят, что угол между пересекающимися плоскостями равен φ, Очевидно, что 0°< φ≤90° [5, с.48].
Замечание.
Напомним, что двугранный угол измеряется линейным углом, который образуется, если отметить на ребре двугранного угла какую – нибудь точку и в каждой грани из этой точки провести луч перпендикулярно к ребру (рис. 179).
Покажем иные способы построения линейного угла.
Третий способ
План построения.
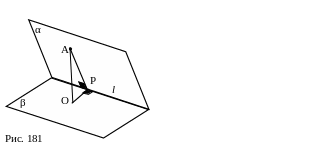
Определение 2. Пусть данные плоскости пересекаются (рис.182). Проведём плоскость, перпендикулярную их линии пересечения. Она пересекает данные плоскости по двум прямым. Угол между этими прямыми называют углом между данными плоскостями [10, с. 52].
