2.6. Дополнительные признаки перпендикулярности плоскостей

Приведём доказательство второго дополнительного признака перпендикулярности плоскостей.

Д оказательство

1. Существует прямая а:

2. Проведем плоскость t: и пересекает плоскость β по прямой в.

3. Так как , то а || в, но тогда , следовательно,

3. Задачи к теоретической карте №2

3.1. Перпендикулярность прямых

№ 1 (устно). Стороны четырёхугольника ABCD и прямоугольника A₁B₁C₁D₁ соответственно параллельны. Доказать, что ABCD – прямоугольник.

№ 2 (устно). Дан параллелепипед ABCD A₁B₁C₁D₁. Доказать, что

1) CD В₁C₁ и AB A₁ D₁, если ÐBAD=90°.

2) AB^CC₁ и DD₁^A₁B₁, если AB^DD₁.

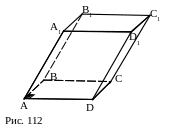
№ 3 (устно). В тетраэдре DABC ВС^AD. Доказать, что AD^MN, где M и N – cередины рёбер AB и АC.

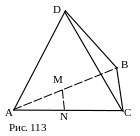
№ 4 (устно). РАВСD – правильная пирамида, Q – центр её основания. Как построить прямую, проходящую через точку Р и перпендикулярную прямой 1) AD; 2) AC; 3) PQ? 4)Как построить прямую, проходящую через точку К – середину ребра AD, перпендикулярно PQ? Рассмотреть решения для

случая пересекающихся и скрещивающихся перпендикулярных прямых. О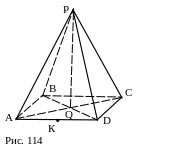 тветы обосновать.

Ответы.

1) PK; прямая l:

2) PQ; прямая p:

3) прямая п:

4) KQ; прямая

3.2. Перпендикулярность прямой и плоскости.

№ 5 (устно). ABCDA₁B₁C₁D₁ – куб. Как построить прямую, которая проходит: 1) через точку С и перпендикулярна прямой С₁D; 2) через точку С₁ и перпендикулярна прямой BD? Ответы обосновать.

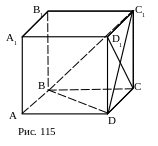
Ответы.

1)CD₁C₁D; BCC₁D.

2) C₁OBD; C₁CBD.

№ 6. Если даны две прямые такие, что одна из них параллельна, а другая перпендикулярна к плоскости, то они перпендикулярны. Доказать.

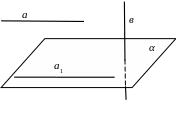
Дано:

Доказать:

План доказательства.

1. Существует прямая

2.

3

Рис. 117

.

№ 7. Точки А и В являются проекциями точки М на плоскости граней двугранного угла. Докажите, что прямая АВ перпендикулярна к его ребру.

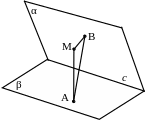План доказательства.

1. с  АМ, с  ВМ.

2. с  МАВ.

3. с  АВ.

Рис. 118

№8. Если две прямые перпендикулярны к одной и той же плоскости, то они параллельны. Доказать.

Доказательство приведено в учебниках [5, с. 36], [10, с. 29].

№ 9. Общая сторона АВ треугольников АМВ и АКВ лежит на данной плоскости. Проекции сторон АМ и АК на эту плоскость перпендикулярны АВ. Как расположены относительно друг друга АВ и плоскость МАК?

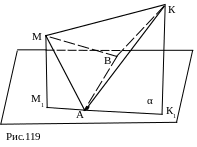План решения.

1. Точки М₁, А, К₁ принадлежат

одной прямой.

2. Точки М₁, М, К, К₁

принадлежат одной плоскости α.

3. АВ  α.

4. АВ  МАК.

№ 10. Дан квадрат ABCD. О - точка пересечения его диагоналей, точка К не принадлежит плоскости квадрата, причём АК=ВК=СК=DК. Как расположена прямая АО относительно сторон треугольника ВКD?

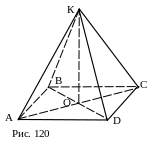
План решения.

1. АО  BD.

2. AO  OK.

3. Вывод.

№ 11. Доказать, что плоскость, проходящая через высоту и апофему правильной пирамиды, перпендикулярна стороне основания.

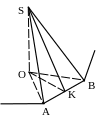План доказательства.

1. SK  AB.

2. OK  AB.

3. Вывод.

Рис. 121

№ 12. Прямая ВМ перпендикулярна к плоскости прямоугольника ABCD. Доказать, что прямая, по которой пересекаются плоскости ADМ и ВСМ, перпендикулярна к плоскости АВМ.

М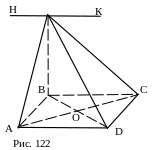

План доказательства.

1. Пусть НК – линия пересечения

плоскостей ADМ и ВСМ. НК|| AD.

2. AD^AВM.

3. НК^AВM.

№ 13 . Дано: ABCD – трапеция, АВ=СD,

О – центр окружности, описанной вокруг трапеции,

ОЕ^АВС. АЕ=10, ОЕ=8, ÐВАD=30°.

Найти: BD.

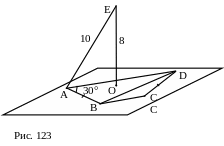План решения.

1. AEO – прямоугольный.

2. АО.

2. О – центр окружности,

описанной вокруг DABD.

3. BD (по теореме синусов).

№ 14. В основании пирамиды РАВСD лежит квадрат АВСD со стороной 6 см, а ребро РС перпендикулярно к основанию. Точка К лежит на боковом ребре АР и делит его в отношении 1: 2, считая от точки А. Найти расстояние от точки К до плоскости DPС.

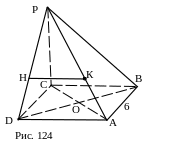План решения.

1.

2. HK || AD.

3. НК – искомое расстояние.

4. ~ ,

5. НК.

Ответ: 4.

№ 15. Через точки P и Q прямой PQ проведены прямые, перпендикулярные к плоскости a и пересекающие её в точках Р₁ и Q₁ соответственно. Найти Р₁Q₁, если PQ=15см, PP₁=21,5 см, QQ₁=33,5 см.

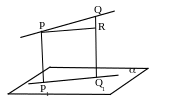План решения.

1. P₁PQQ₁ – трапеция.

2. Провести PR || P₁Q₁. P₁Q₁=PR.

3. QR.

4. PR.

Рис. 125

5. P₁Q₁. Ответ: 9 см

№16. Точка М принадлежит грани ADС тетраэдра ABCD, у которого AB=BD, AC=CD. Построить сечение тетраэдра плоскостью, проходящей через точку М и перпендикулярной ребру AD.

П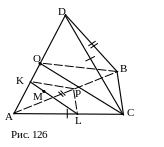 лан построения.

1. Точка О: АО=OD.

2. СО ^ АD.

3. KL: MÎ KL, KL||CO.

4. OB (OB^AD).

5. KP||OB.

6. LP.

7. LKP–искомое сечение. Доказать.

№ 17. Дан прямоугольный параллелепипед ABCDA₁В₁C₁D₁ и точка М, являющаяся внутренней точкой сечения АА₁С₁С. Построить сечение параллелепипеда плоскостью, проходящей через точку М и перпендикулярной: 1) прямой ВВ₁; 2) прямой ВС.

1) План построения.

1. F

   А₁

   L: MÎ FL, FL || AC.

2. FK ||AB. 3.KL.

4. LH || DC.

5. FH

6. FKLH – искомое сечение Доказать.

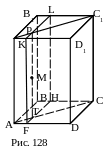2) План построения.

1. РТ: МÎ РТ, РТ || АА₁.

2. FH: Т FH, FH || AB.

3. FKLH – искомое сечение. Доказать.

№ 18. Пусть АВСDA₁B₁C₁D₁ - куб. Построить сечение этого куба плоскостью, проходящей через вершину А и перпендикулярной:

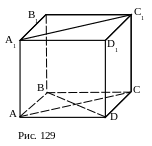
1) BD.

План построения.

1. АС.

2. АА₁С₁С – искомое сечение. Доказать.

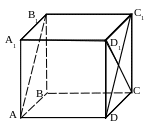2) CD₁.

План построения.

1. С₁D.

2. AB₁C₁D– искомое сечение. Доказать.

Рис. 130

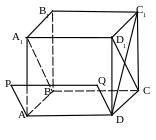
3) С₁D.

План построения.

1. BA₁ D₁C ^ C₁D. Доказать.

2. APQD || BA₁CD₁.

3. AD – искомое сечение.

Рис.131

№ 19. Пусть РАВС – правильный тетраэдр, точка Q – центр его основания, точка К – середина ребра РС. Постройте его сечение плоскостью, проходящей:

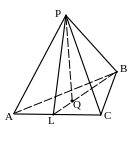1) через Q перпендикулярно АС.

План построения.

1. BQ

2. L – точка пересечения AC и BQ.

3. PLB – искомое сечение. Доказать.

Рис. 132

2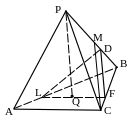 ) через Q перпендикулярно РВ.

План построения.

1. LF: LF || AC, Q Î LF.

2. М – середина РВ.

3. FD || CM.

4. LDF – искомое сечение. Доказать.

Рис. 133

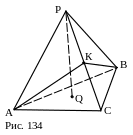
3) через К перпендикулярно РС.

План построения.

1. АК.

2. КВ.

3. АКВ – искомое сечение. Доказать.

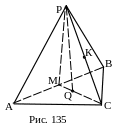
4) через К перпендикулярно АВ.

План построения.

1. CQ.

2. М – точка пересечения CQ и АВ.

3. МРС – искомое сечение. Доказать.

5) через Р перпендикулярно ВК.

План построения.

1. AO ^ CPM.

2. Прямая l : l || AO, PÎ l.

3. Плоскость a: PBÌ a и l Ì a.

4. РВ – искомое сечение. Доказать.