44,Линейные неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами.

Называется уравнение вида:

(1)

Где а1, а2, …, аn постоянные действительные числа.

Решение этого уравнения можно записать в виде:

Y= ,

А частное решение можно найти с помощью метода вариаций.

Если правая часть имеет специальный вид, то частное решение можно найти методом “подбора”. Общий вид правой части уравнения (1) при котором можно применять метод подбора следующий:

F(x)= ,

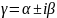
Где Pn и Qm многочлены.

Рассмотрим некоторые частные случаи:

1)F(x)=Pn(x), =0 если число совпадает с корнями характеристического ур-ния и S- число совпадений, то говорят что есть резонанс в степени S.

Если нет резонанса, то частное решение ищем в виде:

, где - многочлен n-ой степени с неопределёнными коэффициентами.

представляя данное решение в исходное уравнение.

, то частное решение ищем в виде :

f(x)=Pn(x) ,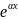

если нет резонанса:

если есть резонанс: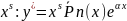

f(x) = Pn(x)cos +Qn(x)sin ,

Если нет резонанса, то: cos + , k=max[n,m];

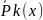( cos + ;

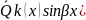Если правая часть представляет собой сумму выражений специального вида, то находим несколько частных решений и их складываем.

45.Системы дифференциальных уравнений.

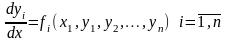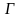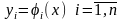Системы дифференциальных уравнений Система такого вида называется нормальной системой дифференциальных уравнений (СНДУ). Теорема. Если функции определены и непрерывны на открытом множестве , а соответствующие частные производные тоже непрерывны на , то тогда у системы будет существовать решение Системы линейных дифференциальных уравнений

Определение. Система Дифференциальных Уравнений называется линейной, если она линейна относительно всех неизвестных функций и их производных.

Теорема 1. Если определитель Вронского для линейной однородной системы с непрерывными на отрезке коэффициентами , равен нулю хотя бы в одной точке , то решение линейно зависимы на этом отрезке и, следовательно, определитель Вронского равен нулю на всем отрезке.Решение системы Дифференциальных Уравнений вида может быть представлено в виде , каждое из

которых удовлетворяет уравнению ,тогда .

46.Функции комплексной переменной. Предел и непрерывность функции комплексной переменной.

Если каждой точке z = х + iy некоторого множества Е поставленно в со­ответствие одно или несколько комплексных чисел w = и + iv, то говорят, что на множестве Е определена функция (однозначная или многозначная) комплексного переменного w = f(z).

Функцию f(z) можно рассматривать как пару функций и{х,у) и v{x,y).

и{х,у) = Re/O + iу), v(x,y) = Imf(z + iy).

Предел и непрерывность функции комплексной переменной:

Число А называется (

Функция f(z) называется неприрывной в точке z0 , если предел f(z) z стремится к z0 =f(z0) .

47.Производная функции комплексной переменной. Геометрический смысл модуля и аргумента производной.

Опр. Пусть в области D компл. переменной z задана функция f(z). Если для точки z_0ÎОD,  при DDz®®0 предел разностного отношения ,то этот предел называется производной функции f(z) по комплексной переменной z в точке z₀.

Теор. (Условие Коши-Римана)Если функция f(z) = u(x,y) + i v(x,y) диф-ма в точке z₀ = x₀ + i y₀, то в точке (x₀,y₀) $$ частные производные функций u(x,y) и v(x,y) по переменным x, y. Причем

,

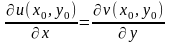Пусть f(z) аналитическая в точке z₀ и f ^‘(z₀) неравно нулю. Тогда коэффициенту дифформации в точке z₀ при отображении функции f(z) в плоскости z на плоскости w

При

При

Аргумент производной f ^‘(z₀) равен углу на который нужно повернуть касательную в т. z₀ к любой гладкой прямой плоскости z проходящею через т. z_0.

Что бы получить направление касательной к образу этой кривой по пл. при отображении .

48.Понятие аналитической функции, условия Коши-Римана. Связь аналитических и гармонических функций. Конформные преобразования.Опр. Если функция f(z) диф-ма во всех точках некоторой области J, а ее производная непрерывна в этой области, то функция f(z) называется аналитической в области J.

аналитичности функции f(z) = u(x,y) + i v(x,y) в области J необходимо и достаточно сущ-е непрер. частных производных функций u(x,y), v(x,y), связанных условиями Коши-Римана.

Теор. (Условие Коши-Римана)Если функция f(z) = u(x,y) + i v(x,y) диф-ма в точке z₀ = x₀ + i y₀, то в точке (x₀,y₀) $$ частные производные функций u(x,y) и v(x,y) по переменным x, y. Причем

, Пусть функция w = f (z) = u + iv регулярна в области D. Тогда она удовлетворяет условиям Даламбера –Эйлера : Дифференцируя первое из этих тождеств по х, а второе по y и складывая, получим: Дифференцируя же первое из этих тождеств по y, а второе по х и вычитая, будем иметь: Равенства и говорят о том, что функции u (x,y) и v (x,y), являюшиеся соответственно действительной и мнимой частями функции w = f (z), регулярной в некоторой области D, в той же области являются решениями дифференциального уравнения в частных производных: Дифференциальное уравнение называется уравнением Лапласа. Функция, являющаяся решением уравнения Лапласа, называется гармонической. Следовательно, действительная и мнимая части регулярной функции являются гармоническими функциями. Отображение, обладающее свойством постоянства коэффициента растяжения и консерватизма углов, называется Конформные преобразования., преобразования осуществляемое регулярной функцией, является конформным во всех точках, в которых производная этой функции отлична от нуля.