55. Вычеты аналитических функций. Основная теорема о вычетах.

В окрестности особой изолированной точки z=a аналитическая функция f(z) представляется сходящимся рядом Лорана f(z)=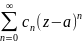 + . (1)

Среди коэффициентов ряда (1) особо выделяется коэффициент 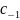. Он называется вычетом функции f(z) в точке z=a и обозначается 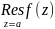. Итак, по определению = . Для коэффициентов ряда Лорана имеем = = ,

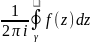Где - замкнутый контур, ориентированный положительно и окружающий точку z=a. В качестве контура можно взять окружность с центром в точке a, достаточно малым радиусом, не содержащую внутри особых точек функции f(z), кроме точки z=a. Теорема о вычетах: если f(z) является аналитической в области 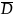, ограниченной контуром , за исключением конечного числа особых точек 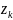(k=1, 2, 3,…,n), лежащих внутри области D, то = .

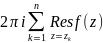56. Приложения вычетов к вычислению определённых интегралов.

И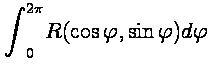 нтегралы виды  

     Для рациональной функции   указанные интегралы можно свести к контурным от функций комплексной переменной с помощью следующей замены переменных:

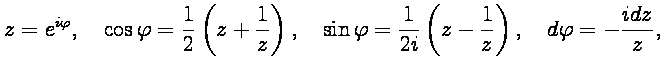
и так как   меняется в пределах от 0 до  , то точка   будет проходить окружность  . Тогда, после замены переменных в подынтегральном выражении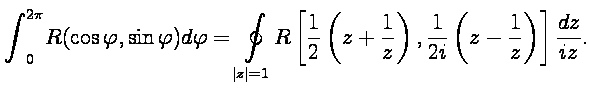

Обозначая

после применения теоремы о вычетах получим

где   - полюса функции  , принадлежащие области  .

Интегралы вида   

Вычисление интегралов такого типа основано на использовании следующей леммы: если функция   является аналитической в верхней комплексной полуплоскости   всюду, за исключением конечного числа особых точек, и выполнены условия 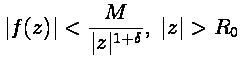 , тогда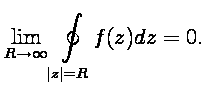

В этом случае для функции  , которая не имеет особых точек на оси  , справедлива формула вычисления несобственных интегралов:

где знак  + берется в случае, если суммирование выполняется для всех полюсов   в верхней полуплоскости   и - соответственно в нижней.

 Интегралы вида  

     Теорема о вычетах может быть использована для вычисления интегралов такого вида в случае выполнения условий следующей леммы (Жордана): пусть функция   - аналитическая в верхней полуплоскости, за исключением конечного числа изолированных особых точек, и равномерно относительно  стремится к нулю при  , тогда при  :

(78)

При таких условиях верна следующая формула вычисления интеграла:

(79)

Для случая   в формуле знак правой части меняется на противоположный, а суммирование производится по особым точкам функции   в нижней полуплоскости.

Интегралы вида  Методы вычисления интегралов, рассмотренные выше, даже при выполнении условий для функции   на бесконечности, тем не менее не могут быть здесь использованы, так как за счет присутствия множителя   полная подынтегральная функция может оказаться многозначной. В этом случае вспомогательный контур выбирается так, чтобы внутри него не содержалось точек ветвления функции  , а интегрирование выполнялось по какой-либо выбранной ветви  аналитической функции, чтобы обеспечить выполнение условий теоремы Коши. Если   не имеет особых точек, лежащих на положительной части действительной оси, то контур можно выбрать, при этом внутри не будет точек ветвления  . Применение теоремы о вычетах при выполнении таких условий приводит к следующему выражению для интеграла: