33.Тригонометрические ряды Фурье.
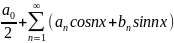,где
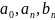-постоянные
коэффициенты.т.к. члены ряда имеют общий
периуд 2
,то
n
сумма ряда,если он содержит 2
переодическая функция.
Если ряд сходится
равномерно [-
то его коэффициенты определяются
формулами:
,
,
.
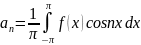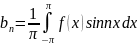Тригонометрический ряд коэффициенты которого задаются формулами , , .
Называется рядом Фурье.
Если функция f определена интегрирована на отрезке [- и раскладывается в тригонометрический ряд
Который равномерно сходится на [- то это разложение единственное.
34.Разложение в ряд Фурье четных и нечетных функций
Ряд Фурье для чётных функций:
,
,
.
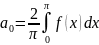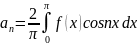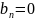Ряд Фурье для нечётных функций:
,
,
.
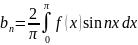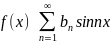
Если функция f(x)
определена на интервале (0;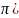
то продолжит её на промежуток (-
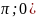чётным
или нечётным образом можно разложить
ее в ряд Фурье только по cos
или sin
Sin-нечётная cos-чётная
35.Ряд Фурье для функций, заданных на отрезке [-l;l].
,
,
.
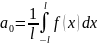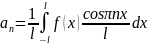Для чётной
Для нечётной
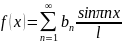
36. ИнтегралФурье.
Достаточные условия представимости функции в интеграл Фурье.
Для того, чтобы f(x) была представлена интегралом Фурье во всех точках непрерывности и правильных точках разрыва, достаточно:
1)
абсолютной интегрируемости на 
(т.е.
интеграл сходится)
2) на любом конечном отрезке [-L, L] функция была бы кусочно-гладкой
3) в точках разрыва функции, ее интеграл Фурье определяется полусуммой левого и правого пределов в этих точках, а в точках непрерывности к самой функции f(x)
Интегралом Фурье функции f(x) называется интеграл вида:
,
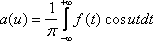
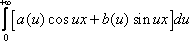
где
.
37. Косинус- и синус-преобразование Фурье.
Интегралы
.
называются
соответственно косинус- и
синус-преобразованиями Фурье. Из формул
(2) и (3) непосредственно следует, что если
к кусочно-гладкой функции 
применить
последовательно два раза косинус- (или
синус-) преобразование Фурье, то получим
исходную функцию 
.
В этом смысле косинус- (синус-) преобразование
Фурье является обратным самому себе.
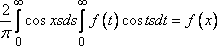. (2)
.
(3)
38.Дифференциальные уравнения. Основные определения
Дифференциальным уравнением называется уравнение относительно неизвестной функции и ее производных различных порядков.
Решение Дифференциального уравнения порядка n называется функция имеющая на некотором интервале производные порядка n включительно и удовлетворяющая этому уравнению. Порядком Дифференциального уравнения называется порядок старшей производной входящей в это уравнение .
Если искомая функция зависит от одной переменной то соответствующее
Дифференциальное уравнение называется ОБЫКНОВЕННЫМ.(ОДУ)
Если искомая функция зависит от нескольких переменных то соответствующее Дифференциальное уравнение называется уравнение с частными производными.
(ОДУ)
n-го
порядка можно записать:F(x,y,
,
… ,
Уравнение называется
разрешённым относительно старшей
производной если оно имеет вид:
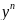=f(x,y,
,
… ,
.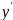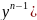