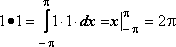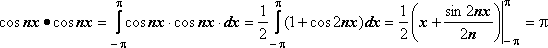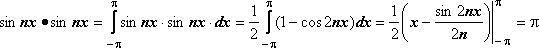28,Почленное интегрирование и дифференцирование функциональных рядов.

u1(x) + u2(x) +…+ un(x) +… , где un(x) = f (x,n), называется функциональным рядом.

Теорема о почленном интегрировании.

функция непрерывна на отрезке

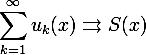на

Тогда

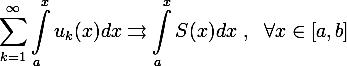
Теорема о почленном дифференцировании.

функция непрерывно дифференцируема на отрезке

сходится

равномерно сходится на отрезке .

Тогда 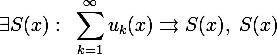— непрерывно дифференцируема 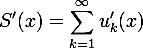на , на .

29.Степенной ряд и его область сходимости.

Степенной ряд – это ряд, в общий член которого входят целые положительные степени независимой переменной х.

записывают так:.

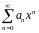
Область сходимости степенного ряда.

Теорема. Для всякого степенного ряда 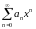существует такой интервал 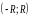(конечный или бесконечный), внутри которого ряд сходится абсолютно, а для всех таких, что 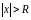, ряд расходится.

Определение. Интервал 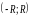называется интервалом сходимости, а число 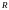радиусом сходимости ряда.

Теорема (Абеля). Пусть дан степенной ряд

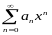,тогда:

1. Если ряд сходится в некоторой точке , то он сходится, и притом абсолютно, в любой точке такой, что .

2. Если ряд расходится в 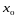, то он расходится во всех точках 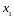таких, что .

Теорема. Пусть функция определена степенным рядом

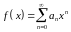, и пусть 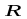- радиус сходимости этого ряда.

Тогда внутри интервала сходимости исходный степенной ряд можно почленно дифференцировать и интегрировать, то есть при всех 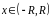будет верно

;

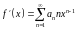Причем радиусы сходимости полученных рядов тоже будут равны .

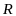30.Аналитические функции. Ряд Тейлора.

Аналити́ческая функция — функция, которая совпадает со своим рядом Тейлора в окрестности любой точки области определения.

Однозначная функция f называется аналитической в точке Zo , если сужение функции на некоторую окрестность является аналитической функцией. Если функция аналитична в точке Zo , то она аналитическая в каждой точке некоторой окрестности точки Zo .

Ряд Тейлора.

формула Тейлора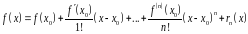 Определение. Рядом Тейлора для функции 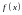с центром в точке называется ряд .

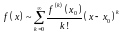Теорема. Если функция 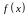в окрестности 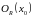имеет производные всех порядков, и все эти производные в данной окрестности ограничены в совокупности, то есть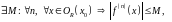

то во всем промежутке имеет место разложение .

.

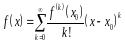31.Разложение в ряды Маклорена основных элементарных функций

1. Разложение функции f(x)=ex в ряд Маклорена.

f(x)=f′(x)=f″(x)=…=f(n)(x)=…=ex

2. Разложение функции f(x)=sinx в ряд Маклорена.

f′(x)=cosx=sin(x+ )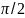

3.

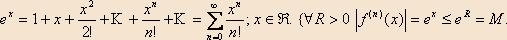
4.

5.

6.

7.

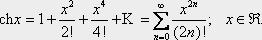
8.

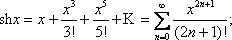
32.Тригонометрическая система функций.

Тригонометрической системой называется система

1, cos x , sin x ,…, cos 2x, sin 2x,…,cos nx, sin nx,…

Тригонометрическая система периодическая с периудом 2 .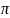

Интеграл по отрезку [-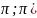 от произведения двух различных функций системы равен 0.

1)

2)

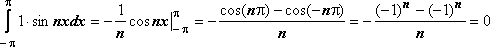
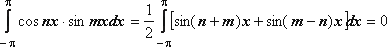
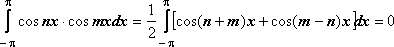
5.

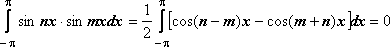
Интеграл по отрезку [- от квадрата любой функции системы отличен от 0.