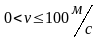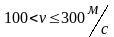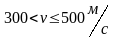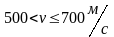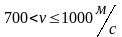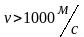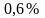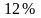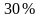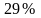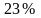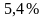- •51. Статистический и термодинамический методы исследования вещества.
- •52. Основные положения молскулярно-кинетичсской теории.
- •53. Максвелловский закон распределения молекул газа по их скоростям.
- •54. Больцмановский закон распосделсния молекул газа по их энергиям.
- •55. Закон равномерного распределения энергии по степеням свободы молекул газа.
- •56. Молекулярно-кинстическое толкование абсолютной температуры
- •57. Первое начало термодинамики.
- •58. Адиабатический процесс.
- •59. Политропические процессы
- •60. Второе начало термодинамики.
- •61. Изопроцессы. Запишите уравнения состояния идеального газа для этих процессов и начертите их графики в координатах р и V, р и t, t и V.
- •62. Дайте определение полной, молярной и удельной тсплоемкостей газа.
- •63Дайте определение равновесного и неравновесного состояния системы.
- •64. Дайте определение обратимого и необратимого процесса.
- •65. Дайте определение кругового процесса (цикла). Объясните принцип действия тепловых машин.
- •66. Начертите цикл Карно в координатах р и V
- •67. Дайте определение энтропии. Чему равно изменение энтропии для обратимых и необратимых процессов.
- •Энтропия и второе начало термодинамики
- •73. Приведите барометрическую формулу. Для чего она служит?
- •74. Получите формулу для средней длины свободного пробега молекул газа.
- •75. Какое явление переноса в идеальном газе описывается выражением
- •78. Получите выражения для молярных теплоемкостей всех изопроцессов в идеальном газе. 79Получите соотношение Манера
- •Соотношение Майера
- •Соотношение Майера
- •94. Начертите изотерму Ван-дер-Ваальса и сравните ее с экспериментальной изотермой реального газа.
- •95. Дайте определение критического состояния газа. Получите выражения для параметров критического состояния газа.
- •96. Получите формулу для внутренней энергия реального газа.
- •97. В чем заключается эффект Джоуля-Томсона?
- •98. Получите уравнение Клапейрона-Клаузиуса для фазового превращения реального газа.
- •99. Нарисуйте диаграмму равновесных давлений и температур для двухфазной системы "жидкость - пар".
- •100Нарисуйте обобщенную диаграмму состояний для трехфазной системы "твердое тело - жидкость - газ". Дайте определение тройной точки.
- •Фазовые превращения реального газа
- •Уравнение Клапейрона-Клаузиуса и фазовая диаграмма для превращения жг
- •Уравнение Клайперона-Клаузиуса и Рис. 6 фазовая диаграмма для превращения тж
- •Уравнение Клайперона-Клаузиуса и фазовая диаграмма для превращения тг. Тройная точка. Диаграмма состояния.
51. Статистический и термодинамический методы исследования вещества.
Существует два метода изучения свойств вещества: молекулярно-кинетический и термодинамический.
Молекулярно-кинетическая теория истолковывает свойства тел, которые непосредственно наблюдаются на опыте (давление, температуру и т.п.), как суммарный результат действия молекул. При этом она пользуется статистическим методом, интересуясь не движением отдельных молекул, а лишь средними величинами, которые характеризуют движение огромной совокупности частиц. Отсюда другое её название – статистическая физика.
Термодинамика изучает макроскопические свойства тел, не интересуясь их микроскопической картиной. В основе термодинамики лежит несколько фундаментальных законов (называемых началами термодинамики), установленных на основании обобщения большой совокупности опытных фактов. Термодинамика и молекулярно-кинетическая теория взаимно дополняют друг друга, образуя по существу единое целое.
52. Основные положения молскулярно-кинетичсской теории.
Все вещества состоят из мельчайших частиц - атомов и молекул.
Молекулы и атомы любого вещества находятся в непрерывном хаотическом движении, которое называется тепловым движением. При нагревании вещества интенсивность движения частиц увеличивается.
Молекулы вещества взаимодействуют между собой с силами притяжения Fпр и отталкивания Fот .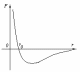
r = r0 , Fот = Fпр ,
r < r0 , Fот > Fпр ,
r > r0 , Fот < Fпр ,
r , F 0.
Характер движения молекул зависит от агрегатного состояния вещества.
Движение
молекул газов сводится к хаотическому
поступательному движению.Скорость
молекул газов зависит от температуры.Масса
молекулы:Молекулярная
масса вещества
– масса молекулы вещества, выраженная
в а.е.м.Атомная
единица массы (а.е.м.)
– единица массы, равная 1/12 массы атома
С12.Моль
– количество вещества, в котором
содержится число молекул, равное числу
атомов в 0,012 кг изотопа углерода С12.Число
частиц, содержащихся в моле вещества,
называется числом
Авогадро:NA
=
6,023
1023
моль-1Молярная
масса М
– масса моля вещества.Зная число
Авогадро, можно найти значение а.е.м.0,012
= NA
12
1 а.е.м.,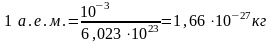 .Размеры
молекулы:Линейные
размеры молекул воды приблизительно
равны 3
10-10
м.
.Размеры
молекулы:Линейные
размеры молекул воды приблизительно
равны 3
10-10
м.
53. Максвелловский закон распределения молекул газа по их скоростям.
Возьмем идеальный газ. В результате столкновений молекул газа, их скорости все время изменяются, но в газе создается некоторое стационарное распределение молекул по их скоростям .
Пусть температура газа T = 300K.
Интервал скоростей |
Доля молекул, имеющих скорости в заданном интервале |
|
|
Максвелл в 1860 г. получил формулу, которая описывает распределение молекул по скоростям:
Максвелловское
распределение молекул по их скоростям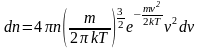 -
-
где n – число молекул в единице объема,
dn – число молекул в единице объема, имеющих скорость в интервале от v до v + dv,
m – масса молекулы,k – постоянная Больцмана,

Построим
кривые Максвелла для двух температур
( ).
).
Физический
смысл кривой Максвелла:
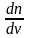 - число молекул, имеющих скорости в
единичном интервале скоростей. Возьмем
узкую полоску, которую можно считать
прямоугольной. Ее площадь равна :
- число молекул, имеющих скорости в
единичном интервале скоростей. Возьмем
узкую полоску, которую можно считать
прямоугольной. Ее площадь равна :
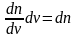 .
.
Тогда площадь под всей кривой Максвелла равна n.
Для того, чтобы придать вероятностный характер распределению Максвелла, введем новую функцию :
 -
функция
распределения Максвелла молекул по их
скоростям.
-
функция
распределения Максвелла молекул по их
скоростям.
График
этой функции имеет аналогичный вид, но
теперь площадь под кривой
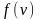 равна 1.
равна 1.
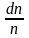 -
имеет смысл вероятности того, что
молекула имеет скорость в интервале от
-
имеет смысл вероятности того, что
молекула имеет скорость в интервале от
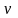 до
до
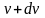 .
Согласно определению функции
имеем
.
Согласно определению функции
имеем
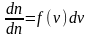 ,
откуда видно, что
,
откуда видно, что
- плотность вероятности того, что молекула имеет скорость в интервале от до .
Это очень важная величина в теории вероятности, позволяющая вычислять среднее значение любой физической величины, являющейся функцией скорости .
От
распределения молекул по скоростям
можно перейти к распределению молекул
по их кинетической энергии
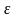 .
Для этого надо распределении молекул
по скоростям выразить
и
.
Для этого надо распределении молекул
по скоростям выразить
и
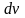 через
и
через
и
 .
.
 ,
,
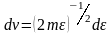 .
.
Производя вычисления, получим
Максвелловское
расрпеделение молекул по их кинетическим
энергиям.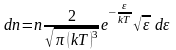 -
-

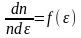 -
функция
распределения Максвелла молекул по их
энергиям.
-
функция
распределения Максвелла молекул по их
энергиям.