
- •Э лектрический заряд. З-н сохранения эл. Заряда. З-н Кулона.
- •Напряженность эл-кого поля. Принцип суперпозиции полей.
- •Потенциал эл. Поля и его связь с напряженностью.
- •Циркуляция и ротор векторного поля.
- •Энергия эл. Поля.
- •Электрический ток. Условия сущ-я эл. Тока. Сила тока.
- •Электродвижущая сила.
- •Мощность тока.
- •Магнитное поле. Индукция магнитного поля.
- •Дифф-ое ур-ние электромагн. Волны. (no comm)
- •Классич. Т-я электропроводиимости. Природа носителей тока в металлах.
- •Класич. Т-я электропров. Друде.
- •Эффект Холла.
Э лектрический заряд. З-н сохранения эл. Заряда. З-н Кулона.
Все тела способны электризоваться, т.е. приобретать заряд, что проявляется во взаимодействии наэлектризованных тел друг с другом. Обладает св-м дискретности, т.е. кратен элементарному заряду. Заряд инвариантен, т.е. величина заряда не зависит от выбора сис-мы коорд.
З-н сохранения: В изолированной сис-ме заряд постоянен.
З-н Кулона:
![]()
Напряженность эл-кого поля. Принцип суперпозиции полей.
Эл. поле – вид материи, посредством кот. взаимодействуют эл. заряды. Характеризуется в каждой точке вектором напряж. Е‾ и потенциалом φ.
Напряженность – отношение силы F‾, с которой поле в данной точке действует на заряд, к величине этого заряда: E‾ = F‾ / q0
![]()
Напряженность эл. поля нескольких точечных зарядов равна векторной сумме напряж. полей, которые создавал бы каждый из этих зарядов в отдельности: E‾=ΣEi‾
Потенциал эл. Поля и его связь с напряженностью.
Потенциал – отношение потенц. энергии, которую приобретает заряд в поле, к величине этого заряда. [Вольт] – потенциал точки поля, в кот. заряд в 1 К обладает потенциальной энергией 1 Дж. Потенциал поля точечного заряда:
![]()
Сила F связана с потенциальной энергией соотношением:
F‾=–gradWp. (*)
Для заряженной частицы, находящейся в электростатическом поле, F‾=qЕ‾, Wp =q φ. Подставив в (*) и преобразовав получим конечную формулу => E‾=–gradφ
Работа перемещения заряда в эл. поле.
dA = F•dl•cosα = Fdr
т.к. F‾=
q0E,
а
то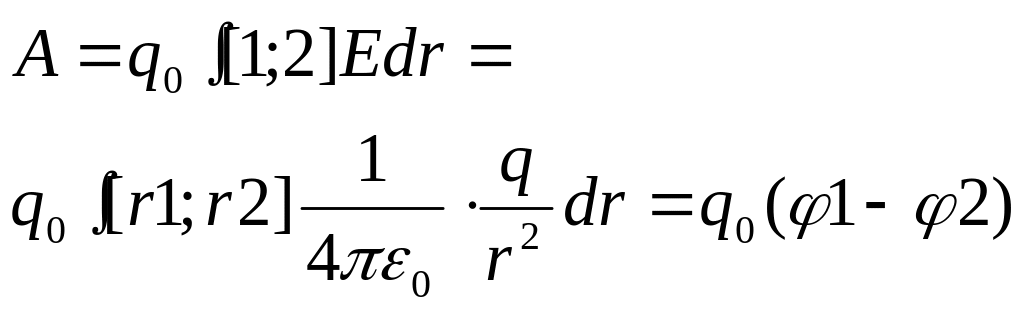
Теорема о циркуляции электростатич. поля . Потенц. хар-р электрост. поля.
Циркуляция вектора напряженности электрост. поля по замкнутому контуру равна нулю.
![]() Док-во:
Док-во:
![]() =>
при φ1=φ2,
=>
при φ1=φ2,
![]()
Следствия: 1) Работа сил поля не зависит от траектории, по кот. перемещается заряд. 2) Вектор Е всегда перпендикулярен пов-ти равного потенциала.
Поток вектора напряженности. Т-ма Гаусса для электрост. поля в вакууме.
Поток вект. Е‾
через пов-ть dS
наз. физ. величина, равная
![]()
Т. Гаусса: Поток вектора напряженности через замкнутую пов-ть равен алгебр. сумме зарядов, заключенных внутри этой пов-ти, деленной на ε0 :
![]()
Применение т. Гаусса к вычислению полей внутри и во вне заряженной сферы.
![]() ,
где Er
– пр-ция в-ра E‾
на радиус-вуктор r‾
проведенный из О в рассм. точку поля.
=>Er
= q
/ 4πε0r2
((внутри сферы q
= 0 => Er
= 0 ))
,
где Er
– пр-ция в-ра E‾
на радиус-вуктор r‾
проведенный из О в рассм. точку поля.
=>Er
= q
/ 4πε0r2
((внутри сферы q
= 0 => Er
= 0 ))
Применение т. Гаусса к вычислению поля бесконечной заряженной нити. (no comments):)
Применение т. Гаусса к вычислению поля бесконечной заряженной плоскости.
Рассм. безгр. пл-сть, заряженную полож. зарядом с плостностью σ = dq / dS. Линии напряж. перпендик. пл-ти. В качестве замкнутой пов-ти выберем прямой цилиндр. Полный поток в-ра Е‾ сквозь цилиндр равен сумме потоков через его основания: Ф = 2ЕS.
Т.к. полный заряд, заключенный внутри цилиндра, равен σS, то на основании т. Гаусса: 2ES= σS / ε0. Откуда E = σ / 2 ε0
Понятие диполь.
Сис-ма из двух близко расположенных зарядов, равных по величене и противопол. по знаку. Век-р l‾, проведенный от отрицательного заряда к положительному, наз. плечем диполя. Век-р p‾ = ql‾ наз. дипольным моментом. Молекула неполярного диэлектрика не имеет собственный дип. момент. М-ула полярного диэл. обладает дип. моментом.
Электрический диполь во внешнем эл. поле. Потенц. энергия диполя.
Под действием внешнего эл. поля происходит ориентация диполей по направлению поля, т.к. действует пара сил, стремящаяся повернуть его по направлению Е.
Диполь, находящийся в эл. поле, обладает потенциальной энергией Wп = –pEcosα
Идеальный проводник в электростатич. поле. Пов-ная плотность заряда. Граничные усл-я на границе «проводник-вакуум». (no comments):)
Электроемкость.
Эл. емкость – отношение заряда q проводника к его потенциалу φ. С = q / φ. Т.е. емкость – заряд, кот. нужно сообщить проводнику, что бы изменить его потенциал на единицу.
Зависит от геометрии проводника, а также диэлектрических свойств среды.
Конденсаторы. Энергия конденсатора. Электроемкость плоского, сферич., цилиндр. конденсаторов.
Электрический конденсатор – устройство, предназначенное для накапливания электрических зарядов. Конденсатор состоит из двух проводников (обкладки), имеющих такую форму, чтобы эл. поле было сосредоточено между обкладками. Обкладки заряжаются электрическими зарядами противоположных знаков.
Емкость плоского конденсатора рассчитывается по формуле: C=εε0S /d
-цилиндрического конденсатора С = 2πεε0h / ln(R2-R1) где h- длина конденсатора, R1 и R2 - радиусы внутренней и внешней обкладок.
-сферического конденсатора равна: С=4πεε0R1R2 /(R2-R1) где R1 и R2 — радиусы внутренней и внешней обкладок.
Заряженный конденсатор обладает запасом энергии, которая выделяется при разрядке конденсатора. Носителем энергии является электрическое поле, сосредоточенное между обкладками конденсатора.
![]()
Электрическое поле в диэлектриках.
В результате поляризации на пов-ти диэлектрика возникают нескомпенсированные связанные заряды, которые создают поле напряженностью Е’, направленное противоположно внешн. полю E0. Поле в диэлектрике является суперпозицией поля E0, созданного свободными зарядами, и поля Е’.
Е = E0 – E’.
Поляризация диэлектриков.
При внесении полярного диэл. в эл. поле происходит ориентация диполей по направлению поля, т.к. на каждый диполь действует пара сил, стремящаяся повернуть его по направлению Е. (Ориентационная поляризация)
В неполярной молекуле под действием сил поля полож. и отриц. заряды смещаются в противополож. стороны, молекула приобретает дипольный момент. (Электронная поляризация)
Объемные и поверх-ные связанные заряды.
В рез-те поляризации у диэлектрика появляется пов-ная плотность связанных зарядов. σ’= Pcosα, где P – поляризованность. ((q = Sσ’))
Объемная плотность ρ’ = – divP, P‾ – в-р поляризованности. ((q = Vρ’))
Электрическое смещение. Т. Гаусса для эл. смещения.
Чтобы вычислить напряж. поля в диэл., нужно знать плотность связанных зарядов, что в ряде случаев затруднительно. Для упрощения вводят вспомогательную величину, не зависящую от св-в среды. D‾ = ε0εE‾=(1+x) ε0E‾= ε0E‾ + P‾.. ((divD‾=ρ))
т. Гаусса: Поток в-ра D‾ через замкнутую пов-ть равен алгебраической сумме заключенных внутри сторонних зарядов.
![]()
Условия на границе раздела двух диэлектриков.
D‾ и E‾ на границе разделов диэлектриков испытывают преломления в соответствии с условиями:
1)Eτ1= Eτ2 2)Dτ1/ Dτ2 = ε1/ε2 3)Dn2=Dn1 4) En1 / En2 = ε2/ε1
Сегнетоэлектрики и их св-ва.
Наз. полярные диэлектрики, которые определенном температурном интервале самопроизвольно поляризованы. Св-ва: 1) ε может достигать неск. тысяч и зависит от Е внешнего эл. поля. 2) температурная зависимость ε имеет один или неск. реско выраженных макс-ов. 3) сущ. темп-ра, выше которой СЭ утрачивает свои св-ва (точка Кюри), или температурный интервал. 4) зависимость поляризованности P‾ от E‾ имеет вид петли гистерезиса.
