
- •Оптическая длина пути световой волны
- •Оптическая разность хода двух световых волн
- •Условие усиления света (максимумов) при интерференции
- •Разрешающая способность дифракционной решетки
- •1. радиуса n -й стационарной орбиты электрона
- •Из данной формулы может быть получена формула Бальмера для длины волны излучения атома водорода, полученная им эмпирически.
- •Закон радиоактивного распада можно также записать в форме
- •Активность А радиоактивного изотопа
1
МИНИМАЛЬНЫЙ СПИСОК ЭКЗАМЕНАЦИОННЫХ ВОПРОСОВ ПО ФИЗИКЕ (РАЗДЕЛ “ОПТИКА, ЭЛЕМЕНТЫ АТОМНОЙ И ЯДЕРНОЙФИЗИКИ”) ДЛЯ ЗАОЧНИКОВ
1.Световое излучение и его характеристики
Свет представляет собой материальный объект, обладающий двойственной природой (корпускулярно-волновым дуализмом). В одних явлениях свет ведёт себя как электромагнитная волна (процесс колебаний электрических и магнитных полей распространяющийся в пространстве), в других – как поток особых частиц - фотонов или квантов света.
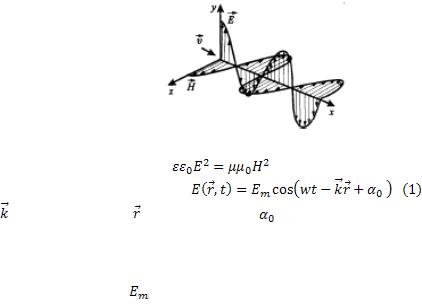
В электромагнитной волне вектора напряжённости электрического поля E, магнитного поля H и скорость распространения волны V взаимно перпендикулярны и образуют правовинтовую систему.
Вектора E и H колеблются в одной фазе. Для волны выполняется условие:
Уравнение световой волны имеет |
, где ω– циклическая |
частота, - волновое число, - радиус-вектор, |
- начальная фаза. |
При взаимодействии световой волны с веществом наибольшую роль играет электрическая составляющая волны (магнитная составляющая в немагнитных средах влияет слабее), поэтому вектор E (напряжённость электрического поля волны) называют световым вектором и его амплитуду обозначают А.
Характеристикой переноса энергии световой волны является интенсивность I – это количество энергии переносимое за единицу времени световой волной через единицу площади, перпендикулярной направлению распространения волны. Линию, по которой распространяется энергия волны, называется лучом.
2. Отражение и преломление плоской волны на границе 2-х диэлектриков. Законы отражения и преломления света.
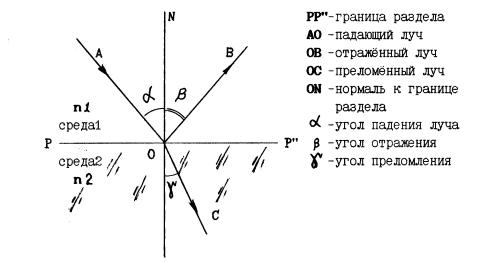
Закон отражения света: луч падающий, луч отражённый и нормаль к границе раздела
сред в точке падения лежат в одной плоскости. Угол падения равен углу отражения (α=β). Причём падающий и отражённый лучи лежат по разные стороны нормали.
Закон преломления света: луч падающий, луч преломлённый и нормаль к границе раздела сред в точке падения лежат в одной плоскости. Отношение синуса угла падения к синусу угла преломления – величина постоянная для данных двух сред и называется относительным показателем преломления или показателем преломления второй среды относительно первой.
sin α / sin γ = n21 = n2 / n1
2
где n21 - относительный показатель преломления второй среды относительно первой,
n1,n2 - абсолютные показатели преломления первой и второй сред (т.е. показатели преломления сред по отношению к вакууму).
Среду, у которой показатель преломления больше, называют оптически более плотной. При падении луча из оптически менее плотной в оптически более плотную среду (n2>n1)
угол падения больше угла преломления α>γ (как на рис.).
При падении луча из оптически более плотной в оптически менее плотную среду (n1> n2) угол падения меньше угла преломления α<γ. При некотором угле падения
преломленный луч будет скользящим к поверхности (γ=90о). Для углов больше этого угла падающий луч полностью отражается от поверхности (явление полного внутреннего отражения).
Относительный показатель n21 |
и абсолютные показатели преломления сред n1 и n2 можно |
|||||||||
также выразить через скорости света в средах |
||||||||||
n21 = |
v1 |
, |
n1 = |
c |
, n2 |
= |
c |
, где с- скорость света в вакууме. |
||
|
|
|
||||||||
|
v |
2 |
|
|
v |
|
v |
2 |
|
|
|
|
|
1 |
|
|
|
|
|||
3. Когерентность. Интерференция световых волн. Интерференционная картина от двух источников.
Когерентность – согласованное проникание двух или более колебательных процессов. Когерентные волны при сложении создают интерференционную картину. Интерференция – процесс сложения когерентных волн, заключающийся в перераспределении энергии световой волны в пространстве, которое наблюдается в виде тёмных и светлых полос.
Причина отсутствия наблюдения интерференции в жизни – это некогерентность естественных источников света. Излучение таких источников образуется совокупностью излучений отдельных атомов, каждый из которых в течение ~10-8с испускает «обрывок» гармонической волны, который называется цугом.
Когерентные волны от реальных источников можно получить, разделяя волну одного источника на два и более, затем, давая возможность им пройти разные оптические пути, свести их в одной точке на экране. Пример – опыт Юнга.
3
Оптическая длина пути световой волны
L = n l ,
где l — геометрическая длина пути световой волны в среде с показателем преломления п.
Оптическая разность хода двух световых волн
∆ = L1 −L2 .
Условие усиления света (максимумов) при интерференции
∆ = ±k λ , где k=0, 1, 2, 3 , λ — длина световой волны.
Условие ослабления света (минимумов)
∆ = ±(2k +1)λ2 , где k=0, 1, 2, 3 ……
Расстояние между двумя интерференционными полосами, создаваемыми двумя когерентными источниками света на экране, расположенном параллельно двум когерентным источникам света
∆y = dL λ ,
где L — расстояние от источников света до экрана, d — расстояние между источниками
(d<<L).
4. Интерференция в тонких пленках. Полосы равной толщины, равного наклона, кольца Ньютона.
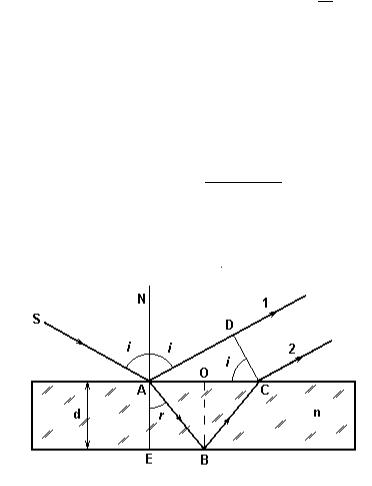
Оптическая разность хода световых волн, возникающая при отражении монохроматического света от тонкой пленки
∆ = 2d 
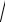 n2 −sin2 i ± λ2 или ∆ = 2dncosr ± λ2
n2 −sin2 i ± λ2 или ∆ = 2dncosr ± λ2
где d — толщина пленки; n — показатель преломления пленки; i — угол падения; r — угол преломления света в пленке.
Если зафиксировать угол падения i и взять плёнку переменной толщины, то для определённых участков с толщиной d реализуются интерференционные полосы равной
4
толщины. Эти полосы можно получить, если направить параллельный пучок света на пластинку с разной толщиной в разных местах.
Если на плоскопараллельную пластинку (d = const) направить расходящийся пучок лучей (т.е. пучок, который обеспечит различные углы падения i), то при наложении лучей, падающих под определенными одинаковыми углами, будут наблюдаться интерференционные полосы, которые называют полосами равного наклона
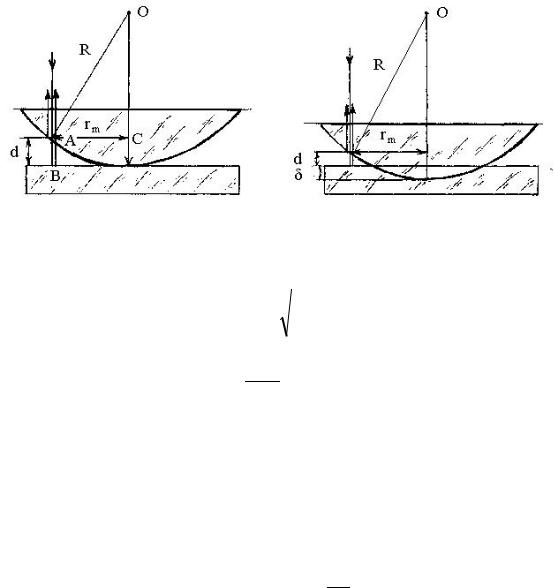
Классический пример полос равной толщины – кольца Ньютона. Они образуются, если на плосковыпуклую линзу, лежащую на стеклянной пластине, направить монохроматический пучок света. Кольца Ньютона представляют собой интерференционные полосы от областей с равной толщиной воздушного промежутка между линзой и пластинкой.
Радиус светлых колец Ньютона в отраженном свете
r = |
|
(2k −1)Rλ |
|
, |
|
||||
k |
2 |
|||
|
|
|
|
|
где k=1, 2, 3 …… — номер кольца; R — радиус кривизны. Радиус темных колец Ньютона в отраженном свете
rk = 
 kRλ , где k=0, 1, 2, 3 …….
kRλ , где k=0, 1, 2, 3 …….
5. Просветление оптики
Просветление оптики – состоит в том, что на поверхность стеклянной детали наносится тонкая прозрачная плёнка, которая за счёт интерференции устраняет отражение падающего света, повышая, таким образом, светосилу прибора. Показатель преломления
просветляющей пленки n должен быть меньше показателя преломления стеклянной детали
nоб. Толщина этой просветляющей пленки находится из условия ослабления света при интерференции по формуле
dmin = 4λn
5
6. Дифракция света. Принцип Гюйгенса-Френеля. Дифракция Френеля. Метод зон Френеля. Векторная диаграмма зон Френеля. Дифракция Френеля на простейших преградах (круглом отверстии).
Дифракция света это совокупность явлений, заключающихся в перераспределении светового потока при прохождении световой волны в средах с резкими неоднородностями. В узком смысле дифракция – это огибание волнами препятствий. Дифракция света приводит к нарушению законов геометрической оптики, в частности – законов прямолинейного распространения света.
Между дифракцией и интерференцией нет принципиальной разницы, т.к. оба явления приводят к перераспределению энергии световой волны в пространстве.
Различают дифракцию Фраунгофера и дифракцию Френеля.
Дифракция Фраунгофера – дифракция в параллельных лучах. Наблюдается когда экран или точка наблюдения расположены далеко от препятствия.
Дифракция Френеля – это дифракция в сходящихся лучах. Наблюдается на близком расстоянии от препятствия.
Качественно явление дифракции объясняется принципом Гюйгенса: каждая точка фронта волны становит источником вторичных сферических волн, а новый фронт волны представляет собой огибающую этих вторичных волн.
Френель дополнил принцип Гюйгенса идеей о когерентности и интерференция этих вторичных волн, что дало возможность рассчитывать интенсивность волны для разных направлений.
Принцип Гюйгенса-Френеля: каждая точка фронта волны становится источником когерентных вторичных сферических волн, а новый фронт волны образуется в результате интерференции этих волн.
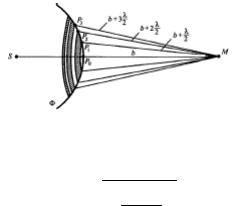
Френель предложил симметричные волновые поверхности разбивать на особые зоны, расстояния от границ которых до точки наблюдения различаются на λ/2. Соседние зоны действуют в противофазе, т.е. амплитуды, создаваемые соседними зонами в точке наблюдения, вычитаются. Для нахождения амплитуды световой волны в методе зон Френеля используется алгебраическое сложение амплитуд, создаваемых в этой точке зонами Френеля.
.
Радиус внешней границы m-ой кольцевой зоны Френеля для сферической волновой поверхности
rm = 
 m aab+b λ ,
m aab+b λ ,
где a –расстояние от источника света до волновой поверхности, b – расстояние от волновой поверхности до точки наблюдения.
Векторная диаграмма зон Френеля представляет собой спираль. Использование векторной диаграммы упрощает нахождение амплитуды результирующего колебания

6
напряженности электрического поля волны A (и, соответственно, интенсивности I~A2) в центре дифракционной картины при дифракции световой волны на различных препятствиях. Результирующий вектор А от всех зон Френеля представляет собой вектор, соединяющих начало и конец спирали.
При дифракции Френеля на круглом отверстии в центре дифракционной картины будет наблюдаться тёмное пятно (минимум интенсивности), если в отверстии укладывается чётное число зон Френеля. Максимум (светлое пятно) наблюдается, если в отверстии укладывается нечётное число зон.
7.Дифракция Фраунгофера на щели.
Угол ϕ отклонения лучей (угол дифракции), соответствующий максимуму (светлая полоса) при дифракции на одной узкой щели, определяется из условия
bsinϕ = (2k +1) λ2 , где k= 1, 2, 3,...,
где b — ширина щели; k — порядковый номер максимума.
Угол ϕ отклонения лучей, соответствующий минимуму (темная полоса) при дифракции на узкой щели, определяется из условия
bsinϕ = k λ , где k= 1, 2, 3,...,
где b — ширина щели; k — порядковый номер максимума.
Зависимость интенсивности I от угла дифракции ϕ для щели имеет вид
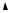 Iϕ
Iϕ
I0
|
m=2 m=1 |
|
|
m=1 |
m=2 |
-sinφ |
-2λ/b -λ/b |
0 |
+λ/b |
+2λ/b |
+3λ/b sinφ |
7
8.Дифракция Фраунгофера на дифракционной решетке.
Одномерная дифракционная решётка представляет собой систему из периодически расположенных прозрачных и непрозрачных для света областей.
Прозрачная область – это щели шириной b. Непрозрачные области – щели с шириной a. Величина a+b=d называется периодом (постоянной) дифракционной решётки. Дифракционная решётка разбивает световую волну, падающую на неё на N когерентных волн (N – общее количество целей в решётке). Дифракционная картина является результатом наложения дифракционных картин от всех отдельных щелей.
Внаправлениях, в которых волны от щелей усиливают друг друга, наблюдаются главные максимумы.
Внаправлениях, в которых ни одна из щелей не посылает свет (для щелей наблюдаются минимумы) образуются абсолютные минимумы.
Внаправлениях, где волны от соседних щелей «гасят» друг друга, наблюдается
вторичные минимумы.
Между вторичными минимумами наблюдаются слабые вторичные максимумы.
Зависимость интенсивности I от угла дифракции ϕ для дифракционной решетки имеет вид
m=1 m=1
|
|
m=2 |
m=2 |
|
|
m=8 m=7 |
m=5 |
m=4 |
m=4 |
m=5 |
m=7 m=8 |
|
|
|
− 7λ |
|
− 5λ − 4λ − |
|
O |
2λ |
4λ 5λ |
|
7λ |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
3λ |
d |
2λ |
d |
d |
λ |
d |
d |
|
d d λ |
d |
d |
2λ |
d |
3λ |
|
|
|
|||||||||||||
b |
− |
b |
|
|
− b |
|
|
|
b |
|
|
b |
|
b |
|
Угол ϕ отклонения лучей, соответствующий главному максимуму (светлая полоса) при дифракции света на дифракционной решетке, определяется из условия
d sinϕ = ±mλ, где m=0, 1, 2, 3,...,
где d — период дифракционной решетки, m — порядковый номер максимума (порядок спектра).
9.Дифракция на пространственных структурах. Формула Вульфа - Брэгга.
Формула Вульфа — Брэгга описывает дифракцию рентгеновских лучей на
кристаллах с периодическим расположением атомов в трех измерениях
