11.Нормальные подгруппы и факторгруппы.

Пусть G = (S;*) – группа, а H = (T;*), T S, - ее подгруппа. Подгруппа H называется нормальной подгруппой группы G, если для каждого элемента a S его левые и правые смежные классы совпадают, т.е. если aH = Ha Заметим, что каждая подгруппа абелевой группы нормальна. Если подгруппа H нормальна в группе G, то ее левостороннее и правостороннее разложения группы G по группе H совпадают. Пусть G = (S;*) – группа, и N = (T;*) – ее нормальная подгруппа. Рассмотрим разложение группы G по нормальной подгруппе N. Введем операцию умножения смежных классов: если элементы a, b S, то (aN)(bN) = (ab)N. Оно определяет структуру группы на множестве классов смежности, а полученная группа G называется факторгруппой N по .

12.Гомоморфизм групп, его виды, примеры. Ядро гомоморфизма, его свойства.

Гомоморфизмы. Пусть G₁и G₂— группы. Нам хотелось бы исследовать функции из G₁в G₂, но не все, а лишь те, которые сохраняют групповую операцию. Определение - Гомоморфизмом групп (или просто гомоморфизмом) из группы G₁в группу G₁называется функция f: G₁ → G₂ сохраняющая групповую операцию, т. е. для любых x, у G выполнено свойство ƒ(x · y) = ƒ(x) · ƒf(y).

Ядром гомоморфизма ƒ называется множество Образом гомоморфизма ƒ называется множество

Лемма Кеrƒ — нормальная подгруппа в .

13.Подгруппа, порожденная данным множеством. Нормальная подгруппа, порожденная данным множеством.

…Подгруппа ― подмножество H группы G, само являющееся группой относительно операции, определяющей G .Подмножество H группы G является её подгруппой тогда и только тогда, когда: H содержит единичный элемент из Gсодержит произведение любых двух элементов из H,содержит вместе со всяким своим элементом h обратный к нему элемент 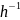 .В случае конечных и, вообще, периодических групп проверка условия 2 является излишней. Всякая подгруппа, отличная от всей группы, называется истинной подгруппой этой группы. Истинная подгруппа некоторой бесконечной группы может быть изоморфна самой группе.Сама группа G и единичная подгруппа называется несобственными подгруппами группы G, все остальные ― собственными. Пересечение всех подгрупп группы G, содержащих все элементы некоторого непустого множества M, называется подгруппой, порожденной множеством M, и обозначается <M>.Если M состоит из одного элемента a, то <a> называется циклической подгруппой элемента a.Группа, совпадающая с одной из своих циклических подгрупп, называется циклической группой.Если группа 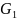  изоморфна некоторой подгруппе H группы G, то говорят, что группа   может быть вложена в группу G.Теоретико-множественное пересечение любых двух (и любого множества) подгрупп группы G является подгруппой группы G.Теоретико-множественное объединение подгрупп, вообще говоря, не обязано являться подгруппой. Объединением подгрупп H и K называется подгруппа, порожденная объединением множеств  .Гомоморфный образ подгрупп ― подгруппа.Если даны две группы и каждая из них изоморфна некоторой истинной подгруппе другой, то отсюда еще не следует изоморфизм самих этих групп.