1.Отношение делимости в кольце целых чисел. Простые числа. Те-ма Евклида. Осн-я теорема арифм-ки.

Рассмотрим отношение делимости в кольце целых чисел. Говорят, что число m делится на n, существует такое целое число k, для которого m = kn.  Число p называется простым, если все его делители несобственные и p>1. Множество простых чисел бесконечно. Теорема Евклида(Простых чисел бесконечно много) Доказательство. Докажем эту теорему методом от противного. Пусть p₁, p₂, …, p_n – все простые числа. Тогда рассмотрим P= p₁* p₂* …*p_n+1. Тогда P не простое, т.к. оно больше любого простого числа. Но оно не составное, т.к. не делится ни на одно из p₁, p₂, …, p_n. Но натуральное число, большее 1 является либо простым, либо составным. Противоречие, значит простых чисел бесконечно много.Основная теорема арифметики: любое целое число можно разложить в произведение простых чисел единственным образом с точностью до порядка и знака множителей :

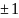2.Нод чисел, его свойства, алгоритм Евклида. Нок чисел.

НОД целых чисел n и m называется наибольшее натуральное число, на которое делятся n и m. НОК является наименьшее натуральное число, которое делится на n и m. Два целых числа называются взаимно простыми, если НОД = 1. НОД(m,n)= НОК(m,n)=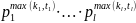

Свойства НОД и НОК:

1)d – общий делитель m и n, НОД(m,n) ;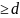

2)K – кратное n и m, НОК(n,m)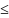 K; 3)m>0, n>0, m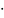 n=НОД(m,n) НОК(n,m);

4)Линейное представление наибольшего общего делителя НОД(m,n)=d=>

=> ; Алгоритм Евклида (поиска НОД) m>n

1)Делим m на n с остатком

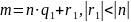
2)n делим на остаток с остатком

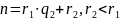
3)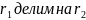 с остатком ….

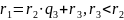k-1)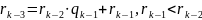

k)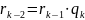 (НОД – последний ненулевой остаток: )

3. Отношение сравнимости целых чисел по модулю данного натурального числа и его свойства. Классы вычетов по модулю m.

Два целых числа a и b сравнимы по модулю натурального числа n (или равноостаточны при делении на n), если при делении на n они дают одинаковые остатки. Число nназывается модулем сравнения.Свойства: Отношение сравнимости по модулю натурального числа   обладает следующими свойствами:

- рефлексивности: для любого целого   справедливо 

- симметричности: если   то 

- транзитивности: если и то

В силу того, что отношение сравнимости по модулю обладает этими тремя свойствами, оно является отношением эквивалентности на множестве целых чисел. Любые два целых числа сравнимы по модулю 1.Если числа a и b

 сравнимы по модулю n, и n делится на m, то a и b сравнимы по модулю m.

Для того, чтобы числа a и b были сравнимы по модулю n, каноническое разложение на простые сомножители которого: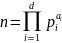 необходимо и достаточно, чтобы Если 

 и  , то  , где .

Множество всех чисел сравнимых с a по модулю n называется классом вычетов a по модулю n, и обычно обозначается   или  . Таким образом, сравнение   равносильно равенству классов вычетов  .

Поскольку сравнение по модулю n является отношением эквивалентности на множестве целых чисел  , то классы вычетов по модулю n представляют собой классы эквивалентности; их количество равно n. Множество всех классов вычетов по модулю n обозначается   или .

Операции сложения и умножения на   индуцируют соответствующие операции на множестве  :