9.Подгруппы. Классы смежности по подгруппе.

Понятие подгруппы Определение Группа называется подгруппой группы , если, во первых (как подмножество) и, во-вторых,

Признак подгруппы: Непустое подмножество H в группе G будет подгруппой этой группы тогда и только тогда, когда: 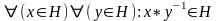.Смежные классы; разложение группы по подгруппе.Условимся о следующих обозначениях. Если A и B два подмножества группы G, то A*B обозначает множество всевозможных произведений элементов первого из них на элементы второго, а - множество всех обратных элементов из A. В этих обозначениях, например, условие, при котором A является подгруппой G можно записать в виде:

Определение Пусть x некоторый фиксированный элемент группы G, а H - любая ее подгруппа. Множество x*H называется левым, а H*x - правым смежным классом группы по подгруппе.

Например, очевидно, что *H=H* =H, так что подгруппа Н сама является одним из смежных классов.

Свойства смежных классов

1. Отображение , определенное формулой является взаимно однозначным для всякого .

2. Каждый элемент x входит в смежный класс x*H.

3. Если y входит в смежный класс x*H , то y*H=x*H

4. Если y не входит в смежный класс x*H, то

(Свойства 1- 4 сформулированы для левых смежных классов, но аналогичными свойствами обладают и правые).

Доказательство.

1. сюръективно по определению смежного класса. Если, то есть , то по закону сокращения , то есть инъективно.

2. Поскольку входит в подгруппу H, x=x* входит в смежный класс x*H.

3. Пусть y=x*h и z , то есть z=y*h^’ Тогда z=(x*h)* h^’= x*(h*h^’) и значит входит в класс x*H. Таким образом, . Обратное включение вытекает из того, что и значит входит в y*H.

4. Докажем от противного. Пусть классы x*H и y*H пересекаются и элемент z входит в каждый из них, так что . Тогда что противоречит нашему предположению.

Следствие

Если подгруппа H конечна, то все левые смежные классы содержат одинаковое число элементов, равное порядку этой подгруппы. (Следует из свойства 1.)

Определение

Индексом [G:H] подгруппы H в группе G называется количество различных левых смежных классов G по H (если оно конечно).

Теорема Лагранжа Если G конечная группа и H ее подгруппа, то

ord(G)={G:H]*ord(H) (Здесь ord( ) обозначает порядок группы).

Доказательство: Пусть - полный перечень левых смежных классов G по H и класс C_i содержит элементы . Тогда m - индекс [G:H] , а n - порядок H (по следствию из предыдущей теоремы). По свойству 3. все элементы X_ij попарно различны и по свойству 2. исчерпывают список элементов группы G. Значит, m*n=ord(G), что и требовалось.

Следствие Порядок подгруппы делит порядок конечной группы.

В самом деле, число ord(G)/ord(H)=[G:H] является целым.

10.Циклические группы.

В теории групп группа (G,∙ ) называется циклической, если она может быть порождена одним элементом a, то есть все её элементы являются степенями a .

Св-ва: Все циклические группы абелевы.Каждая конечная циклическая группа изоморфна группе   —   со сложением по модулю n (её также обозначают  ), а каждая бесконечная — изоморфна Z, группе целых чисел по сложению.В частности, для каждого натурального числа n существует единственная (с точностью до изоморфизма) циклическая группа порядка n.Каждая подгруппа циклической группы циклична.У циклической группы порядка n существует ровно φ(n) порождающих элементов, где φ — функция ЭйлераЕсли p — простое число, то любая группа порядка p циклическая и единственна с точностью до изоморфизма (это следует из теоремы Лагранжа).Прямое произведение двух циклических групп порядков n и m циклично тогда и только тогда, когда n и m взаимно просты.Например, Z₁₂ изоморфна Z_{3 4} , но не изоморфна Z_{6 2}.

Основная теорема о конечнопорождённых абелевых группах утверждает, что любая конечнопорождённая абелева группа единственным образом разлагается в прямое произведение примарных циклических групп. Примарной группой может быть циклическая группа Z_pⁿ, где p — простое число, или Z .Мультипликативная группа любого конечного поля является циклической (она порождается элементом поля наибольшего порядка).Кольцо эндоморфизмов группы Z_n изоморфно кольцу Z_n. При этом изоморфизме числу r соответствует эндоморфизм Z_n, который сопоставляет элементу сумму r его экземпляров. Такое отображение будет биекцией, если и только если r взаимно просто с n, так что группа автоморфизмов Z_n изоморфна  . Утверждение. Каждая подгруппа циклической группы циклична. Доказательство. Пусть G — циклическая группа и H — подгруппа группы G. Если группа G  тривиальна (состоит из одного элемента), то H=G  и H циклична. Если H  — тривиальная подгруппа (состоит из единичного элемента или совпадает со всей группой G), то H циклична. Далее в ходе доказательства будем считать, что G и H не являются тривиальными.