3. Решение этой задачи симплекс-методом необходимо выполнить на компьютере с помощью программы LINPROG.

4. Постановка задачи максимизации ассортиментных наборов.

Обозначим х₃ – количество ассортиментных наборов. Целевая функция будет иметь вид: f₂ = х₃→ max. Ограничения на управляемые параметры х = (х_1, х_2, х₃) будут состоять из ограничений по сырью и по объему выпуска продукции, а также ограничений, связанных с ассортиментными требованиями и для нашего примера запишутся следующим образом:

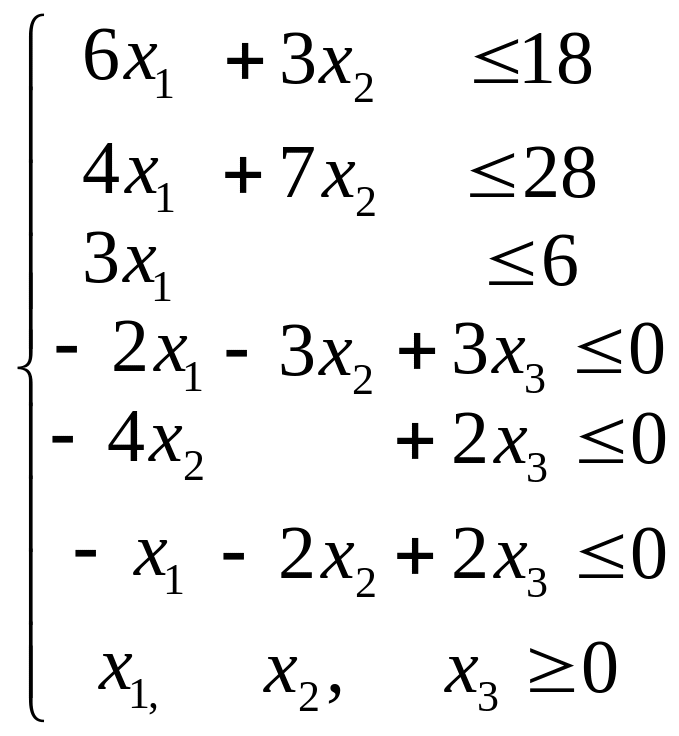
Полученная задача есть задача линейного программирования, т.к. целевая функция и ограничения линейны.

5. Поставленная задача имеет 3 переменных, т.е. графический способ решения не подходит. Для решения задачи симплекс-методом используем программу LINPROG. В результате решения получим x₁ = 1,71, x₂ = 2,57, x₃ = 3,43. Точка Е(1,71; 2,57) расположена на стороне BC многоугольника решений.

Использованная литература

С. В. Жак. Математические модели менеджмента и маркетинга. — Ростов-на-Дону: ЛаПО, 1997.— 320 с.

Варианты заданий:

1. А = , В = , С = (5;7), k₁: k₂: k₃ = 3:4:2

2. А = , В = , С = (5;4), k₁: k₂: k₃ = 4:2:3

3. А = , В = , С = (4;2), k₁: k₂: k₃ = 1:3:2

4. А = , В = , С = (1;7), k₁: k₂: k₃ = 3:1:3

5. А = , В = , С = (5;8), k₁: k₂: k₃ = 4:3:2

6. А = 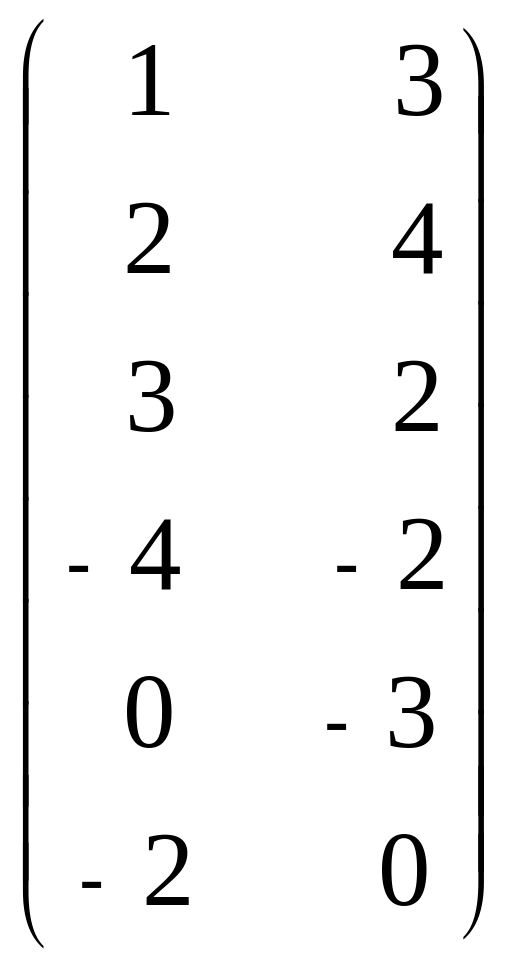, В = , С = (2;3), k₁: k₂: k₃ = 3:2:1

7. А = 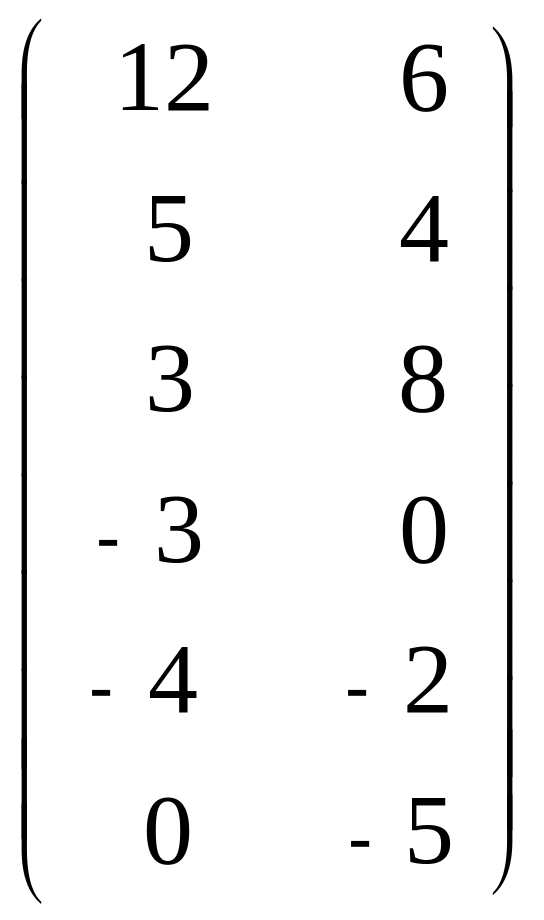, В = , С = (7;12), k₁: k₂: k₃ = 4:4:3

8. А = , В = , С = (4;6), k₁: k₂: k₃ = 2:3:2

9. А = , В = , С = (3;2), k₁: k₂: k₃ = 1:3:2

10. А = , В = , С = (1;3), k₁: k₂: k₃ = 3:2:4

11. А = , В = , С = (1;4), k₁: k₂: k₃ = 1:3:2

12. А = 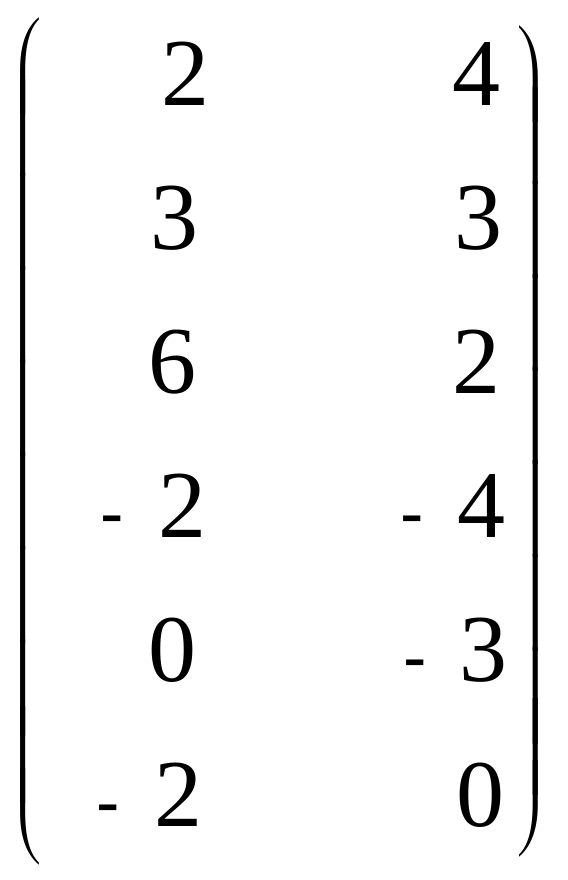, В = , С = (2;4), k₁: k₂: k₃ = 2:3:1

13. А = , В = , С = (4;6), k₁: k₂: k₃= 3:2:4

14. А = 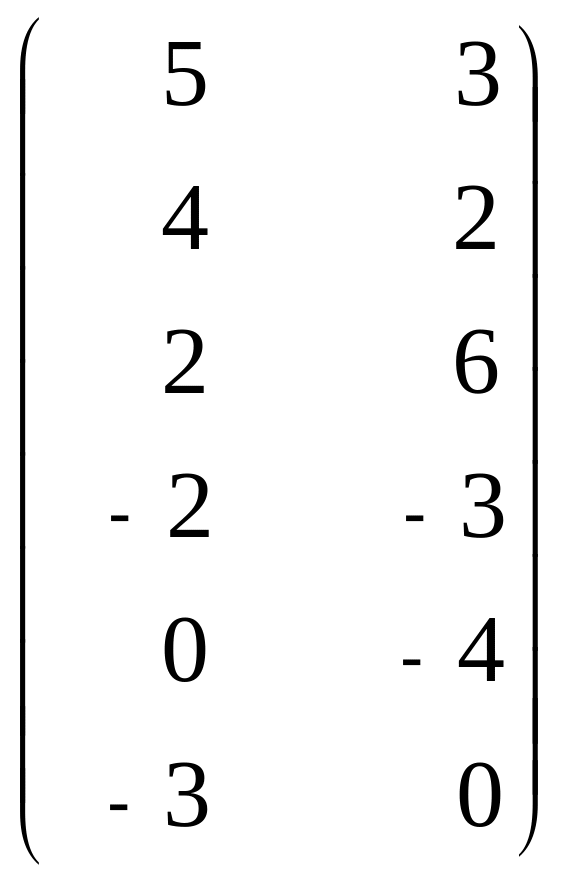, В = , С = (3;2), k₁: k₂: k₃ = 2:3:1

15. А = , В = , С = (7;5), k₁: k₂: k₃ = 1:2:3

16. А = , В = , С = (2;4), k₁: k₂: k₃ = 1:3:2

17. А = 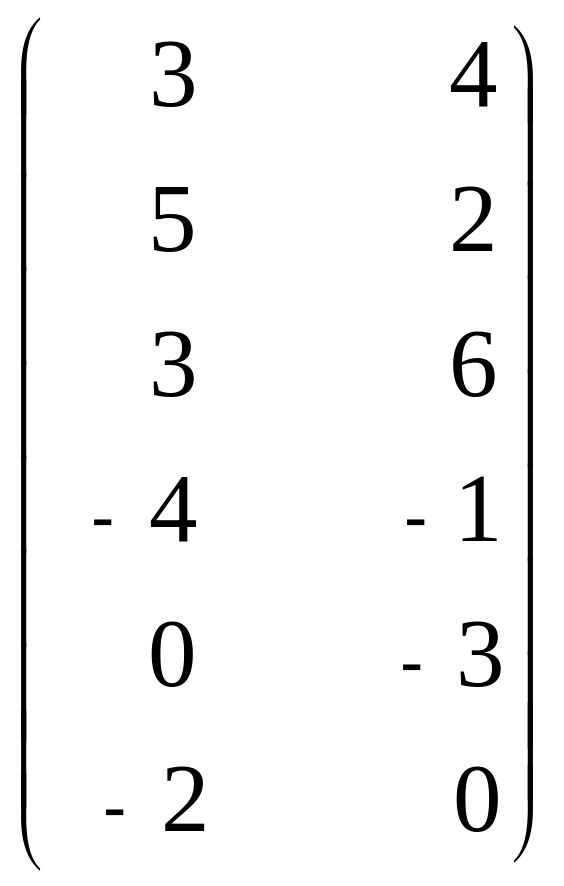, В = , С = (2;7), k₁: k₂: k₃ = 2:4:1

18. А = 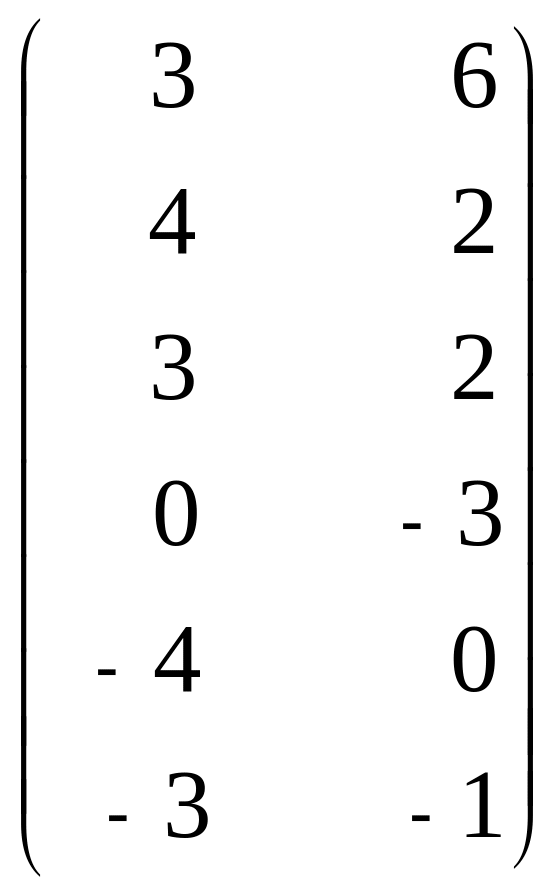, В = , С = (2;3), k₁: k₂: k₃ =3:4:1

19. А = , В = , С = (4;6), k₁: k₂: k₃ =3:5:1

20. А = , В = , С = (5;3), k₁: k₂: k₃ =1:3:2

21. А = , В = , С = (2;6), k₁: k₂: k₃ =3:2:1

22. А = , В = , С = (5;6), k₁: k₂: k₃ =2:4:1

23. А = , В = , С = (3;4), k₁: k₂: k₃ =3:2:4

24. А = , В = , С = (4;5), k₁: k₂: k₃ =3:5:2

25. А = 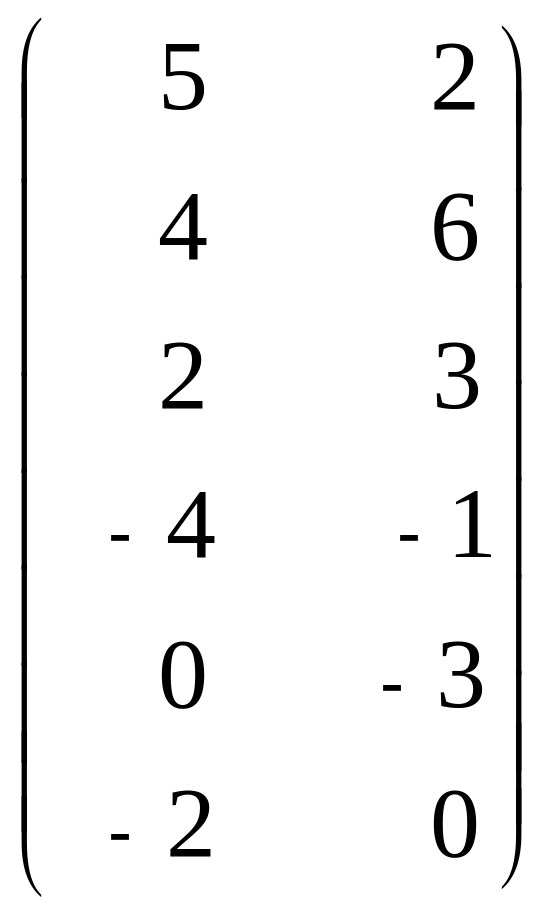, В = , С = (3;4), k₁: k₂: k₃ =2:1:4

26. А = , В = , С = (8;5), k₁: k₂: k₃ =4:3:2

27. А = , В = , С = (2;3), k₁: k₂: k₃ =1:3:2

28. А = , В = , С = (4;6), k₁: k₂: k₃ =2:4:3

29. А = , В = , С = (5;4), k₁: k₂: k₃ =5:1:2

30. А = , В = , С = (2;3), k₁: k₂: k₃ =1:2:3