34. Закопеременые ряды. Абсолютная и условн сходимость

Числ. ряд назыв. знакопеременным, если он содержит как полож., так и отриц. члены

Пусть (1), а (2)

Если ряд 2 сход., то ряд 1 также сход. Если ряд 2 составл. из модулей членов ряда 1, сходится, то ряд 1 назыв. абсолютно сход.

Если ряд 2 расход, а ряд 1 – сход., то говорят, что ряд 1 сходится условно.

Ряд называется абсолютно схяодящимся, если сходится ряд .

Ряд называется условно сходящимся, если он сходится, а ряд   расходится.

35. Знакочередующие ряды. Признак Лейбница.

(3) – закочередующийся ряд.(частный случай знака переменного ряда)

Признак Лейбница:

Если для знакочеред. ряда 3 выполн. условие:

1.

2.

то ряд 3 сход., при этом его сумма S≤a1, а остаток ряда

36.Понятие степенного ряда. Обл сходимости степенного ряда.

Ряд, членами которого являются степенные функции аргумента x, называется степенным рядом:

Часто рассматривается также ряд, расположенный по степеням (x − x0), то есть ряд вида

де x0 − действительное число.

Областью сходимости степенного ряда называется множество тех значений х, при которых степенной ряд сходится.

37. Теорема Абеля

(4)

1)Если степенной ряд сходится при х=х0, u≠0,то он сходится абсолютно при всех |x|<|x0|

2)если при х=х1 степенн ряд расход,то он расход при всех |x|>|x1|

Если ряд 4 сход. в некот. т. х1≠0, то он будит сход. при всех знач.-ях х принадлеж. R. |x|<|x1|.

Если ряд 4 расход, в x2, то он будит расходящимся и при всех х принадлеж. R, |x|>|x2|.

38. Ряды Тейлора и Маклорена

Пусть f(x) имеет производные всех порядков некотор. окрестн. т. x. Рядом Тейлора для f(x) в т. х0 назыв. степен. ряд след. вида:

Если х0=0, то ряд 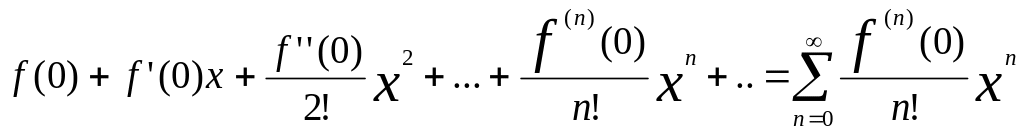назыв. рядом Маклорена

При выполнении некотр. условий ряд Тейлора для f(x) равен самой f(x). Говорят, что ф-ия представима в виде ф-ии степен. ряда

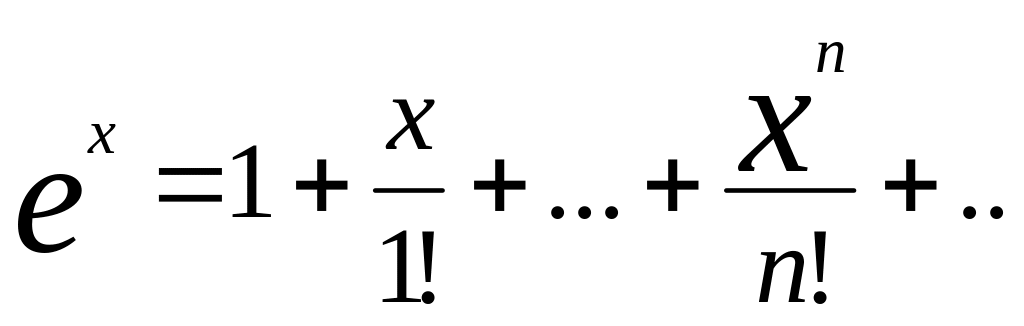x принадлеж. R.

3. Разложение функции y=cosx в ряд Маклорена. Дифференцируя ряд (33), получаем разложение при x (-∞;+∞):

cosx=1- .

4/Разложить в ряд Маклорена функцию f(x)=ln(1+x).

Проинтегрируем обе части равенства (37) от 0 до x при x (-1;1). Получим

или

ln(1+x)=x .

Можно показать, что ряд имеет область сходимости (-1;1].

39. Разложение ф-ий sinx, cosx, e^x, ln(1+x) в ряд Маклорена

Разложение функции f(x)=ex в ряд Маклорена.

f(x)=f′(x)=f″(x)=…=f(n)(x)=…=ex.

f(0)=f′(0)=f″(0)=…=f(n)(0)=…=1.

Составим для функции f(x)=ex формально ряд Маклорена: 1+

Найдём области сходимости этого ряда.

при любых x, следовательно, областью сходимости ряда является промежуток (-∞;+∞). Заметим, что так как ряд сходится абсолютно, то при любых х и тем более при любых х. Так как f^(n+1)(x)=ex и f^(n+1)(с)=e^с, то =e^c=0. Таким образом, имеет место разложение при x(-∞;+∞)

e^x=1+ .

Разложение функции f(x)=sinx в ряд Маклорена.

Вычислим производные данной функции.

f′(x)=cosx=sin(x+ ), f″(x)=-sinx=sin(x+ ),

f″′(x)=-cosx=sin(x+ ), f(4)(x)=sinx=sin(x+ ), …, f(n)(x)=sin(x+ ), … . Вычислим значения f(x) и производных в точке 0: f(0)=0, f′(0)=1, f″(0)=0, f″′(0)=-1, f^(4)(0)=0, …, f^(2n-1)(0)=(-1)^n-1, f^(2n)(0)=0.

Исследуем остаточный член ряда.

|Rn(x)|= = так как |sin(c+(n+1) |≤1. Переходя к пределу при n→∞, получаем следовательно, и . Рекомендуем показать самостоятельно, что областью сходимости ряда является промежуток (-∞;+∞). Таким образом, имеет место разложение при x (-∞;+∞):

sinx=x- .