30.Понятие числовогоряда и суммы ряда. Геометрическаяпрогрессия.

Числовым рядом назыв. выражение вида а1+а2+…+аn+…, кот. можно записать (1)

а1, а2 – члены ярда

аn – общий член ряда или n-ый член ряда

Сумма n-первых членов ряда Sn=a1+a2+..+an назыв. n-ой частичной суммой ряда.

Числовой ряд назыв. сходящимся, если сущ. конечн. предел последоват. Sn=S, S принадлеж. R, S - сумма ряда. Если lim nбескон S не существует,то ряд наз расходящимся

Ряд геометрической прогрессии

Исследуем сходимость ряда

который называется рядом геометрической прогрессии. Ряд часто используется при исследовании рядов на сходимость.

31.Простейшие свойства сходящихся рядов. Необходимый признак сходимости ряда.

Св-ва сход. рядов:

1. если ряд сходится и имеет сумму S,то ряд с,то такой также сходится и имеет сумму c*S

2. сходимость ряда не нарушается, если произвольным образом изменить (добавить, отбросить) конечное число членов ряда

3. сход. ряда можно почленно умножить на любое число, т.е. общий член множителей можно вынести за знак скобку ,

3. сход. ряды можно почленно складывать и отнимать

, ,

4/ сумма сходящегося ряда можно представить в виде суммы частичной суммы рядов и его остатка

5) Если ряд сходится, то

Необх признак

Если ряд - сход., то

Док-во:

, ,

Данный признак означает, что если то ряд расходится. Но условие явл необходим,но недостаточным,т.е из выполн данных услов не всегда следует сходимость рядов

32.Интегральный признак сходимости

Интегральный признак Коши-Маклорена — признак сходимости убывающего положительного числового ряда. Признак Коши-Маклорена даёт возможность свести проверку сходимости ряда к проверке сходимости несобственного интеграла соответствующей функции на , последний часто может быть найден в явном виде.

Формулировка теоремы

Пусть для функции f(x) выполняется:

1) (функция принимает неотрицательные значения)

2. (функция монотонно убывает)

3.

Тогда ряд и несобственный интеграл сходятся или расходятся одновременно.

33. Признак сравнения для положительных рядов.Признаки Даламбера и Коши

Пусть даны 2 ряда: (1), (2), an, bn≥0

Признаки сравнения:

Пусть для членов рядов (1) и (2) выполн. неравенство an≤bn, для любых натур чисел, тогда: Если ряд (2) сход., то ряд (1) также сход. , если ряд (1) расх., то (2) расх. тоже

Пусть дял членов рядов (1) и (2) выролн. условие: , А приндлеж. R A≠0, тогда ряды (1) и (2) сх. или расх. одновременно

Признак Д’Аламбера:

(1) , an>0, 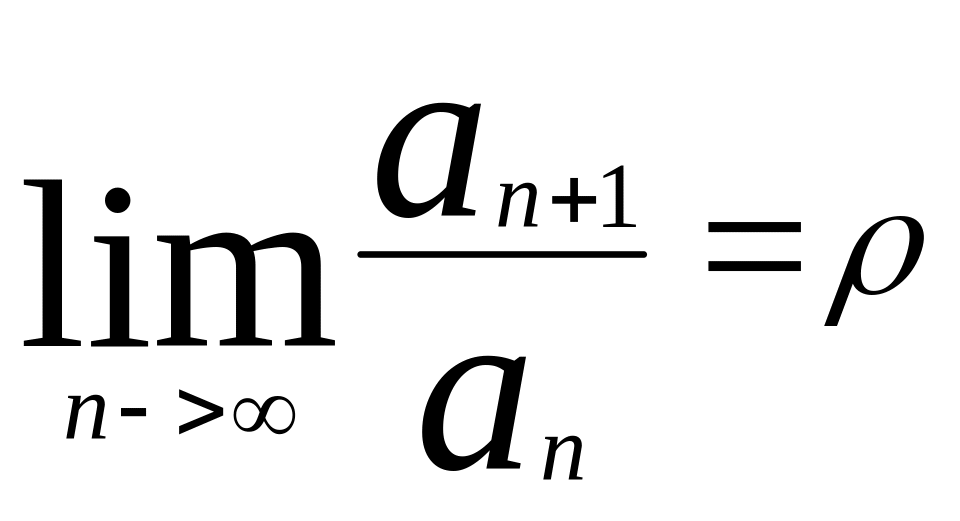, тогда:

Если <1, то ряд 1 сход., Если >1, то ряд 1 расх. , Если =1, то признак не срабатывает

Признак Коши:

1. Если для ряда 1 сущ. 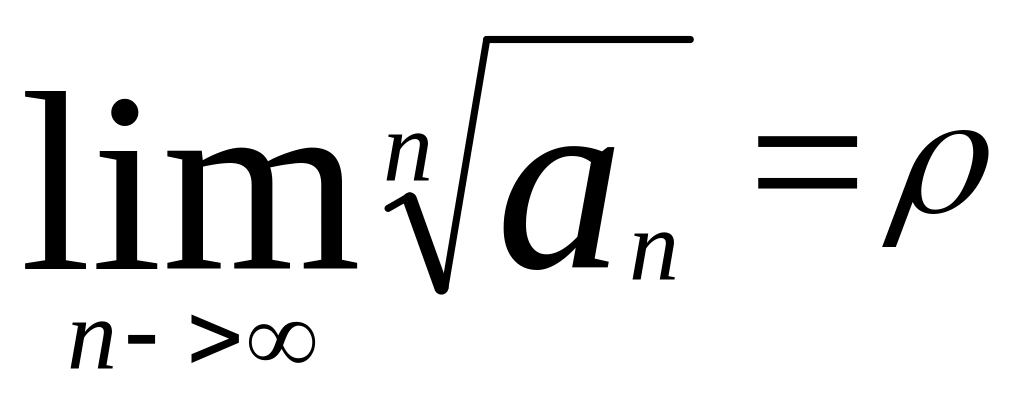, то при <1, ряд 1 сх, а при >1, ряд 1 расх.

2. Интегральный признак Коши: если для ряда 1 с положит. членами выполн условия:

1)

2) сущ. непрерыв. невозраст. ф-ия f(x): an=f(n) для любых натур. n, то ряд 1 инесобств. интеграл сход. или расх одновременно:

α>1 – сход, α<1 – расх.