matematika_konferentsia (2)

Система линейных алгебраических уравнений

Системой m линейных уравнений с n неизвестными называется система вида:

где aij и bi (i=1,…,m; b=1,…,n) – некоторые известные числа, а x1,…,xn – неизвестные. В обозначении коэффициентов aij первый индекс i обозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.

Коэффициенты при неизвестных будем записывать в виде матрицы , которую назовём матрицей системы.

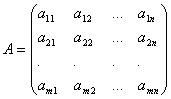
Числа, стоящие в правых частях уравнений, b₁,…,b_m называются свободными членами.

Совокупность n чисел c₁,…,c_n называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c₁,…,c_n вместо соответствующих неизвестных x₁,…,x_n.

Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:

1. Система может иметь единственное решение.

2. Система может иметь бесконечное множество решений. Например,

,

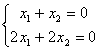решением этой системы является любая пара чисел, отличающихся знаком.

3. И третий случай, когда система вообще не имеет решения. Например,

,

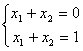если бы решение существовало, то x₁ + x₂ равнялось бы одновременно нулю и единице.

Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной.

Рассмотрим один из способов нахождения решений системы.

Метод Зейделя для решения СЛАУ

Приведение системы к виду, удобному для итераций. Для того чтобы применить метод Зейделя к решению системы линейных алгебраических уравнений

Ax = b

с квадратной невырожденной матрицей A, необходимо предварительно преобразовать эту систему к виду

x = Bx + c.

Здесь B – квадратная матрица с элементами b_ij (i, j = 1, 2, …, n), c – вектор-столбец с элементами c_ij (i = 1, 2, …, n).

В развернутой форме записи система имеет следующий вид:

x₁ = b_11x1 + b_12x2 + b_13x3 + … + b_1nxn + c₁

x₂ = b_21x1 + b_22x2 + b_23x3 + … + b_2nxn + c₂

. . . . . . . . . . . . . . . . .

x_n = b_n1x1 + b_n2x2 + b_n3x3 + … + b_nnxn + c_n

Вообще говоря, операция приведения системы к виду, удобному для итераций, не является простой и требует специальных знаний, а также существенного использования специфики системы.

Самый простой способ приведения системы к виду, удобному для итераций, состоит в следующем. Из первого уравнения системы выразим неизвестное x1:

x₁ =а_11–1 (b₁ – a_12x2 – a_13x3 – … – a_1nxn),

из второго уравнения – неизвестное x2:

x₂ = _a21–1 (b₂ – a_22x2 – a_23x3 – … – a_2nxn),

и т. д. В результате получим систему

x₁ = b_12x2 + b_13x3 +… + b_{1,n–1xn–1} + b_1nxn+ c₁ ,

x₂ = b_21x1 + b_23x3 +… + b_{2,n–1xn–1} + b_2nxn+ c₂ ,

x₃ = b_31x1 + b_32x2 + … + b_{3,n–1xn–1} + b_3nxn+ c₃ ,

. . . . . . . . . . . . . . . . . . . . . . .

x_n = b_n1x1 + b_n2x2 +b_n3x3 +… + b_{n,n–1xn–1} + c_n ,

в которой на главной диагонали матрицы B находятся нулевые элементы. Остальные элементы выражаются по формулам

b_ij = –a_ij / a_ii, c_i = b_i / a_ii (i, j = 1, 2, …, n, j ≠ i)

Конечно, для возможности выполнения указанного преобразования необходимо, чтобы диагональные элементы матрицы A были ненулевыми.

Описание метода. Введем нижнюю и верхнюю треугольные матрицы

0 0 0 … 0 0 b₁₂ b₁₃ … b_1n

b₂₁ 0 0 … 0 0 0 b₂₃ … b_2n

B₁ = b₃₁ b₃₂ 0 … 0 , B­­₂ = 0 0 0 … b_3n

. . . . . . . . . . . . . .

b_n1 b_n2 b_n3 …0 0 0 0 … 0

Заметим, что B = B₁ + B₂ и поэтому решение x исходной системы удовлетворяет равенству

x = B_1x + B_{2 x} + c .

Выберем начальное приближение x(0) = [x₁(0), x₂(0), …, x_n(0)]^T. Подставляя его в правую часть равенства при верхней треугольной матрице B₂ и вычисляя полученное выражение, находим первое приближение

x(1) = B_1x(0) + B_2x(1)

Подставляя приближение x(1), получим

x(2) = B_1x(1) + B_2x(2)

Продолжая этот процесс далее, получим последовательность x(0), x(1), …, x(n), … приближений к вычисляемых по формуле

x(k+1) = B₁(k+1) + B₂(k) + c

или в развернутой форме записи

x₁^(k+1) = b₁₂x₂^(k) + b₁₃x₂^(k) + … + b_1nx_n^(k) + c₁ ,

x₂^(k+1) = b₂₁x₁^(k+1) + b₂₃x₃^(k) + … + b_2nx_n^(k) + c₂ ,

x₃^(k+1) = b₃₁x₁^(k+1) + b₃₂x₂^(k+1) + … + b_3nx_n^(k) + c₃ ,

. . . . . . . . . . . . . . . . . . . . . . . . . .

x_n^(k+1) = b_n1x₁^(k+1) + b_n2x₂^(k+1) + b_n3x₃^(k+1) + … + c_n .

Объединив приведение системы к виду, удобному для итераций и метод Зейделя в одну формулу, получим

xi(k+1) = xi(k) – aii–1(∑j=1i–1 aijxj(k+1) + ∑j=1n aijxi(k) – bi).

Тогда достаточным условием сходимоти метода Зейделя будет

∑j=1, j≠i n | a-ij | < | a-ii |

(условие доминированния диагонали).

Метод Зейделя иногда называют также методом Гаусса-Зейделя, процессом Либмана, методом последовательных замещений.

Этот метод является модификацией метода простых итераций и в некоторых случаях приводит к более быстрой сходимости.

Итерации по методу Зейделя отличаются от простых итераций тем, что при нахождении i-й компоненты (k+1)-го приближения сразу используются уже найденные компоненты (к +1) -го приближения с меньшими номерами . При рассмотрении развернутой формы системы итерационный процесс записывается в виде

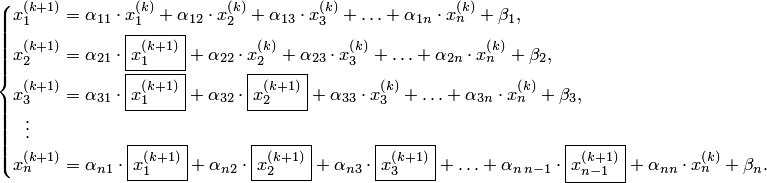
Теорема о достаточном условии сходимости метода Зейделя. Если для системы  какая-либо норма матрицы меньше единицы, т.е. , то процесс последовательных приближений (10.15) сходится к единственному решению исходной системы при любом начальном приближении .

Записывая (1) в матричной форме, получаем

(2)

где являются разложениями матрицы

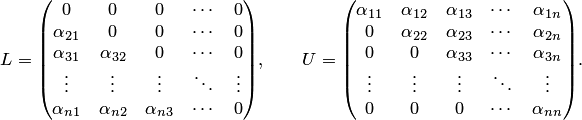
Преобразуя (2) к виду , получаем матричную форму итерационного процесса метода Зейделя:

(3)

Тогда достаточное, а также необходимое и достаточное условия сходимости будут соответственно такими:

(4)

Замечания :

1. Для обеспечения сходимости метода Зейделя требуется преобразовать систему к виду с преобладанием диагональных элементов в матрице А (метод простых итераций).

2. Процесс (2) называется последовательным итерированием, так как на каждой итерации полученные из предыдущих уравнений значения подставляются в последующие. Как правило, метод Зейделя обеспечивает лучшую сходимость, чем метод простых итераций (за счет накопления информации, полученной при решении предыдущих уравнений). Метод Зейделя может сходиться, если расходится метод простых итераций, и наоборот.

3. Преимуществом метода Зейделя, как и метода простых итераций, является его "самоисправляемость".

4. Метод Зейделя имеет преимущества перед методом простых итераций, так как он всегда сходится для нормальных систем линейных алгебраических уравнений, т.е. таких систем, в которых матрица А является симметрической и положительно определенной. Систему линейных алгебраических уравнений с невырожденной матрицей А всегда можно преобразовать к нормальной, если ее умножить слева на матрицу . Система является нормальной.

Алгоритм метода Зейделя

1. Преобразовать систему к виду одним из описанных способов.

2. Задать начальное приближение решения произвольно или положить , а также малое положительное число (точность). Положить .

3. Произвести расчеты по формуле (1) или (2) и найти .

4. Если выполнено условие окончания , процесс завершить и в качестве приближенного решения задачи принять . Иначе положить и перейти к пункту 3.

Пример. Методом Зейделя с точностью решить систему линейных алгебраических уравнений:

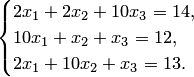
Решение. 1. Приведем систему к виду :

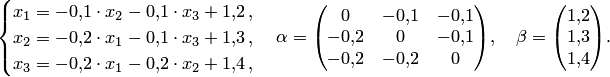
Так как , условие сходимости выполняется.

2. Зададим . В поставленной задаче .

Выполним расчеты по формуле (1):

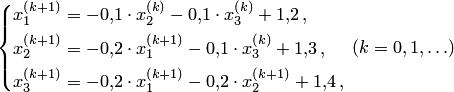
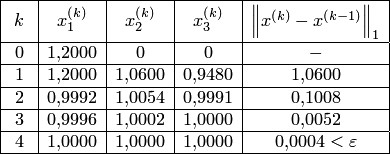
Очевидно, найденное решение является точным.

4. Расчет завершен, поскольку выполнено условие окончания .