Билет №2.

1.) 1.) Различные формы записи задач линпрогр-ния:

1)Координатная форма записи задач:

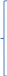Z(x)=c1x1+c2x2+…+cnxn → max (min)

a11x1+a12x2+…+a1nxn=b1

a21x1+a22x2+…+a2nxn=b2

…………………………

am1x1+am2x2+…+amnxn=bm

xi ≥ 0

Или:

Z(x)=Σcixi → max(min)

Σ aijxj=bi

xj≥0

2)Векторная форма записи задач:

Х=(х1, х2,…хn)

C=(c1, c2,…cn)

a11 b1

A1 = a21 ; B = b2

… …

am1 bm

Z(x) = C*X → max (min)

A1x1+A2x2+...+Anxn=B

X ≥ 0

3) Матричная форма записи:

a11 а12…a1n

а21 а22….а2n

A= ………

am1 am2…amn

Z(x) = C*X → max (min)

A*X=B

X ≥ 0

Приведение общей задачи ЛП к канон.форме:

(1) a1x1+a2x2+…+anxn ≤ b1

прибвим xn+1 так, чтобы лев.часть стала равна пр.ч.

a1x1+a2x2+…+anxn+ xn+1 = b1, где xn+1= b1 - a1x1 - a2x2 -…- anxn (xn+1-дополн.перем.)

Теорема. Каждому решению ß(β1…βn) нер-ва (1) соотв.единств.реш-е след.сис-мы:

a1x1+a2x2+…+anxn+ xn+1 = b1 (2)

xn+1≥ 0

Каждому реш-ю сис-мы (2) соотв.единств.реш-е нер-ва (1)

Док-во:1) пусть ß – реш-е нер-ва

a1β1+a2β2+…+anβn ≤ b1 (3)

0≤b1-a1β1-a2β2-…-anβn = βn+1

Если подст. βi в (2) вместо xi:

a1β1+a2β2+…+anβn+(b1-a1β1-a2β2-…-anβn)=b1

b1=b1

2) a1β1+a2β2+…+anβn+ βn+1=b1 (4)

βn+1≥0

Отбросим βn+1 из (4). Т.к. βn+1 – неотриц., отбросив ее, получим нер-во (3).

Замечание. Дополн.неизвест.не влияют на цел.ф-ю (т.е.вводятся с коэф-м 0).

Замечание. В зав-ти от знака нер-вадополн.перем.надо либо прибав., либо вычит.

2.) Фундаментальная система решений однородной системы уравнений, теорема об её существовании. Векторная форма записи общего решения неоднородной системы уравнений.Фундаментальной системой решений однородной системы уравнений называется линейно независимая система векторов-решений системы F₁, F₂, … F_k, по которой разлагается любое решение системы, т.е. любое решение системы уравнений равно X=F₁t₁+F₂t₂+…+F_kt_k, где t₁, t₂, … t_k – вещественные числа. Т. Если ранг матрицы системы однородных уравненийr меньше числа неизвестных n, то система уравнений имеет фундаментальную систему решений, состоящую из nr векторов-решений. Док: Пусть система записана в виде 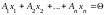. Если ранг матрицы системы равен r(r(A)=r), то равносильная разрешенная система уравнений содержит r уравнений и имеет вид 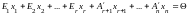. Т. к.n>r, то система имеет n –rсвободных неизвестных 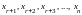. Задав свободным неизвестным значения 0 и 1, можно найти n –rчастных решений вида , , 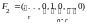…, 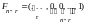. В этих векторах вместо значений базисных переменных поставлены точки, так как они в данном рассмотрении не имеют значения. Покажем, что 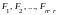образуют фундаментальную систему решений. 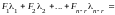Чтобы доказать, что данные векторы являются линейно независимыми, составим линейную комбинацию 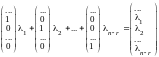.Данная линейная комбинация равна нулевому вектору только при 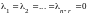. Это и подтверждает линейную независимость векторов. Покажем, что любое решение системы уравнений 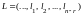является линейной комбинацией . 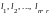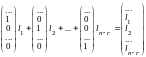Составим вектор К, являющийся линейной комбинацией векторов с коэффициентами .Решения L и K при одних и тех же разрешенных неизвестных имеют одинаковые свободные неизвестные, следовательно, они совпадают (L= K), т. е. .

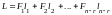Векторная форма записи общего решения неоднородной сис-мы ур-ний. Т. Общее решение неоднородной системы уравнений АХ=В равняется сумме частного решения этой системы К и линейной комбинации решений фундаментальной системы решений соответствующей однородной системы АХ=0, т.е. Х=К+ F₁t₁+F₂t₂+…+F_kt_k, где К - какое-либо решение неоднородной системы уравнений АХ=В, F₁, F₂, … F_k – фундаментальная система решений однородной системы уравнений, t₁, t₂, … t_k– произвольно заданные числа. Док-во: 1. Подставим X=К+F₁t₁+F₂t₂+…+F_kt_k в уравнение АХ=В, получим AX=A(К+F₁t₁+F₂t₂+…+F_kt_k)=AK+AF₁t₁+AF₂t₂+…+AF_kt_k=B+©t₂+…+©t_k=B, так как векторы F₁, F₂, … F_k являются решениями однородной системы АХ=©. Значит, Х является решением системы АХ=В. 2.Покажем, что любое решение уравнения АХ=В имеет вид L= К+ F₁t₁+F₂t₂+…+F_kt_k. Пусть К – некоторое частное решение уравнения АХ=В, L – любое другое ршение этого уравнения. Разность эти решений (L-K) является решением одного уравнения AX=©. Действительно, A(L-K)=AL-AK=B-B=0. Поэтому L-K является линейной комбинацией векторов-решений фундаментальной системы однородной системы уравнений, т.е. L-K= F₁t₁+F₂t₂+…+F_kt_k.