
1.) Преобразование целевой функции при переходе от одного опорного решения к другому. Теорема об улучшении опорного решения, её следствия.
Пусть
 опорное решение задачи линейного
программирования c
базисом
опорное решение задачи линейного
программирования c
базисом
 .
Значение целевой функции задачи на
этом решении равно
.
Значение целевой функции задачи на
этом решении равно
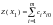 .
Перейдем к другому опорному решению:
.
Перейдем к другому опорному решению:
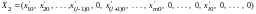
с базисом
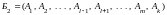 .
Значение целевой функции на этом решении
.
Значение целевой функции на этом решении
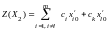 .
Формулы пересчёта правых частей
уравнений:
.
Формулы пересчёта правых частей
уравнений:
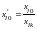 ;
;
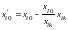 ;
i = 1, 2, …, m;
i
l. Получим:
;
i = 1, 2, …, m;
i
l. Получим:

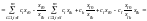
 ,
т.е.
,
т.е.
 .
Находим приращение целевой функции
при переходе от одного опорного решения
к другому
.
Находим приращение целевой функции
при переходе от одного опорного решения
к другому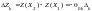 .
.
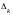 - оценка разложения вектора условий
по
базису опорного решения и
вычисляемая по формуле
- оценка разложения вектора условий
по
базису опорного решения и
вычисляемая по формуле
 ,
,
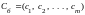 вектор коэффициентов
целевой функции при базисных переменных,
вектор коэффициентов
целевой функции при базисных переменных,
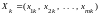 вектор коэффициентов
разложения вектора
по базису опорного решения,
вектор коэффициентов
разложения вектора
по базису опорного решения,
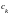 коэффициент целевой
функции при переменной
.
Т. Если в задаче линейного
программирования на максимум (минимум)
хотя бы для одного вектора условий
оценка разложения по базису невырожденного
опорного решения отрицательная
(положительная), то опорное решение
может быть улучшено, т.е. можно найти
новое опорное решение, на котором
значение целевой функции будет больше
(меньше). Док-во. Пусть решается задача
на максимум, которая имеет невырожденное
опорное решение
коэффициент целевой
функции при переменной
.
Т. Если в задаче линейного
программирования на максимум (минимум)
хотя бы для одного вектора условий
оценка разложения по базису невырожденного
опорного решения отрицательная
(положительная), то опорное решение
может быть улучшено, т.е. можно найти
новое опорное решение, на котором
значение целевой функции будет больше
(меньше). Док-во. Пусть решается задача
на максимум, которая имеет невырожденное
опорное решение
 ,
,
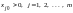 ,
и
,
и
 .
Перейдем к новому опорному решению
.
Перейдем к новому опорному решению
 ,
введём в базис вектор
,
введём в базис вектор
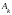 и исключим из базиса вектор
и исключим из базиса вектор
 .
Приращение целевой функции
.
Приращение целевой функции
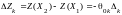 .
Так как
.
Так как
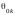 > 0,
,
то
> 0,
,
то
 .
Следовательно, значение целевой функции
на новом опорном решении
будет больше, чем на первом
.
Следовательно, значение целевой функции
на новом опорном решении
будет больше, чем на первом
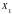 .
Следствие 1. Для наибольшего
изменения целевой функции при улучшении
опорного решения необходимо выбор
вектора выводимый из базиса (с номером
l) и вводимого в
базис (с номером k)
производить из условий: 1. в задаче на
максимум
.
Следствие 1. Для наибольшего
изменения целевой функции при улучшении
опорного решения необходимо выбор
вектора выводимый из базиса (с номером
l) и вводимого в
базис (с номером k)
производить из условий: 1. в задаче на
максимум
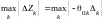 ;
2. в задаче на минимум
;
2. в задаче на минимум
 .
Следствие 2. Опорное решение задачи
линейного программирования на максимум
(минимум) является оптимальным, если
для любого вектора условий оценка
разложения по базису опорного решения
неотрицательная (неположительная),
т.е. в задаче на максимум
.
Следствие 2. Опорное решение задачи
линейного программирования на максимум
(минимум) является оптимальным, если
для любого вектора условий оценка
разложения по базису опорного решения
неотрицательная (неположительная),
т.е. в задаче на максимум
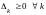 ;
в задаче на минимум
;
в задаче на минимум
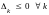 .
Следствие 3.
Оптимальное решение задачи линейного
программирования является единственным,
если для любого вектора условий, не
входящего в базис, оценка отлична от
нуля, т.е. в задаче на максимум
.
Следствие 3.
Оптимальное решение задачи линейного
программирования является единственным,
если для любого вектора условий, не
входящего в базис, оценка отлична от
нуля, т.е. в задаче на максимум
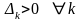 ;
в задаче на минимум
;
в задаче на минимум
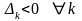 .
.
Следствие 4. Задача линейного
программирования имеет бесконечное
множество оптимальных решений, если
она имеет оптимальное решение, при
котором хотя бы один из векторов
условий, не входящих в базис оптимального
решения, имеет оценку равную нулю,
т.е.
k
{m+1, m+2,
..., n}:
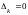 .
.
Следствие 5. Задача линейного
программирования не имеет решения
ввиду неограниченности целевой
функции, если для какого-либо из
векторов условий
с оценкой
,
противоречащей признаку оптимальности,
среди коэффициентов разложения по
базису опорного решения нет
положительного, т.е. в задаче на максимум
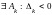 и
и
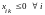 ;
в задаче на минимум
;
в задаче на минимум
 и
.
и
.
2.) Теорема
о двух системах векторов, которым
соответствуют равносильные системы
уравнений. Алгоритм нахождения базиса.
Т.Если двум системам векторов
А1,А2, …, Аn
и В1,В2,…,Вn
соответствуют равносильные системы
уравнений А1х1+А2х2+…+Аnxn=
Θ, B1х1+В2х2+…+Вnxn=
Θ, и векторы В1,В2,…,Вr
образуют базис системы, то
соответствующие векторы А1, А2,…,Аr
образуют базис системы и при этом
разложения соответствующих векторов
систем по своим базисам совпадают, т.е.
Вj=B1
ƛ1j+B2
ƛ2j+…+Br
ƛrj (j=r+1,
2,…, n), то Aj=A1
ƛ1j+A2
ƛ2j+…+Ar
ƛrj (j=r+1,
2,…,n). Док-во. Пусть
В1,В2,…,Вr
(r≤n)
базис системы векторов (2). Покажем, что
А1, А2,…,Аr
линейно зависимы, т.е. есть ненулевой
набор ƛ1, ƛ2, …, ƛr,что
А1 ƛ1+А2 ƛ2+…+ Ar
ƛr= Θ. А1 ƛ1+А2
ƛ2+…+ Ar
ƛr+ Ar+10+
Ar+20+…+
An0=
Θ. B1 ƛ1+B2
ƛ2+…+Br
ƛr+Br+10+Br+20+…+Bn0=
Θ или B1 ƛ1+B2
ƛ2+…+Br
ƛr= Θ при ненулевом
наборе чисел ƛ1, ƛ2, …, ƛr,
что возможно только при линейной
зависимости векторов В1,В2,…,Вr.
Это противоречит условию теоремы.
Следовательно, А1, А2,…,Аr
линейно независимые. Вj=B1
ƛ1j+B2
ƛ2j+…+Br
ƛrj (j=1,
2,…, n). Покажем, что с такими
же коэффициентами ƛ1j,
ƛ2j,…, ƛrj
разлагается Aj
по векторам А1, А2,…,Аr
. B1 ƛ1+B2
ƛ2+…+Br
ƛr+Br+10+Br+20+…+Bj-10-Bj∙1+Bj+10+…+
Bn0= Θ
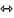 A1 ƛ1+A2
ƛ2+…+Ar
ƛr+Ar+10+Ar+20+…+Aj-10-Aj∙1+Aj+10+…+
An0=
Θ, Aj=
ƛ1+A2 ƛ2+…+Ar
ƛr (j=1,
2,…, n). Алгоритм нахождения
базиса. 1) составить соответствующую
системе векторов однородную систему
уравнений А1х1+А2х2+…+Аnxn=
Θ; 2)привести эту систему к равносильной
разрешенной системе вида
E1x1+E2x2+…+Erxr+A’r+1xr+1+…+A’jxj+…+A’nxn=
Θ; 3) записать базис системы векторов
Б=(А1, А2,…,Аr);
4) записать разложения векторов по
базису; коэффициентами разложения
вектора Aj
по этому базису являются координаты
соответствующего вектора A’j=
(a’1j,
a’2j,…,a’rj)
в разрешенной системе уравнений, т.е.
A’j=А1
a’1j,
А2 a’2j,…,
Аr a’rj
(j=1, 2, …, n).
Система векторов, состоящая из n
векторов, ранг которой равен r,
может иметь несколько базисов. Число
возможных базисов системы векторов
определяется как число сочетаний из n
по r по формуле
A1 ƛ1+A2
ƛ2+…+Ar
ƛr+Ar+10+Ar+20+…+Aj-10-Aj∙1+Aj+10+…+
An0=
Θ, Aj=
ƛ1+A2 ƛ2+…+Ar
ƛr (j=1,
2,…, n). Алгоритм нахождения
базиса. 1) составить соответствующую
системе векторов однородную систему
уравнений А1х1+А2х2+…+Аnxn=
Θ; 2)привести эту систему к равносильной
разрешенной системе вида
E1x1+E2x2+…+Erxr+A’r+1xr+1+…+A’jxj+…+A’nxn=
Θ; 3) записать базис системы векторов
Б=(А1, А2,…,Аr);
4) записать разложения векторов по
базису; коэффициентами разложения
вектора Aj
по этому базису являются координаты
соответствующего вектора A’j=
(a’1j,
a’2j,…,a’rj)
в разрешенной системе уравнений, т.е.
A’j=А1
a’1j,
А2 a’2j,…,
Аr a’rj
(j=1, 2, …, n).
Система векторов, состоящая из n
векторов, ранг которой равен r,
может иметь несколько базисов. Число
возможных базисов системы векторов
определяется как число сочетаний из n
по r по формуле
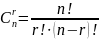
Билет №9
1.) Метод искусственного базиса решения задач линейного программирования, его обоснование. Леммы и теорема об оптимальности опорного решения. Метод искусственного базиса применяется в том случае если, задача не имеет начального опорного решения с базисом из единичных векторов. 1.Составляем расширенную задачу. (добавляем искусственные переменные – не отрицательные переменные которые вводятся в левую часть одного из уравнений системы ограничений с коэф. +1 и в целевую функцию на макс. -М в задаче на минимум +М). 2.Либо находим оптимальное решение, либо устанавливаем его отсутствие.
Особенности: 1.Оценки разложений
векторов условий ∆j = Сб * Xj –
cj состоят из двух слагаемых. Одно
из которых не зависит от М. На первом
этапе расчета, используем только
слагаемые оценок ∆J(M). 2.Векторы
соответствующие иск. Переменным, которые
выводятся из базиса, исключаем из
рассмотрения. 3.Далее продолжаем
симплексным методом с использованием
оценок независящих от М. Лемма.
Любому допустимому решению
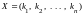 исходной задачи соответствует
допустимое решение расширенной задачи
исходной задачи соответствует
допустимое решение расширенной задачи
 и, наоборот, любому допустимому
решению
расширенной задачи
соответствует допустимое решение
исходной задачи
.
При этом значения целевых функций
задач на соответствующих решениях
совпадают, т. е.
и, наоборот, любому допустимому
решению
расширенной задачи
соответствует допустимое решение
исходной задачи
.
При этом значения целевых функций
задач на соответствующих решениях
совпадают, т. е.
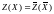 .
Док-во. Пусть
допустимое
решение. Тогда оно удовлетворяет:
.
Док-во. Пусть
допустимое
решение. Тогда оно удовлетворяет:
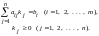 Дополним данное решение
Дополним данное решение
 ,
имеем
.
Подставим
,
имеем
.
Подставим
 в систему ограничений расширенной
задачи:
в систему ограничений расширенной
задачи:
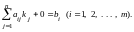 Данное
равенство выполняется, так как оно
не отличается от тождества.
является допустимым решением. Покажем,
что значения целевых функций задач
на соответствующих допустимых решениях
совпадают.
Данное
равенство выполняется, так как оно
не отличается от тождества.
является допустимым решением. Покажем,
что значения целевых функций задач
на соответствующих допустимых решениях
совпадают.
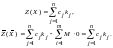 Отсюда
.
Отсюда
.
Лемма. Значение целевой функции
расширенной задачи на максимум
(минимум) на любом допустимом решении
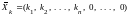 ,
у которого все искусственные переменные
равны нулю, больше
,
у которого все искусственные переменные
равны нулю, больше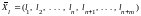 (меньше) значения целевой функции на
любом допустимом решении , у которого
хотя бы одна искусственная переменная
отлична от нуля. Док-во. Подставим
и
(меньше) значения целевой функции на
любом допустимом решении , у которого
хотя бы одна искусственная переменная
отлична от нуля. Док-во. Подставим
и
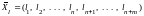 в целевую функцию расширенной задачи
в целевую функцию расширенной задачи
 ,
,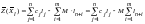 .
.
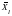 удовлетворяет условию неотрицательности
удовлетворяет условию неотрицательности
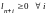 и по условию леммы
и по условию леммы
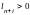 ,
то
,
то
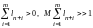 и
и
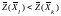 .
.
Т. Если расширенная задача линейного программирования имеет оптимальное решение
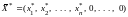 ,
у которого все искусственные переменные
равны нулю, то исходная задача имеет
оптимальное решение
,
у которого все искусственные переменные
равны нулю, то исходная задача имеет
оптимальное решение
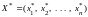 ,
которое получается из
,
которое получается из
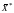 отбрасыванием этих нулевых искусственных
переменных. До-во. Пусть
отбрасыванием этих нулевых искусственных
переменных. До-во. Пусть
 .
Допустимому решению
соответствует допустимое решение
исходной задачи
,
что
.
Допустимому решению
соответствует допустимое решение
исходной задачи
,
что
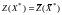 .
Покажем, что
оптимальное решение
исходной задачи, т.е.
.
Покажем, что
оптимальное решение
исходной задачи, т.е.
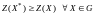 .
.
Пусть оптимальным решением исходной
задачи является
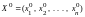 ,
т.е.
,
т.е.
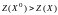
 ,
в частности
,
в частности
 .
Существует допустимое решение
расширенной задачи
.
Существует допустимое решение
расширенной задачи
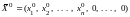 такое, что
такое, что
 .
Тогда
.
Тогда
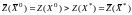 ,
что противоречит оптимальности
.
,
что противоречит оптимальности
.
2.) .Фундаментальная система решений однородной системы уравнений, теорема об её существовании. Векторная форма записи общего решения неоднородной системы уравнений.Фундаментальной системой решений однородной системы уравнений называется линейно независимая система векторов-решений системы F1, F2, … Fk, по которой разлагается любое решение системы, т.е. любое решение системы уравнений равно X=F1t1+F2t2+…+Fktk, где t1, t2, … tk – вещественные числа. Т. Если ранг матрицы системы однородных уравненийr меньше числа неизвестных n, то система уравнений имеет фундаментальную систему решений, состоящую из nr векторов-решений. Док: Пусть система записана в виде . Если ранг матрицы системы равен r(r(A)=r), то равносильная разрешенная система уравнений содержит r уравнений и имеет вид . Т. к.n>r, то система имеет n –rсвободных неизвестных . Задав свободным неизвестным значения 0 и 1, можно найти n –rчастных решений вида , , …, . В этих векторах вместо значений базисных переменных поставлены точки, так как они в данном рассмотрении не имеют значения. Покажем, что образуют фундаментальную систему решений. Чтобы доказать, что данные векторы являются линейно независимыми, составим линейную комбинацию .Данная линейная комбинация равна нулевому вектору только при . Это и подтверждает линейную независимость векторов. Покажем, что любое решение системы уравнений является линейной комбинацией . Составим вектор К, являющийся линейной комбинацией векторов с коэффициентами .Решения L и K при одних и тех же разрешенных неизвестных имеют одинаковые свободные неизвестные, следовательно, они совпадают (L= K), т. е. .
Векторная форма записи общего решения неоднородной сис-мы ур-ний. Т. Общее решение неоднородной системы уравнений АХ=В равняется сумме частного решения этой системы К и линейной комбинации решений фундаментальной системы решений соответствующей однородной системы АХ=0, т.е. Х=К+ F1t1+F2t2+…+Fktk, где К - какое-либо решение неоднородной системы уравнений АХ=В, F1, F2, … Fk – фундаментальная система решений однородной системы уравнений, t1, t2, … tk– произвольно заданные числа. Док-во: 1. Подставим X=К+F1t1+F2t2+…+Fktk в уравнение АХ=В, получим AX=A(К+F1t1+F2t2+…+Fktk)=AK+AF1t1+AF2t2+…+AFktk=B+©t2+…+©tk=B, так как векторы F1, F2, … Fk являются решениями однородной системы АХ=©. Значит, Х является решением системы АХ=В. 2.Покажем, что любое решение уравнения АХ=В имеет вид L= К+ F1t1+F2t2+…+Fktk. Пусть К – некоторое частное решение уравнения АХ=В, L – любое другое ршение этого уравнения. Разность эти решений (L-K) является решением одного уравнения AX=©. Действительно, A(L-K)=AL-AK=B-B=0. Поэтому L-K является линейной комбинацией векторов-решений фундаментальной системы однородной системы уравнений, т.е. L-K= F1t1+F2t2+…+Fktk.
Билет №10
1.) Обоснование метод искусственного
базиса решения задач линейного
программирования. Теорема об отсутствии
оптимального решения ввиду неограниченности
целевой функции. Метод
искусственного базиса применяется
в том случае если, задача не имеет
начального опорного решения с базисом
из единичных векторов. 1.Составляем
расширенную задачу. ( добавляем
искусственные переменные – не
отрицательные переменные которые
вводятся в левую часть одного из уравнений
системы ограничений с коэф. +1 и в целевую
функцию на макс. -М в задаче на минимум
+М). 2.Либо находим оптимальное решение,
либо устанавливаем его отсутствие.
Особенности1.Оценки
разложений векторов условий ∆j
= Сб
* Xj –
cj
состоят из двух слагаемых. Одно из
которых не зависит от М. На первом этапе
расчета, используем только слагаемые
оценок ∆J(M).
2.Векторы соответствующие иск. Переменным,
которые выводятся из базиса, исключаем
из рассмотрения. 3.Далее продолжаем
симплексным методом с использованием
оценок независящих от М. Т. Если
расширенная задача имеет оптимальное
решение, у которого хотя бы одна
искусственная переменная отлична от
нуля, то исходная задача не имеет
решения ввиду несовместности системы
ограничений. Док-во. Пусть
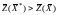
 ;
причем хотя бы одна из искусственных
переменных больше нуля. Покажем, что
система ограничений исходной задачи
в этом случае несовместна. Пусть есть
некоторое допустимое решение
;
причем хотя бы одна из искусственных
переменных больше нуля. Покажем, что
система ограничений исходной задачи
в этом случае несовместна. Пусть есть
некоторое допустимое решение
 ,
которому соответствует допустимое
решение расширенной задачи
и
.
,
которому соответствует допустимое
решение расширенной задачи
и
.
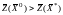 ,
что противоречит оптимальности
.
Т. Если расширенная задача не
имеет решения ввиду неограниченности
целевой функции, то и исходная задача
также не имеет решения по той же
причине. Док-во. Пусть
,
что противоречит оптимальности
.
Т. Если расширенная задача не
имеет решения ввиду неограниченности
целевой функции, то и исходная задача
также не имеет решения по той же
причине. Док-во. Пусть
 +.
Пусть есть оптимальное решение
,
которому соответствует допустимое
решение расширенной задачи
и
+.
Пусть есть оптимальное решение
,
которому соответствует допустимое
решение расширенной задачи
и
 .
Так как
.
Так как
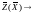 +,
то есть допустимое решение
+,
то есть допустимое решение
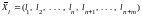 ,
что
,
что
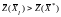 .
1)
.
1)
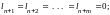 то
то
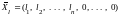 соответствует допустимое решение
исходной задачи
соответствует допустимое решение
исходной задачи
 и
,
и
,
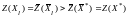 ,
что противоречит предположению об
оптимальности решения
,
что противоречит предположению об
оптимальности решения
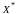 .
2) существует
.
2) существует
 ,
тогда
,
тогда
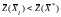 ,
что противоречит неограниченности
целевой функции (
+)
расширенной задачи
.
,
что противоречит неограниченности
целевой функции (
+)
расширенной задачи
.
2.) . Квадратичная форма: ее стандартный вид, изменение при невырожденном линейном преобразовании, канонический вид. Знакоопределенность квадратичных форм. Критерий Сильвестра. Квадратичной формой n переменных x1,x2,…,xn называется функция F(x1,x2,…,xn), представляющая собой сумму, каждое слагаемое которой имеет вторую степень относительно этих переменных. Обычно используют квадратичные формы следующего вида(cтандартная форма):
Матрица данного вида называется матрицей квадратичной формы.
.Матрица является симметрической, т.к. aij=aji i,j=1,2,…,n. Квадратичная форма в векторно-матричном виде: F(x)=XTAX, где . Преобразование квадратичной формы при невырожденном линейном преобразовании координат. X=CY, , , . Здесь x1 , x2 , …, xn – старые переменные, y1 , y2 , …, yn -новые переменные, С – матрица преобразования координат. Преобразование координат называется невырожденным, если матрица преобразования С невырожденная. Квадратичная форма F(x)=XTAX в новой системе координат примет вид F(Y)= (CY)TA(CY)=YTCTACY=YTA*Y, где A*=CTAC- матрица квадратичной формы в новой системе координат. Канонический вид квадратичной формы. Квадратичная форма называется канонической, если все ее коэффициенты aij при i ≠ j равны нулю, т.е. она имеет вид:
Матрица такой квадратичной формы является диагональной . Т. Любая квадратичная форма может быть приведена к каноническому виду с помощью невырожденного линейного преобразования. Знакоопределенность квадратичной формы. Канонический вид квадратичной формы определяется неоднозначно. Т. Число слагаемых с положительными (отрицательными) коэффициентами канонической квадратичной формы не зависит от способа приведения формы к этому виду. РАНГОМ квадратичной формы называется отличных от нуля коэффициентов в ее каноническом виде. Ранг квадратичной формы совпадает с рангом матрицы квадратичной формы. Квадратичная форма называется положительно (отрицательно) определенной, если она принимает положительные(отрицательные) значения в любой точке n-мерного пространства , кроме начала координат, т.е. . Т. Для того чтобы квадратичная форма F(Х)=XTAX была положительно(отрицательно) определенной, необходимо и достаточно, чтобы все собственные значения матрицы А были положительные(отрицательные). Критерий Сильвестра. Т. Для того чтобы квадратичная форма была положительно определенной, необходимо и достаточно, чтобы все главные миноры матрицы этой формы были положительны, т.е. , где (k=1,2,…,n)
Т. Если квадратичная форма удовлетворяет критерию Сильвестра, то она может быть приведена к каноническому виду
Билет № 11
1.) Пример составления двойственной задачи. Правило составления двойственной задачи. Симметричные и несимметричные пары двойственных задач. Имеется m-видов сырья b1,……bn, к-ые используются для производства n-видов продукции.Введём переменную aij-расход i-го сырья на изготовление единицы j-й продукции.Сj–прибыль от реализации единицы i-го вида продукции, Xj–объём выпуска j-й продукцииZ(x)=c1x1+c2x2+…+cnxn →max. Система: a11x1+a12x2+…+a1nxn≤b1, a21x1+a22x2+…+a2nxn≤b2, am1x1+am2x2+…+amnxn≤bmиxj≥0.
Предположим, что имеется 2-й производитель(2-я фирма) тоже производит какую-то продукцию и ей требуется то же сырьё, что и для 1-й. Рассматриваем задачу условий продажи сырья 1-й фирмы 2-й. Y=(y1,y2,…ym)-вектор цен единицы i-го вида сырья. F(Y)=b1y1 +b2y2+….+bmym →min. Система: a11y1+a21y2+…+am1ym≥c1, a12y1+a22y2+…+am2ym≥c2, a1ny1+a2ny2+…+amnym≥cn, yi≥0. Построили двойственную или сопряжённую исходной задачу.Правила составления двойственной задачи: 1)Во всех ограничениях основной задачи неизвестные стоят слева,а свободные переменные справа; 2)В ограничениях-неравенствах знаки должны быть направлены в одну сторонуМак--≤ , мин-- ≥; 4)Каждому ограничению исходной задачи соответствует переменная двойственной задачи,при этом ограничению нер-ву соответствует у>=0, а уравнению – не налагается усл неотрицат; 4) матрица системы ограничений двойтв.задачи-транспонированная матр системы огранич исходной; 5) коэффициенты целевой ф-ции дв задачи-правые части системы ограничений исходной, а правыми частями системы ограничений будут коэффициенты цел ф-ции исходной.
2.)
.N-мерные векторы
и действия над ними. Множество чисел
u1, u2,…,un,
пронумерованное с помощью натуральных
чисел и расставленных в порядке
возрастания их номеров, называется
числовой последовательностью.N-мерным
вектором называется последовательность
n чисел. Эти числа называют
координатами вектора. Число координат
вектора n называется
размерностью вектора. Запись вектора:
в виде строки или стоблца. .
Единичные векторы спец. вида -
.
Единичные векторы спец. вида -![]() нулевой вектор -
нулевой вектор -![]()
Скалярное
произведение векторов. Скалярным
произведением векторов ![]() и
и ![]() называется
величина, вычисляемая по формуле:
называется
величина, вычисляемая по формуле:

Модуль(длина
вектора)
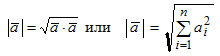 Если
модуль вектора равен 1 то он называется
единичным и обозначается через
Если
модуль вектора равен 1 то он называется
единичным и обозначается через![]() .
.
Угол между векторами
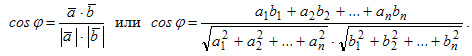
Матрицы. Линейные операции над матрицами. Матрицей размерности m на n называется таблица чисел(элементов), содержащих m строк и n столбцов.
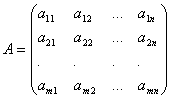 или А(aij)(i=1,2,…,m;j=1,2,...,
n). Если в матрице А
переставить соответствующие строки и
столбцы местами, то получится матрица
А^T, которую называют
транспонированной матрицей. Если число
m и n совпадают,
то матрицу называют квадратной n-порядка.
1)Матрицы
A = || ai j ||
и B = || ai j ||
считаются равными,
если они имеют одинаковые размеры и их
соответствующие матричные элементы
попарно равны:
или А(aij)(i=1,2,…,m;j=1,2,...,
n). Если в матрице А
переставить соответствующие строки и
столбцы местами, то получится матрица
А^T, которую называют
транспонированной матрицей. Если число
m и n совпадают,
то матрицу называют квадратной n-порядка.
1)Матрицы
A = || ai j ||
и B = || ai j ||
считаются равными,
если они имеют одинаковые размеры и их
соответствующие матричные элементы
попарно равны:![]() для
любых допустимых значений индексов i
и j.
2) Любую матрицу можно умножить на
любое число, при этом все элементы
матрицы умножаются на это число
для
любых допустимых значений индексов i
и j.
2) Любую матрицу можно умножить на
любое число, при этом все элементы
матрицы умножаются на это число
![]() 3) Операция сложения
определена только для матриц одинаковых
размеров. Результатом сложения матриц
A = || ai j ||
и B = || bi j ||
является матрица C = || ci j || ,
элементы которой равны сумме соответствующих
матричных элементов:
3) Операция сложения
определена только для матриц одинаковых
размеров. Результатом сложения матриц
A = || ai j ||
и B = || bi j ||
является матрица C = || ci j || ,
элементы которой равны сумме соответствующих
матричных элементов:![]() Умножение
матриц. Произведением двух матриц А
= (ai j) и B = (bj k), где i =
Умножение
матриц. Произведением двух матриц А
= (ai j) и B = (bj k), где i =![]() ,
j=
,
j=![]() ,
k=
,
k=![]() ,
заданных в определенном порядке АВ,
называется матрица С = (c i k),
элементы которой определяются по
следующему правилу: c ik =
ai
1 b1 k +
ai
2 b2 k +...
+ aim bmk =
,
заданных в определенном порядке АВ,
называется матрица С = (c i k),
элементы которой определяются по
следующему правилу: c ik =
ai
1 b1 k +
ai
2 b2 k +...
+ aim bmk = ![]() ais bsk.
Свойстваумноженияматриц:
1)(AB)C=A(BC); 2) (A+B)C= AC+AB; 3)
A(B+C)= AB+ AC; 4) AE=EA=A; 5)(AB)^T= (B^T)(A^T).
ais bsk.
Свойстваумноженияматриц:
1)(AB)C=A(BC); 2) (A+B)C= AC+AB; 3)
A(B+C)= AB+ AC; 4) AE=EA=A; 5)(AB)^T= (B^T)(A^T).
Билет №12
1.) Первая теорема
двойственности, её доказательство.Т.
Если одна из пары двойственных
задач имеет оптимальное решение, то
и двойственная к ней имеет оптимальное
решение; причем значения целевых
функций задач на своих оптимальных
решениях совпадают. Если же одна из
пары двойственных задач не имеет
решения ввиду неограниченности целевой
функции, то другая не имеет решения
ввиду несовместности системы
ограничений.Док-во. Есть несимметричная
пара двойственных задач. Первая:Z(X)
= CX max,
AX=
max,
AX=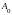 ,
,
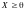 .
Вторая:
.
Вторая:
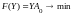 ,
,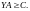 Оптимальное
решение первой задачи:
Оптимальное
решение первой задачи: с базисом
с базисом
 .
Запишем последнюю симплексную таблицу.
Запишем разложение вектора
:
.
Запишем последнюю симплексную таблицу.
Запишем разложение вектора
:
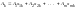 ,
k= 0, 1, 2, . . . , n.
Пусть
,
k= 0, 1, 2, . . . , n.
Пусть
 ,
k= 0, 1, 2, ..., n.
,
k= 0, 1, 2, ..., n.
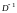
 D
D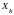 ,
=
.
Аналогично:
,
=
.
Аналогично:
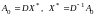 .
Напишем оценки
,
которые находятся по формуле:
.
Напишем оценки
,
которые находятся по формуле:
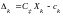 .
.
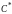 - матрица-строка коэффициентов при
базисных переменных. Тогда
- матрица-строка коэффициентов при
базисных переменных. Тогда
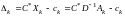 .
Пусть
.
Пусть ;
;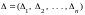 и
и ,
,
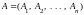 .
Значит,
.
Значит,
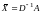 ,
, .
1. Допустимое решение двойственной
задачи:
.
1. Допустимое решение двойственной
задачи:
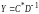 .Решение
прямой задачи
.Решение
прямой задачи
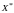 на мак:
на мак:
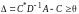 ,
,
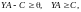 удовлетворяет системе ограничений
двойственной задачи. 2. Докажем
удовлетворяет системе ограничений
двойственной задачи. 2. Докажем
 и
и
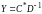 .
.
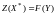 ,
,
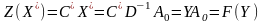 .
3. Докажем
.
3. Докажем
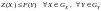 ,
,
 область
допустимых решений прямой задачи,
область
допустимых решений прямой задачи,
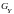
область допустимых решений двойственной
задачи.
область допустимых решений двойственной
задачи.
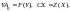
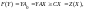 т.е.
т.е.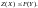 4.
Докажем, что
4.
Докажем, что
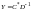 является оптимальным решением.
оптимальное решение, то
является оптимальным решением.
оптимальное решение, то
 .
Двойственная задача на мин, то должно
выполняться
.
Двойственная задача на мин, то должно
выполняться
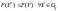 .
.
 ,
,
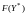 не может быть меньше
не может быть меньше
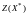 ,
а может быть только равно
.
Это равенство достигается при
,
а может быть только равно
.
Это равенство достигается при
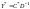 ,которое
- оптимальным решением двойственной
задачи.
,которое
- оптимальным решением двойственной
задачи.
Докажем второе утверждение. Пусть
прямая задача не имеет оптимального
решения, так как Z(X)
+.
Так как
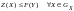 и
и
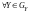 ,
то
,
то
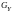 -
пустое множество.
-
пустое множество.
2.)
Понятие о линейном алгебраическом
уравнении, его решении. В общем случае
линейное ур-ние имеет вид:
![]() .
Любой n-мерный вектор Х =
(x 1, x 2, ..., x n ),
называется решением уравнения, если
при подстановке его координат уравнение
обращается в тождество. 2 линейных ур-ния
называются равносильными, если они
имеют одно и то же множество решений.
Решение линейного ур-ния: 1)
a1=a2=…=an=b=0,
тогда ур-ние 0x 1+ 0x 2+
...+0x n =0-тривиальное ур-ние, имеет
бесконечное мн-во реш; 2) a1=a2=…=an,
b не равен 0, тогда 0x 1+
0x 2+ ...+0x n =b-противоречивое
ур-ние, не имеет ни 1 решения; 3) хотя бы
один из коэфф.при неизвестных отличен
от 0.пусть а не равно0, тогда можно
разрешить ур-ние относительно х1;
.
Любой n-мерный вектор Х =
(x 1, x 2, ..., x n ),
называется решением уравнения, если
при подстановке его координат уравнение
обращается в тождество. 2 линейных ур-ния
называются равносильными, если они
имеют одно и то же множество решений.
Решение линейного ур-ния: 1)
a1=a2=…=an=b=0,
тогда ур-ние 0x 1+ 0x 2+
...+0x n =0-тривиальное ур-ние, имеет
бесконечное мн-во реш; 2) a1=a2=…=an,
b не равен 0, тогда 0x 1+
0x 2+ ...+0x n =b-противоречивое
ур-ние, не имеет ни 1 решения; 3) хотя бы
один из коэфф.при неизвестных отличен
от 0.пусть а не равно0, тогда можно
разрешить ур-ние относительно х1;
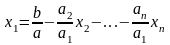 ,
х1-разрешенная неизвестная, х2,х3…-
свободные неизвестные. Системы линейных
ур-ний, их классификация по количеству
решений. В общем случае система лин.
ур-ний, имеет вид
,
х1-разрешенная неизвестная, х2,х3…-
свободные неизвестные. Системы линейных
ур-ний, их классификация по количеству
решений. В общем случае система лин.
ур-ний, имеет вид
,
где a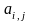 (i=1,2…,m;j=1,2,…,n)
и
(i=1,2…,m;j=1,2,…,n)
и (i=1,2,…m)-постоян.
велич. Решением системы ур-ний называется
такой n-мерный вектор Х =
(x 1, x 2, ..., x n ),
который является решением каждого из
уравнений системы. 1) 2 системы называются
равносильными, если они имеют одно
и то же множество решений. 2) Система
ур-ний называется совместной, если
она имеет хотя бы 1 решение. 3) Система
ур-ний называется несовместной,
если она не имеет ни 1 решения. 4)Совместная
система называется определенной,
если она имеет единственное решение.
5) Совсестная система называется
неопределенной, если она имеет
бесконечное мн-во решений. Векторная
и матричная формы записи систем линейных
уравнений. Система ур-ний может быть
записана в векторном виде:
(i=1,2,…m)-постоян.
велич. Решением системы ур-ний называется
такой n-мерный вектор Х =
(x 1, x 2, ..., x n ),
который является решением каждого из
уравнений системы. 1) 2 системы называются
равносильными, если они имеют одно
и то же множество решений. 2) Система
ур-ний называется совместной, если
она имеет хотя бы 1 решение. 3) Система
ур-ний называется несовместной,
если она не имеет ни 1 решения. 4)Совместная
система называется определенной,
если она имеет единственное решение.
5) Совсестная система называется
неопределенной, если она имеет
бесконечное мн-во решений. Векторная
и матричная формы записи систем линейных
уравнений. Система ур-ний может быть
записана в векторном виде:
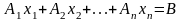 ,
где
,
где
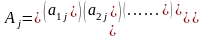 ,
j=1,2,…,n; B=
,
j=1,2,…,n; B=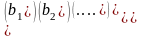 В матричной записи система линейных
ур-ний может быть записана: AX=B,
где A=
В матричной записи система линейных
ур-ний может быть записана: AX=B,
где A= ,
X=
,
X=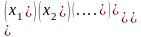 ,
B=
.
,
B=
.
Билет №13
1.) Вторая теорема двойственности, её
доказательство.Т. Для того, чтобы
допустимые решения
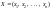 ,
,
 являлись оптимальными решениями пары
двойственных задач, необходимо и
достаточно, чтобы выполнялись следующие
равенства
являлись оптимальными решениями пары
двойственных задач, необходимо и
достаточно, чтобы выполнялись следующие
равенства ;
;
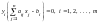 .
Док-во. Необходимость.
.
Док-во. Необходимость.
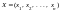 и
и
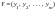
оптимальные решения пары двойственных
задач. 1.
оптимальные решения пары двойственных
задач. 1.
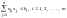 ;
; .
.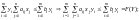
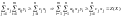 .Отсюда
следует
.Отсюда
следует .X,
Y
оптимальные решения, то Z(X)
= F(Y).
.X,
Y
оптимальные решения, то Z(X)
= F(Y).
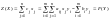 .
.
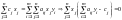 .Учитывая,
что
.Учитывая,
что
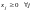 и
и
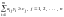 ,
а
,
а
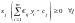 ,
из этого каждое слагаемое суммы равно
нулю, т.е.
,
из этого каждое слагаемое суммы равно
нулю, т.е.
 .2.
Аналогично:
.2.
Аналогично: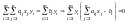 .
Так как
.
Так как
 и
и
 ,
,
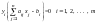 .Достаточность.
.Достаточность.
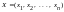 и
и
 являются оптимальными решениями.
являются оптимальными решениями.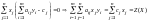 ;
;
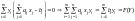 .
Получаем, что Z(X)
= F(Y).
Из первой теоремы двойственности
следует, что значения целевых функций
пары двойственных задач равны только
на оптимальных решениях. Поэтому
можно утверждать, что X
и Y являются
оптимальными решениями.
.
Получаем, что Z(X)
= F(Y).
Из первой теоремы двойственности
следует, что значения целевых функций
пары двойственных задач равны только
на оптимальных решениях. Поэтому
можно утверждать, что X
и Y являются
оптимальными решениями.
2.)
Разрешенная система уравнений. Общее,
частное и базисное решение. Неизвестная
 называется разрешенной для системы
ур-ний, если она входит в 1 из ур-ний
системы с коэфф.+1, а в остальные уравнения
не входит (т.е. входит с коэфф.=0). Система
ур-ний называется разрешенной, если
каждое ур-ние системы содержит разрешенную
неизвестную, среди которых нет совпадающих.
Разрешенные неизв., взятые по одному из
каждого ур-ния, образуют полный набор
разреш.неизвестных. Разрешенные неизв,
входящие в набор-базисные, а не
входящие-свободные. Общим решением
разрешенной системы называется
совокупность выражений разрешенных
неизвестных через свободные члены и
свободные неизвестные. Частным решением
системы ур-ний называется решение,
получающееся из общего при конкретных
значениях свободных неизвестных.
Базисным решение системы ур-ний
наз. частное решение, получающееся из
общего при нулевых знач. Базисное
реш.-вырожденное, если число
координат,отличных от нуля < числа
разреш.неизвестных. Базисное
реш.-невырожденное, если
координат,отличных от нуля =числу
разреш.неизвестных. Т. Разрешенная
система всегда совместна, причем если
система не имеет свободных неизвестных,
то она определена, если же имеется хотя
бы одна своб.неизв, то система не
определена. Для любой системы ур-ний
общим решением называется общее реш.
разрешенной сист.,равносильной этой.
Если разрешенная система ур-ний,
равносильная исходной системе, содержит
n неизвестных и m
ур-ний (m<n),
то число общих и соотв.базисных реш.равно:
называется разрешенной для системы
ур-ний, если она входит в 1 из ур-ний
системы с коэфф.+1, а в остальные уравнения
не входит (т.е. входит с коэфф.=0). Система
ур-ний называется разрешенной, если
каждое ур-ние системы содержит разрешенную
неизвестную, среди которых нет совпадающих.
Разрешенные неизв., взятые по одному из
каждого ур-ния, образуют полный набор
разреш.неизвестных. Разрешенные неизв,
входящие в набор-базисные, а не
входящие-свободные. Общим решением
разрешенной системы называется
совокупность выражений разрешенных
неизвестных через свободные члены и
свободные неизвестные. Частным решением
системы ур-ний называется решение,
получающееся из общего при конкретных
значениях свободных неизвестных.
Базисным решение системы ур-ний
наз. частное решение, получающееся из
общего при нулевых знач. Базисное
реш.-вырожденное, если число
координат,отличных от нуля < числа
разреш.неизвестных. Базисное
реш.-невырожденное, если
координат,отличных от нуля =числу
разреш.неизвестных. Т. Разрешенная
система всегда совместна, причем если
система не имеет свободных неизвестных,
то она определена, если же имеется хотя
бы одна своб.неизв, то система не
определена. Для любой системы ур-ний
общим решением называется общее реш.
разрешенной сист.,равносильной этой.
Если разрешенная система ур-ний,
равносильная исходной системе, содержит
n неизвестных и m
ур-ний (m<n),
то число общих и соотв.базисных реш.равно:
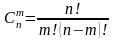
Эквивалентные преобразования систем линейных ур-ний . Системы линейных ур-ний приводятся к равносильным разрешенным системам с помощью элементарных преобразований. Т. Если какое либо ур-ние системы умножить на нек., отличное то 0 число, а остальные оставить без изменения, то получится система , равносильная данной. Док-во: Пусть 2 системы отличаются только одним ур-нием с номером i, причем это ур-ние 2 системы получено из соотв. ур-ния 1 системы умножением на λ, не равное 0
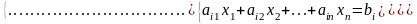 ,
,
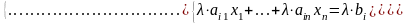 , если
, если
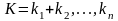 )-
решение одной из систем, то все совпадающие
ур-ния систем удовлетворяются этим
решением , а i-е ур-ния
обращаются в тождество одновременно.
Т. Если к какому то ур-нию системы
прибавить другое, а все остальные ур-ния
оставить без изменения, то получится
система, равносильная данной.Док-во:
Пусть исходная система имеет вид:
)-
решение одной из систем, то все совпадающие
ур-ния систем удовлетворяются этим
решением , а i-е ур-ния
обращаются в тождество одновременно.
Т. Если к какому то ур-нию системы
прибавить другое, а все остальные ур-ния
оставить без изменения, то получится
система, равносильная данной.Док-во:
Пусть исходная система имеет вид:
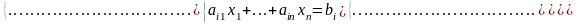 (1)
(1)
 (2)
(2)
Ур-ние с номером l прибавим к ур-нию с i .Получим (2) -решение исходной системы, то (1) и (2)- тождества, т.е. явл. Решением системы, полученной при сложении ур-ний с i и l. Следствие. Если к какому-либо ур-нию прибавить другое, умноженное на некоторое число, а все остальные оставить без изменения, то получится система, равносильная данной
Билет №14
1.)
2.)
Преобразование Жордана систем линейных
ур-ний. Вывод формул пересчета коэффициентов
системы уравнений.Преобразование
Жордана состоит из элементарных
преобразований:1) уравнение с разрешающим
элементом
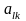 делится на этот элемент(умножается на
1/
);
2) ур-ние с разреш. элементом умножается
на подходящие множители и прибавляется
ко всем другим ур-ниям для того, чтобы
исключить неизвестную
делится на этот элемент(умножается на
1/
);
2) ур-ние с разреш. элементом умножается
на подходящие множители и прибавляется
ко всем другим ур-ниям для того, чтобы
исключить неизвестную
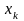 из
этих уравнений. Запишем 2 ур-ния: ур-ние
с номером l, содержащие
разрешающий элемент
и другое, с номером i
из
этих уравнений. Запишем 2 ур-ния: ур-ние
с номером l, содержащие
разрешающий элемент
и другое, с номером i
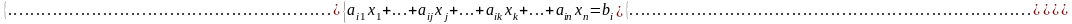 ,
*
,
*
 .
При делении ур-ние с номером l
на
,
его коэфф. пересчитываются по формулам:
.
При делении ур-ние с номером l
на
,
его коэфф. пересчитываются по формулам: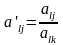 (j=1,2,…,n),
(j=1,2,…,n),
 .
Чтобы исключить
из ур-ния с i, нужно ур-ние
с номером l умножать на
и
прибавить к этому ур-нию.При этом, коэфф.
ур-ния с номером i
пересчитываются по формулам
.
Чтобы исключить
из ур-ния с i, нужно ур-ние
с номером l умножать на
и
прибавить к этому ур-нию.При этом, коэфф.
ур-ния с номером i
пересчитываются по формулам
 (i=1,2,...,m, i≠l; j=1,2,…,n);
(i=1,2,...,m, i≠l; j=1,2,…,n);
 (i=1,2,…, m; i≠l)
(i=1,2,…, m; i≠l)
Билет №15
1.) Необходимые и
достаточные условия разрешимости
транспортной задачи. Свойство системы
ограничений транспортной задачи.
Взаимосвязь линейной зависимости
векторов-условий и циклов.Т. Для
того, чтобы транспортная задача линейного
программирования имела решение,
необходимо и достаточно, чтобы суммарные
запасы поставщиков равнялись суммарным
запросам потребителей, т. е. задача
должна быть с правильным балансом.
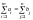 ,
,
Док-во. Необходимость.
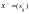 ,
,
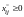 ,
i = 1, 2, ..., m;
j = 1, 2, ..., n.
Допустимое решение. Докажем
,
i = 1, 2, ..., m;
j = 1, 2, ..., n.
Допустимое решение. Докажем
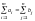 .
.
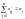 ,
i = 1, 2, ..., m,
,
i = 1, 2, ..., m,
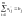 ,
j = 1, 2, ..., n
.
,
j = 1, 2, ..., n
.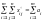 и
и
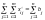 .
.
Отсюда следует, что задача имеет
правильный баланс.Достаточность.
Пусть задача имеет правильный баланс
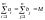 .
Докажем, что в этом случае задача
имеет оптимальное решение.
.
Докажем, что в этом случае задача
имеет оптимальное решение.
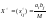 ,
i = 1, 2, ..., m;
j = 1, 2, .., n
- допустимое решение.
,
i = 1, 2, ..., m;
j = 1, 2, .., n
- допустимое решение.
 ,
i = 1, 2, ..., m,
,
i = 1, 2, ..., m,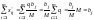 ,
j = 1, 2, ..., n,
,
j = 1, 2, ..., n, удовлетворяет и условиям неотрицательности.
удовлетворяет и условиям неотрицательности.
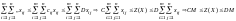 .
.
Свойство
системы ограничений транспортной
задачи. Взаимосвязь линейной зависимости
векторов-условий и циклов.Т.
Ранг системы векторов-условий транспортной
задачи равен
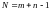 .Док-во.Для
нахождения базиса системы векторов
.Док-во.Для
нахождения базиса системы векторов
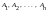 необходимо составить однородную систему
уравнений
необходимо составить однородную систему
уравнений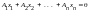 .Ранг
системы векторов равен числу векторов,
входящих в базис, т. е. числу разрешённых
неизвестных этой системы.Системе
векторов условий транспортной задачи
.Ранг
системы векторов равен числу векторов,
входящих в базис, т. е. числу разрешённых
неизвестных этой системы.Системе
векторов условий транспортной задачи
 ,
i=1,
2, ..., m;
j
= 1, 2, ...,
nсоответствует
однородная система уравнений
,
i=1,
2, ..., m;
j
= 1, 2, ...,
nсоответствует
однородная система уравнений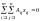 .
Записываем матрицу
этой системы. Если к последней строке
прибавить (n–1)
строку, начиная с (m+
1)-й, и вычесть первые m
строк, то получится строка, состоящая
из нулей. Это значит, число разрешенных
неизвестных и r
не может быть равен числу m+
n.Покажем,
что найдутся N
= m+
n
1 линейно независимых векторов условий.
Выбираем
.
Записываем матрицу
этой системы. Если к последней строке
прибавить (n–1)
строку, начиная с (m+
1)-й, и вычесть первые m
строк, то получится строка, состоящая
из нулей. Это значит, число разрешенных
неизвестных и r
не может быть равен числу m+
n.Покажем,
что найдутся N
= m+
n
1 линейно независимых векторов условий.
Выбираем
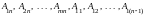 и убедимся, что они линейно независимые.
Система уравнений составляется:
и убедимся, что они линейно независимые.
Система уравнений составляется:
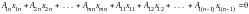 .C
помощью элементарных преобразований
можно привести ее к единичной.
Следовательно, эта система уравнений
имеет единственное нулевое решение
.C
помощью элементарных преобразований
можно привести ее к единичной.
Следовательно, эта система уравнений
имеет единственное нулевое решение
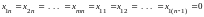 ,
а система векторов линейно независима.Т.Для
того чтобы система векторов-условий
транспортной задачи была линейно
зависимой, необходимо и достаточно,
чтобы из соответствующих им клеток
таблицы можно было выделить часть,
которая образует цикл.Док-во.
Необходимость.
,
а система векторов линейно независима.Т.Для
того чтобы система векторов-условий
транспортной задачи была линейно
зависимой, необходимо и достаточно,
чтобы из соответствующих им клеток
таблицы можно было выделить часть,
которая образует цикл.Док-во.
Необходимость.
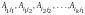 линейно
зависима. Тогда существует такой
ненулевой набор чисел
линейно
зависима. Тогда существует такой
ненулевой набор чисел
 ,
что
,
что
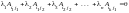 .
.
 .
Вектор
.
Вектор
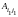 имеет
две равные единице координаты с номерами
имеет
две равные единице координаты с номерами
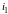 и
и
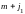 ,
остальные =0. В равенство входит вектор
,
остальные =0. В равенство входит вектор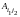 ,
у которого одна из этих координат =1
и который должен умножаться на
коэффициент
,
у которого одна из этих координат =1
и который должен умножаться на
коэффициент
 .
Но он имеет координату с номером
.
Но он имеет координату с номером
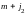 =ую 1. Следовательно, в равенство должен
также входить вектор с такой же
единичной координатой и т.д. В выбранной
таким образом последовательности
векторов должен найтись вектор
=ую 1. Следовательно, в равенство должен
также входить вектор с такой же
единичной координатой и т.д. В выбранной
таким образом последовательности
векторов должен найтись вектор
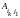 ,
у которого второй индекс совпадает
со вторым индексом первого вектора.
Данной последовательности векторов
соответствует совокупность клеток
таблицы транспортной задачи, которая
образует цикл.Достаточность.
Пусть из соответствующих векторам
,
у которого второй индекс совпадает
со вторым индексом первого вектора.
Данной последовательности векторов
соответствует совокупность клеток
таблицы транспортной задачи, которая
образует цикл.Достаточность.
Пусть из соответствующих векторам
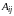 клеток (i,
j)
выбрана последовательность клеток,
образующих цикл (
клеток (i,
j)
выбрана последовательность клеток,
образующих цикл (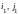 ),
(
),
(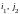 ),
(
),
(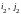 ),
…, (
),
…, ( ).
Нетрудно видеть, что
).
Нетрудно видеть, что
 .
Отсюда следует линейная зависимость
рассматриваемой системы векторов.
.
Отсюда следует линейная зависимость
рассматриваемой системы векторов.
2.) Метод Жордана-Гаусса решения систем линейных уравнений.Для того, чтобы составить алгоритм решения систем уравнений методом Ж.Г., необходимо использовать:Т.(О сокращении числа уравнений системы.) Если система уравнений содержит тривиальное ур-ние, то его можно исключить из системы, при этом получится система, равносильная исходной.Т. (О несовместности системы уравнений.) Если система ур-ний содержит противоречивое ур-ние, то она несовместна.Алгоритм метода Жордана-Гаусса:1) Проверяется, является ли система несовместной. Если система содержит противоречивое уравнение, то она несовместна; 2) Проверяется возможность сокращения числа ур-ний. Если система содержит тривиальное ур-ние, то его вычеркивают; 3) если система ур-ний является разрешенной, то записывают общее решение, если необходимо-частные; 4) Если система не является разрешенной, то в ур-нии, не содержащем разрешенной неизвестной, выбирают разрешающий элемент и производят преобразование Жордана с этим элементом.Далее переходят к пункту1. Теорема о разрешении однородной системы ур-ний. (Система ур-ний называется однородной, если правые части(свободные члены) всех ур-ний равны нулю). Если число неизвестных однородной системы n больше числа ур-ний m, то система имеет хотя бы одно ненулевое решение.Решение называется нулевым, если все его координаты равны нулю. Док-во. Т.к. правые части системы равны нулю, то она имеет нулевое решение Х=(0,0,…,0), т.е. она совместна. Если эту систему привести к равносильной разрешенной, то она будет иметь хотя бы одну свободную переменную , т.к. число ур-ний m меньше числа неизвестных n. Свободными неизвестным можно придать ненулевые значения и получить частное ненулевое решение.
Билет№ 16
1.) Метод северо-западного угла. Существует ряд методов построения начального опорного решения, наиболее простой - метод северо-западного угла, в котором запасы очередного по номеру поставщика используются для обеспечения запросов очередных по номеру потребителей до тех пор, пока не будут исчерпаны полностью, после чего используются запасы следующего по номеру поставщика. Заполнение таблицы транспортной задачи начинается с левого верхнего угла. Метод состоит из ряда однотипных шагов, которые определяются: 1) если ai< b j то х ij = аi, и исключается поставщик с номером i, т.е. принимается xik = 0, k = 1, 2, ..., n , k ≠j, а запросы j-го потребителя уменьшаются на ai , т.е. bj’=bj - ai 2) если ai> b j то х ij = bj, и исключается потребитель с номером j, xkj= 0, k= 1,2, ..., m, k≠i, а запасы i-го поставщика уменьшаются ai‘= ai - bj, 3) если a i = bj то хij= ai= bj, исключается либо поставщик с номером i, xik= 0, k= 1,2, ..., n, k≠j, , bj’=0 , либо j-й потребитель, xkj= 0, k= 1,2, ..., m, k≠i, ai‘= 0.
Нулевые
перевозки принято заносить в таблицу
только тогда, когда они попадают в
клетку (i, j),
подлежащую заполнению. Во избежание
ошибок после построения начального
опорного решения необходимо проверить,
что число занятых клеток равно k+ n-
1 и
векторы-условия, соответствующие этим
клеткам линейно независимы. Метод
минимальной стоимости. Метод
минимальной стоимости позволяет
построить опорное решение, достаточно
близкое к оптимальному, так как использует
матрицу стоимостей транспортной
задачи C={cij}, i=1,2,
..., m, j=1,2,
..., n.
Состоит из ряда однотипных шагов, на
каждом из которых заполняется только
одна клетка таблицы, соответствующая
минимальной стоимости min
{с ij}},
и исключается из рассмотрения только
одна строка (поставщик) или один столбец
(потребитель). Очередную клетку,
соответствующую min
{с ij},
заполняют по тем же правилам, что и в
методе северо-западного угла. Метод
вычеркивания. Позволяет
проверить, является ли данное решение
транспортной задачи опорным.Пусть
допустимое решение транспортной задачи,
которое имеет m+n-1 отличных от нуля
координат, записано в таблицу. Чтобы
данное решение было опорным, векторы-условий,
соответствующие положительным
координатам, а также базисным нулям,
должны быть линейно независимыми. Для
этого клетки должны быть расположены
так, чтобы нельзя было из них образовать
цикл.Следовательно, чтобы вычеркнуть
сначало либо все строки таблицы,
содержащие по одной занятой клетке,
либо все столбцы, содержащие по одной
занятой клетке, далее вернуться к
столбцам (строкам) и продолжать
вычеркивание. Переход
от одного опорного решения к другому.
В
транспортной задаче переход от одного
опорного решения к другому осуществляется
с помощью цикла. Для некоторой свободной
клетки таблицы строится цикл, содержащий
часть клеток, занятых опорным решением.
По этому циклу перераспределяются
объемы перевозок. Перевозка загружается
в выбранную свободную клетку и
освобождается одна из занятых клеток,
получается новое опорное решение. Т.
Если таблица транспортной задачи
содержит опорное решение, то для любой
свободной клетки таблицы существует
единственный цикл, содержащий эту клетку
и часть клеток, занятых опорным
решением. Означенный
цикл.
Цикл
называется означенным, если его угловые
клетки пронумерованы по порядку и
нечетным клеткам приписан знак «+», а
четным — знак «-». Сдвигом по циклу
на величину θ называется
увеличение объемов перевозок во всех
нечетных клетках цикла, отмеченных
знаком «+», на θ и
уменьшение объемов перевозок во всех
четных клетках, отмеченных знаком «-»,
на θ. Т.
Если таблица транспортной задачи
содержит опорное решение, то при сдвиге
по любому циклу, содержащему одну
свободную клетку, на величину ![]() получится
опорное решение.
получится
опорное решение.
Т. Если таблица транспортной задачи содержит опорное решение, то для любой свободной клетки таблицы существует единственный цикл, содержащий эту клетку и часть клеток, занятых опорным решением.
2.)
Определение линейно зависимой и
линейно независимой систем векторов,
их свойства. Линейная зависимость
векторов. Выражение вида ƛ1А1+ƛ2А2+…+ƛnAn
– линейная комбинация векторов
А1,А2,…,Аn
c коэффициентами ƛ1,
ƛ2,…, ƛn. В=
ƛ1А1+ƛ2А2+…+ƛnAn
. Система векторов А1,А2,…,Аn
называется линейно зависимой, если
существует ненулевой набор чисел ƛ1,
ƛ2,…, ƛn, при
котором линейная комбинация векторов
ƛ1А1+ƛ2А2+…+ ƛnAn
равняется нулевому вектору Θ, т.е.
система уравнений А1х1+А2х2+…+Аnxn=
Θ имеет ненулевое решение. Система
векторов А1,А2,…,Аn
называется линейно независимой,
если линейная комбинация этих векторов
ƛ1А1+ƛ2А2+…+ƛnAn
равна нулевому вектору только при
нулевом наборе чисел ƛ1, ƛ2,…,
ƛn, т.е. система
уравнений А1х1+А2х2+…+Аnxn=
Θ имеет единственное нулевое решение.
Св-во 1. Если система векторов линейно
зависимая, то хотя бы один из векторов
разлагается по остальным и, наоборот,
если хотя бы один из векторов системы
разлагается по остальным, то система
векторов линейно зависимая. Док-во.
Если система векторов А1,А2,…,Аn
линейно зависимая, то существует
ненулевой набор ƛ1, ƛ2,…, ƛn,
при котором линейная комбинация этих
векторов равняется нулевому вектору,
т.е. ƛ1, ƛ2,…, ƛn
= Θ. Пусть ƛ1 ≠0, тогда
 .
А1 разлагается по остальным
векторам. 2. ƛ1А1+ƛ2А2+…+ƛnAn
, -1∙А1+ ƛ2А2+…+ƛnAn=
Θ. А1х1+А2х2+…+Аnxn=
Θ имеет ненулевое решение (-1, ƛ1,
ƛ2,…, ƛn.).
Система векторов – линейно зависимая.
Св-во 2. Если какая – либо подсистема
векторов линейно зависимая, то и вся
система линейно зависимая. Док-во.
А1,А2,…,Аr
линейно зависимая подсистема А1,А2,…,Аn
(r<n).
Тогда есть ƛ1, ƛ2,…, ƛn,
такой, что ƛ1А1+ƛ2А2+
…+ƛrAr=
Θ. ƛ1, ƛ2,…, ƛr,0,...,0
ненулевой набор, при котором ƛ1А1+ƛ2А2+
…+ƛrAr+0Аr+1+…+0An
= Θ, т.е. система А1,А2,…,Аn
линейно зависимая. Св-во 3. Если
система векторов линейно независимая,
то любая ее подсистема линейно независимая.
Док-во. Если подсистема векторов линейно
зависимая, тогда по предыдущему свойству
вся система векторов линейно зависимая,
что противоречит условию. Св-во 4. Любая
система векторов, содержащая нулевой
вектор, линейно зависимая. Док-во.
ƛ1А1+ƛ2А2+
…+ƛrAn+Аn+1
Θ для любых векторов А1,А2,…,Аn
и нулевого вектора Θ равняется
нулевому вектору при ненулевом наборе
ƛ (0,0,…,0,1), так как 0∙А1+0∙А2+…+0∙Аn+
ƛn+1 Θ= Θ. Св-во
5. Система m-мерных
векторов всегда является линейно
зависимой, если число векторов n
больше их размерности (n>m).
Док-во. Составим однородную систему
уравнений А1х1+А2х2+…+Аnxn=
Θ. При n>m
существует ненулевой набор чисел
х1,х2,…,хn,
при котором линейная комбинация
векторов равна нулевому вектору.
.
А1 разлагается по остальным
векторам. 2. ƛ1А1+ƛ2А2+…+ƛnAn
, -1∙А1+ ƛ2А2+…+ƛnAn=
Θ. А1х1+А2х2+…+Аnxn=
Θ имеет ненулевое решение (-1, ƛ1,
ƛ2,…, ƛn.).
Система векторов – линейно зависимая.
Св-во 2. Если какая – либо подсистема
векторов линейно зависимая, то и вся
система линейно зависимая. Док-во.
А1,А2,…,Аr
линейно зависимая подсистема А1,А2,…,Аn
(r<n).
Тогда есть ƛ1, ƛ2,…, ƛn,
такой, что ƛ1А1+ƛ2А2+
…+ƛrAr=
Θ. ƛ1, ƛ2,…, ƛr,0,...,0
ненулевой набор, при котором ƛ1А1+ƛ2А2+
…+ƛrAr+0Аr+1+…+0An
= Θ, т.е. система А1,А2,…,Аn
линейно зависимая. Св-во 3. Если
система векторов линейно независимая,
то любая ее подсистема линейно независимая.
Док-во. Если подсистема векторов линейно
зависимая, тогда по предыдущему свойству
вся система векторов линейно зависимая,
что противоречит условию. Св-во 4. Любая
система векторов, содержащая нулевой
вектор, линейно зависимая. Док-во.
ƛ1А1+ƛ2А2+
…+ƛrAn+Аn+1
Θ для любых векторов А1,А2,…,Аn
и нулевого вектора Θ равняется
нулевому вектору при ненулевом наборе
ƛ (0,0,…,0,1), так как 0∙А1+0∙А2+…+0∙Аn+
ƛn+1 Θ= Θ. Св-во
5. Система m-мерных
векторов всегда является линейно
зависимой, если число векторов n
больше их размерности (n>m).
Док-во. Составим однородную систему
уравнений А1х1+А2х2+…+Аnxn=
Θ. При n>m
существует ненулевой набор чисел
х1,х2,…,хn,
при котором линейная комбинация
векторов равна нулевому вектору.
Билет №17
1.)
Признак
оптимальности опорного решения в методе
потенциалов. Этот
метод позволяет упростить наиболее
трудоемкую часть вычислений – нахождение
оценок свободных клеток. Т.
Если допустимое решение Х=(![]() ),
i=1,2,,…,m,
j=1,2,…,n
транспортной задачи является оптимальным,
то существует потенциалы (числа)
поставщиков
),
i=1,2,,…,m,
j=1,2,…,n
транспортной задачи является оптимальным,
то существует потенциалы (числа)
поставщиков
![]() ,
i=1,2,,…,m
и потребителей
,
i=1,2,,…,m
и потребителей
![]() ,
j=1,2,…,n,
удовлетворяющие следующим условиям:
+
=
,
j=1,2,…,n,
удовлетворяющие следующим условиям:
+
=![]() при
>0,
+
при
>0,
+
![]() при
=0.
Признак
оптимальности: опорное решение является
оптимальным, если для всех векторов-условий
(клеток таблицы) оценки неположительные.
при
=0.
Признак
оптимальности: опорное решение является
оптимальным, если для всех векторов-условий
(клеток таблицы) оценки неположительные.
2.) Базис
системы векторов. Единственность
разложения вектора по базису. Теорема
об единичном базисе. Базисом системы
векторов А1,А2,…,Аn
называется такая ее подсистема
В1,В2,…,Вn,
которая линейно независимая и по которой
разлагается любой вектор системы. Здесь
r-число векторов, входящих
в базис (r≤n).
Т. об единственности разложения
векторов по базису. Любой вектор
системы разлагается по базису этой
системы единственным образом. Док-во.
Пусть есть разложения вектора Аj
системы А1,А2, …, Аn
по базису В1,В2,…,Вr.
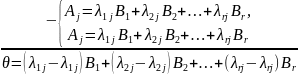 .
Так как В1, В2,…, Вn,
образующие базис, линейно независимые,
то последнее равенство возможно только
при нулевом наборе множителей при
векторах, т.е. только при ƛ1j=ƛ’1j,
ƛ2j=ƛ’2j,…,
ƛrj=ƛ’rj.
Т. об единичном базисе системы векторов.
Если система m - мерных
векторов содержит m
различных единичных векторов Е1,Е2,…,Еm
, то они образуют базис этой системы.
Единичным вектором называется вектор,
модуль которого равен единице. Док- во.
Пусть система имеет вид А1,А2,…,Аn,
Е1,Е2,…,Еm.
1. Е1,Е2,…,Еm
– линейно независимые, так как
система Е1х1+Е2х2+…+Emxm=
Θ имеет единственное нулевое решение.
.
Так как В1, В2,…, Вn,
образующие базис, линейно независимые,
то последнее равенство возможно только
при нулевом наборе множителей при
векторах, т.е. только при ƛ1j=ƛ’1j,
ƛ2j=ƛ’2j,…,
ƛrj=ƛ’rj.
Т. об единичном базисе системы векторов.
Если система m - мерных
векторов содержит m
различных единичных векторов Е1,Е2,…,Еm
, то они образуют базис этой системы.
Единичным вектором называется вектор,
модуль которого равен единице. Док- во.
Пусть система имеет вид А1,А2,…,Аn,
Е1,Е2,…,Еm.
1. Е1,Е2,…,Еm
– линейно независимые, так как
система Е1х1+Е2х2+…+Emxm=
Θ имеет единственное нулевое решение.

2. Покажем, что любой m – мерный вектор Аj разлагается по этой системе единичных векторов.
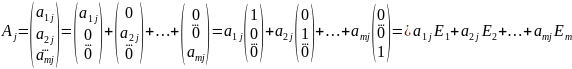
Следовательно, координаты любого m – мерного вектора Аj являются коэффициентами разложения его по базису из единичных векторов Е1,Е2,…,Еm.
Билет №18
1.)
Особенности
решения транспортной задачи с неправильным
балансом. 1.
Пусть суммарные запасы поставщиков
превосходят суммарные запросы
потребителей, т.е.
![]() .
В этом случае при составлении оптимального
плана перевозок часть запасов поставщиков,
равная
.
В этом случае при составлении оптимального
плана перевозок часть запасов поставщиков,
равная
![]() =
=![]() ,
останется не вывезенной. Поэтому первую
группу уравнений следует заменить
неравенствами
,
останется не вывезенной. Поэтому первую
группу уравнений следует заменить
неравенствами
![]() ,
i=1,2,…,m,
а вторая группа без изменений. Для
приведения к канонической форме вводят
дополнительные переменные
,
i=1,2,…,m,
а вторая группа без изменений. Для
приведения к канонической форме вводят
дополнительные переменные
![]() .
.
![]() ,
i=1,2,…,m.
Математическая модель задачи принимает
вид
,
i=1,2,…,m.
Математическая модель задачи принимает
вид
![]()
![]()
![]() ,
,
,
i=1,2,…,m
,
![]() ,
j=1,
2, … , n,
,
j=1,
2, … , n,
![]() ,
i=1,2,,…,m,
j=1,2,…,n+1.
,
i=1,2,,…,m,
j=1,2,…,n+1.
Необходимое
и достаточное условие:
![]() ,
,
![]()
![]() .
2. Аналогично когда суммарные запросы
потребителей превосходят суммарные
запасы поставщиков, т.е.
.
2. Аналогично когда суммарные запросы
потребителей превосходят суммарные
запасы поставщиков, т.е.
![]() ,
часть запросов потребителей, равная
,
часть запросов потребителей, равная
![]() =
=![]() ,
останется не удовлетворенной. Вторая
группа уравнений:
,
останется не удовлетворенной. Вторая
группа уравнений:
![]() ,
j=1,
2, … , n.
,
j=1,
2, … , n.
Математическая
модель:
![]() ,
,
![]() ,
i=1,2,…,m
,
,
i=1,2,…,m
,
![]() ,
j=1,
2, … , n,
,
i=1,2,,…,m+1,
j=1,2,…,n.
Необходимое и достаточное:
,
j=1,
2, … , n,
,
i=1,2,,…,m+1,
j=1,2,…,n.
Необходимое и достаточное:
![]() ,
,
![]()
![]() .
.
2.) Теорема о двух линейно независимых системах векторов. Теорема о числе векторов, входящих в базис. Ранг системы векторов. Т. Если система линейно независимых векторов, содержащая n векторов, разлагается по другой линейно независимой системе векторов, содержащей m векторов, то n≤m. Док-во. Пусть есть линейно независимые системы векторов А1,А2, …, Аn и В1,В2,…,Вm, и векторы первой системы разлагаются по векторам второй системы. Предположим, что n>m.
. Существует ƛ1, ƛ2,…, ƛn, при котором А1 ƛ1+А2 ƛ2+…+ Anƛn. Равняется нулевому вектору Θ. . Должна иметь ненулевое решение. Эта система имеет ненулевое решение ƛ1, ƛ2,…, ƛn, так как по предположению число неизвестных n больше числа m. Это противоречит тому, что система векторов А1,А2, …, Аn является линейно зависимой. Предположение n>m неверно. Следовательно, n≤m. Т о числе векторов, входящих в базис. Любой базис системы векторов содержит одно и то же число векторов. Число векторов, входящих в базис системы векторов, называется рангом системы векторов. Док-во. Пусть система векторов А1,А2, …, Аn имеет два базиса. Базис Б1=( В1,В2,…,Вm) содержит m векторов, а базис Б2=(C1, C2,...,Ck) содержит k векторов. Каждый из базисов представляет собой независимую систему векторов и векторы каждого базиса разлагаются по векторам другого базиса. Поэтому по теореме о линейно независимых векторах m≤k и k≤m.
Билет №19
1.) Транспортная задача с ограничениями. Пусть требуется при решении транспортной задачи ограничить перевозки от поставщика с номером l к потребителю с номером k. Ограничения двух типов: I ) xlk > а ; 2) xlk<b , а и b - постоянные величины. 1. xlk > a , то необходимо прежде, чем решать задачу, сократить (уменьшить) запасы l-го поставщика и запросы m-го потребителя на величину а (зарезервировать перевозку xlk = а ). После решения задачи в оптимальном решении следует увеличить объем перевозки xlk на величину а. 2. xlk <b , то необходимо вместо k -го потребителя с запросами bk ввести двух других потребителей. Один из них с номером m должен иметь запросы b 'k=b, а другой с номером п + 1- запросы bп+1= bk - b. Стоимости перевозок для этих потребителей остаются прежними, за исключением стоимости cl(n+1) которая принимается равной сколь угодно большому числу М (М >> 1). После получения оптимального решения величины грузов, перевозимых к (n + 1)-му потребителю, прибавляются к величинам перевозок l-го потребителя. Так как cl(n+1)) = М -самая большая стоимость перевозки, то в оптимальном решении клет ка с номером (l, n+ 1) останется пустой, xl{n+1) = 0 и объем перевозки хlk не превзойдет b .
2.) Теорема о двух системах векторов, которым соответствуют равносильные системы уравнений. Алгоритм нахождения базиса. Т.Если двум системам векторов А1,А2, …, Аn и В1,В2,…,Вn соответствуют равносильные системы уравнений А1х1+А2х2+…+Аnxn= Θ, B1х1+В2х2+…+Вnxn= Θ, и векторы В1,В2,…,Вr образуют базис системы, то соответствующие векторы А1, А2,…,Аr образуют базис системы и при этом разложения соответствующих векторов систем по своим базисам совпадают, т.е. Вj=B1 ƛ1j+B2 ƛ2j+…+Br ƛrj (j=r+1, 2,…, n), то Aj=A1 ƛ1j+A2 ƛ2j+…+Ar ƛrj (j=r+1, 2,…,n). Док-во. Пусть В1,В2,…,Вr (r≤n) базис системы векторов (2). Покажем, что А1, А2,…,Аr линейно зависимы, т.е. есть ненулевой набор ƛ1, ƛ2, …, ƛr,что А1 ƛ1+А2 ƛ2+…+ Ar ƛr= Θ. А1 ƛ1+А2 ƛ2+…+ Ar ƛr+ Ar+10+ Ar+20+…+ An0= Θ. B1 ƛ1+B2 ƛ2+…+Br ƛr+Br+10+Br+20+…+Bn0= Θ или B1 ƛ1+B2 ƛ2+…+Br ƛr= Θ при ненулевом наборе чисел ƛ1, ƛ2, …, ƛr, что возможно только при линейной зависимости векторов В1,В2,…,Вr. Это противоречит условию теоремы. Следовательно, А1, А2,…,Аr линейно независимые. Вj=B1 ƛ1j+B2 ƛ2j+…+Br ƛrj (j=1, 2,…, n). Покажем, что с такими же коэффициентами ƛ1j, ƛ2j,…, ƛrj разлагается Aj по векторам А1, А2,…,Аr . B1 ƛ1+B2 ƛ2+…+Br ƛr+Br+10+Br+20+…+Bj-10-Bj∙1+Bj+10+…+ Bn0= Θ A1 ƛ1+A2 ƛ2+…+Ar ƛr+Ar+10+Ar+20+…+Aj-10-Aj∙1+Aj+10+…+ An0= Θ, Aj= ƛ1+A2 ƛ2+…+Ar ƛr (j=1, 2,…, n). Алгоритм нахождения базиса. 1) составить соответствующую системе векторов однородную систему уравнений А1х1+А2х2+…+Аnxn= Θ; 2)привести эту систему к равносильной разрешенной системе вида E1x1+E2x2+…+Erxr+A’r+1xr+1+…+A’jxj+…+A’nxn= Θ; 3) записать базис системы векторов Б=(А1, А2,…,Аr); 4) записать разложения векторов по базису; коэффициентами разложения вектора Aj по этому базису являются координаты соответствующего вектора A’j= (a’1j, a’2j,…,a’rj) в разрешенной системе уравнений, т.е. A’j=А1 a’1j, А2 a’2j,…, Аr a’rj (j=1, 2, …, n). Система векторов, состоящая из n векторов, ранг которой равен r, может иметь несколько базисов. Число возможных базисов системы векторов определяется как число сочетаний из n по r по формуле
Билет №20
1.) Использование транспортной задачи для решения других экономических задач.
Транспортная
задача по критерию времени. Задача
о размещении производства с учетом
транспортных затрат .Имеется m пунктов
производства с объемами
производства ![]() и n пунктов
потребления с объемами потребления
и n пунктов
потребления с объемами потребления ![]() .
Затраты на производство единицы продукции
в каждом i-м
пункте равны
.
Затраты на производство единицы продукции
в каждом i-м
пункте равны ![]() , i=1,2,…,m.
Стоимости перевозки единицы груза от
каждого i–го
производителя каждому j–му
потребителю известны и равны
, i=1,2,…,m.
Стоимости перевозки единицы груза от
каждого i–го
производителя каждому j–му
потребителю известны и равны ![]() . Суммарные объемы производства
превосходят суммарные объемы потребления.
Задача решается как транспортная задача,
матрица стоимостей которой составляется
как сумма матриц:
С=(
. Суммарные объемы производства
превосходят суммарные объемы потребления.
Задача решается как транспортная задача,
матрица стоимостей которой составляется
как сумма матриц:
С=(![]() )=(
+
), i=1,2,,…,m, j=1,2,…,n. Вводится
фиктивный потребитель. Затем задача
решается обычным способом. Задача
о назначениях, или проблема выбора.
Имеется m групп
людей численностью
,
которые должны выполнять n видов
работ объемом
.
Известна производительность каждой i–й
группы людей при выполнении каждого j–го
вида работ, i=1,2,,…,m, j=1,2,…,n. .
Математическая модель по аналогии с
транспортной задачей
)=(
+
), i=1,2,,…,m, j=1,2,…,n. Вводится
фиктивный потребитель. Затем задача
решается обычным способом. Задача
о назначениях, или проблема выбора.
Имеется m групп
людей численностью
,
которые должны выполнять n видов
работ объемом
.
Известна производительность каждой i–й
группы людей при выполнении каждого j–го
вида работ, i=1,2,,…,m, j=1,2,…,n. .
Математическая модель по аналогии с
транспортной задачей![]()
![]()
![]() ,
, ![]() , i=1,2,…,m ,
, i=1,2,…,m , ![]() , j=1,
2….n,
, j=1,
2….n, ![]() , i=1,2,,…,m, j=1,2,…,n.
, i=1,2,,…,m, j=1,2,…,n.
Целевая функция: - . Транспортная задача по критерию времени. Возникает при перевозке срочных грузов. Имеется m поставщиков с запасами однородного груза в количестве и n потребителей . Известно , i=1,2,,...,m, j=1,2,...,n - время, за которое груз доставляется от каждого i-го поставщика каждому j-му потребителю. Математическая модель: хij - объем перевозимого груза от i-го поставщика j-му потребителю. Х=(хij) i=1,2,,...,m, j=1,2,...,n - некоторое опорное решение задачи. Обозначим через Т(Х) наибольшее значение элементов матрицы Т=(tij), i=1,2,,...,m, j=1,2,...,n, соответствующих клеткам таблицы, занятым опорным решением: Т(Х)=max{tij}. Математическая модель имеет вид: Т(Х)= max{tij} min, , i=1,2,...,m , j=1, 2, ... , n, хij >=0, i=1,2,,...,m+1, j=1,2,...,n. Находится начальное опорное решение Х1. определяется значение целевой функции Т(Х1)= max{tij}= tl1k1. Все свободные клетки со значением tik >T(X1), исключаются из рассмотрения. Чтобы понизить значение целевой ф-ции, необходимо освободить клетку (l, k), для которой tij достигает максимума. Для этого строят разгрузочные циклы, которые могут включать в свой состав несколько свободных клеток. В каждом разгрузочном цикле, начиная с разгружаемой клетки (l, k), расставляются поочередно знаки "-" и "+" и осуществляется сдвиг на величину . Если удается эту клетку разгрузить, то она исключается из рассмотрения (зачеркивается). Получается новое опорное решение Х2, на котором значение целевой функции меньше, чем на Х1.
2.) Базис как максимальная линейно независимая подсистема векторов. Пусть в системе векторов А1, А2, …, Аn имеется хотя бы один отличный от нулевого вектор и этим вектором является А1. Будем искать другой вектор системы, который линейно независим с вектором А1. Пусть таким вектором является А2. Векторы А1 и А2 образуют подсистему линейно независимых векторов. Продолжим увеличивать число векторов в подсистеме так, что бы они оставались линейно независимыми. Пусть А1, А2, …, Аr линейно независимые, а присоединение любого другого вектора системы Аj приводит к линейно зависимой подсистеме. Тогда векторы А1, А2, …, Аrобразуют базис системы А1, А2, …, Аn (они удовлетворяют условию базиса: 1. Они линейно независимые; 2. Любой вектор системы можно разложить по ним.) Покажем, что вектор Аj разлагается по векторам А1, А2, …, Аr. А1, А2, …, Аr, Аj– линейно независимые, то есть ненулевой набор чисел b1, b2, …, br, bj, что A1b1+A2b2 +…+Arbr+Ajbj=©. bj не равно 0, но если это так, то какое0либо из чисел отлично от нуля, то A1b1+A2b2 +…+Arbr=© при ненулевом наборе чисел, что противоречит линейной независимости векторов А1, А2, …, Аr. Поэтому базис называют максимально линейно независимой подсистемой вектором. Т. Если ранг системы векторов равен r, то любая подсистема из r линейно независимых векторов является базисом системы векторов. (Так как ранг = r, то любая подсистема из r является максимально линейно независимой подсистемой и базисом системы векторов.) N-мерное векторное пространство. Множеством всех n-мерных векторов, рассматриваемое в совокупности с линейными операциями сложения и умножения на число, называется n-мерным векторным пространством Rn. Базисом Rn может служить полный набор из n различных единичных векторов E1, E2, …, En или любая другая подсистема из n линейно независимых векторов.
