Министерство экономики РФ Министерство образовния РФ

ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ  ВЫСШАЯ ШКОЛА ЭКОНОМИКИ

Методические указания по курсу "Линейная алгебра"

для Экономического Направления

Составитель: д.ф.-м.н., профессор Гусятников П.Б.

****************************************************************************************

Домашняя работа №1 ( Решение типового варианта , 1 неделя).

1. А) Для пары матриц вычислите те из матриц

AB, BA, A*B, BA*, AB*, B*A, A*B*, B*A*, A+B, B+A, A*+B, B+A*, A+B*, B*+A, A*+B*, B*+A*, которые определены ( ^*  символ транспонирования матриц).

б) Проделайте те же операции для пары матриц и

в) для пары матриц .

г) Выясните, какие из следующих матричных тождеств верны, а какие – нет (одно из верных тождеств докажите): A+C=C+A; AC=CA; (AC)*=A*C*; (AC)*=C*A*; (A+C)*=C*+A*.

Решение.

а) Произведение двух матриц определено тогда и только тогда, когда длина строки первого сомножителя равна высоте второго.

Размеры матриц:

( длина строки  2, высота столбца  3);

( длина строки  3, высота столбца  2);

( длина строки  3, высота столбца  2);

( длина строки  2, высота столбца  3).

Следовательно, определены следующие произведения и только они: AB, BA, A*B*, B*A*.

Вычислим эти произведения.

Поскольку . Исходя из этого факта, сделаем разметку

для матрицы :

(произведение имеет три строки и три столбца). Заполним ячейки этой матрицы. Покажем, как вычислить, например, элемент матрицы, расположенный во второй строке и третьем столбце:

Методические указания стр.2

***************************************************************************************

.

Аналогично заполняются остальные ячейки матрицы :

.

Из того факта, что , следует, что произведение определено и имеет размеры 2x2 :

Исходя из этого, сделаем разметку и проведем расчеты для матрицы :

(произведение имеет две строки и два столбца).

Легко видеть, что (даже размеры этих матриц различны!!!). Вывод:

умножение матриц в общем случае некоммутативно.

Далее, . Следовательно, произведение определено и .

Подробно:

(произведение имеет две строки и два столбца).

Легко видеть, что 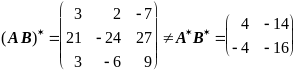(размеры этих матриц различны!!!).

Однако бросается в глаза, что . Этот факт справедлив не только для данных матриц, но и для любых двух матриц, для которых произведение определено.

ТЕОРЕМА. Если , то :

после транспонирования

порядок сомножителей меняется на противоположный!

Именно, имеет место

Приведем доказательство этой теоремы.

Отметим прежде всего, что для строки и столбца

Методические указания стр.3

***************************************************************************************

. (1)

Далее, заметим, что из включений следует, что

,

в связи с чем произведение определено и имеет те же размеры, что и матрица .

При этом в соответствии с равенством (1), учитывая, что при транспонировании матриц строки становятся столбцами: , а столбцы  строками: , имеем

:

.

Равенство подчеркнутых выражений при всех и означает равенство матриц

. Теорема доказана.

В нашем примере осталось вычислить произведение . Этого уже можно не делать, поскольку, как доказано выше, .

Займемся сложением матриц. Сумма двух матриц определена тогда и только тогда, когда когда оба слагаемых имеют одинаковые размеры. У нас

; ; ; .

Поэтому определены лишь следующие суммы (сложение двух матриц одинаковых размеров происходит покомпонентно!):

;

.

Внимательный студент заметит, что полученные в этих двух цепочках вычислений ответы связаны соотношением . Это совпадение не является случайным (мы приводим здесь решение п.г))

ТЕОРЕМА.. Если , то .

Методические указания стр.4

*************************************************************************************

Доказательство. В каждом из этих равенств матрицы, стоящие в левой и правой частях, имеют одинаковые размеры. Остается убедиться в совпадении соответствующих компонент матриц.

Действительно, для всех i=1,...,m; j=1,...,n имеем

 (сумма двух действительных чисел не зависит от порядка слагаемых!)=

Доказательство завершено.

б) ,

Поэтому определены лишь следующие матрицы ( ни одна из интересующих нас сумм не определена!)

.

в) Для пары матриц имеем

.

Поэтому определены следующие матрицы

;

;

;

;

.

Методические указания стр.5

*************************************************************************************

2. Найдите матрицу Х из уравнения уравнения 7A - 2X - 5B = , где

, ,   нулевая матрица размеров 3x4.

Решение. Искомая матрица X имеет имеет размеры 3x4. По правилам действий над матрицами (сложение, вычитание матриц и умножение матриц на число происходят покомпонентно!)

.

3. Решите матричные уравнения (x и y – неизвестные действительные числа) и дайте геометрическую интерпретацию системы получившихся обычных уравнений:

а) ;

б) .

Решение. a) По определению действий со столбцами уравнение равносильно системе уравнений (сложение

Оба уравнения решенной выше системы суть уравнения прямых на координатной плоскости Oxy, а найденные нами числа суть координаты точки пересечения M(6;5) этих прямых.

б) Аналогично, уравнение

равносильно системе уравнений

Методические указания стр.6

*************************************************************************************

Дискриминант D квадратного уравнения равен . Поэтому корни этого квадратного уравнения суть

.

Таким образом, рассматриваемая система уравнений имеет два решения:

и .

Дадим геометрическую интерпретацию решенной системы уравнений и полученных реше-ний. Уравнение в прямоугольной декартовой системе координат Oxy есть уравнение окружности C с центром в точке и радиусом .

Второе уравнение в рассмотренной системе есть уравнение прямой L. Решив систему уравнений, мы, таким образом, нашли точки пересечения и прямой L с окруж-ностью C .