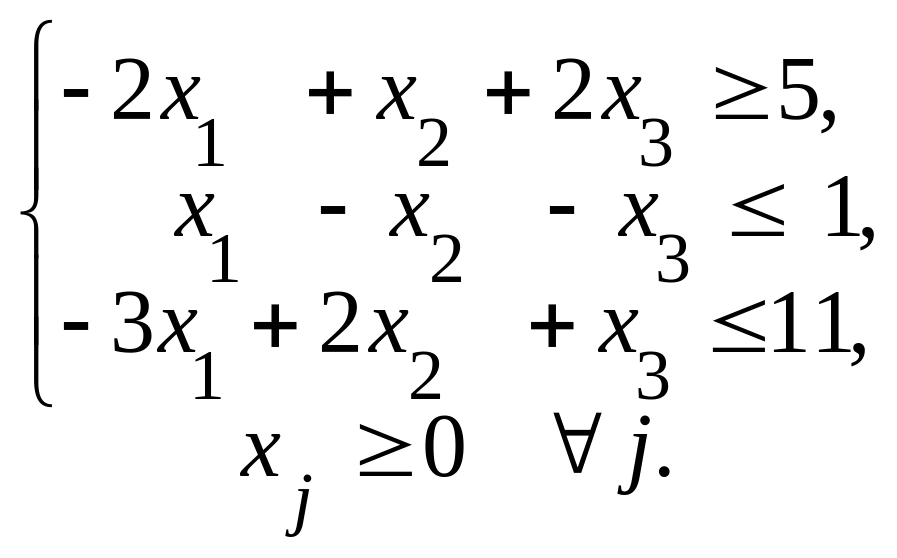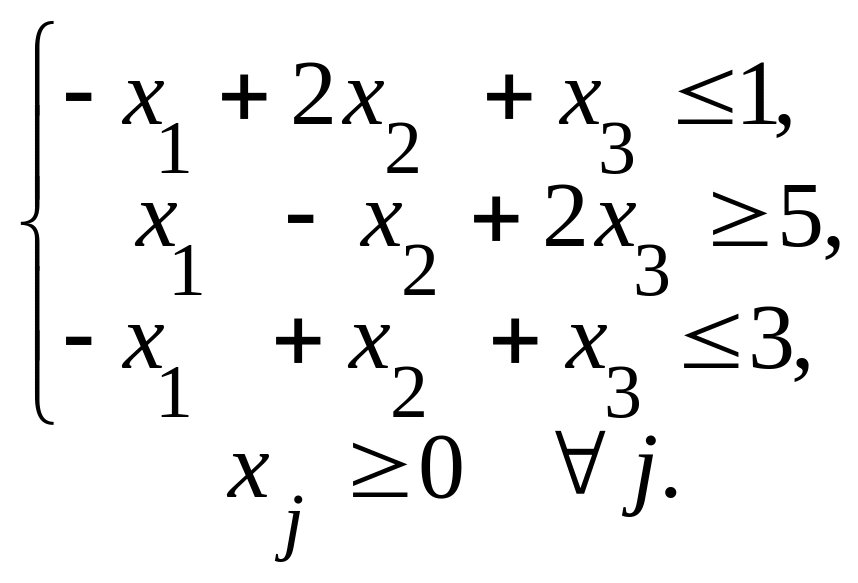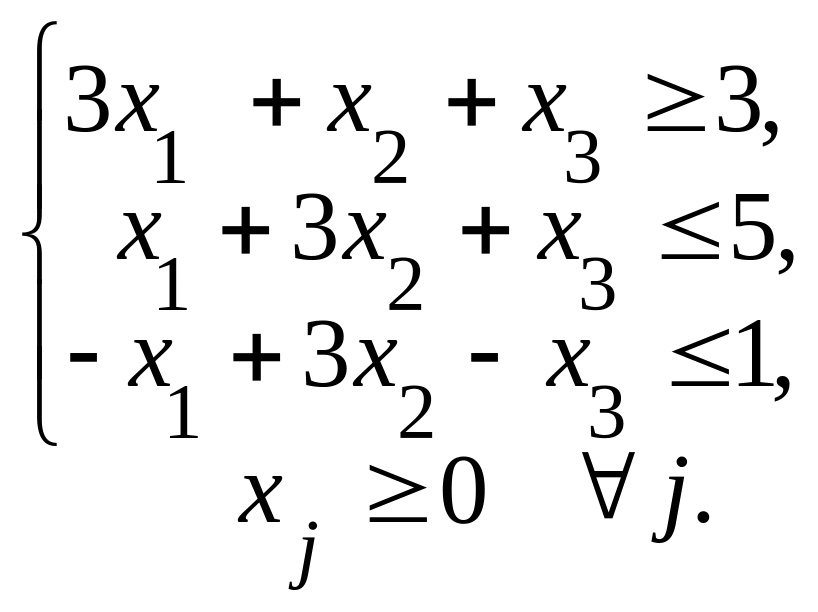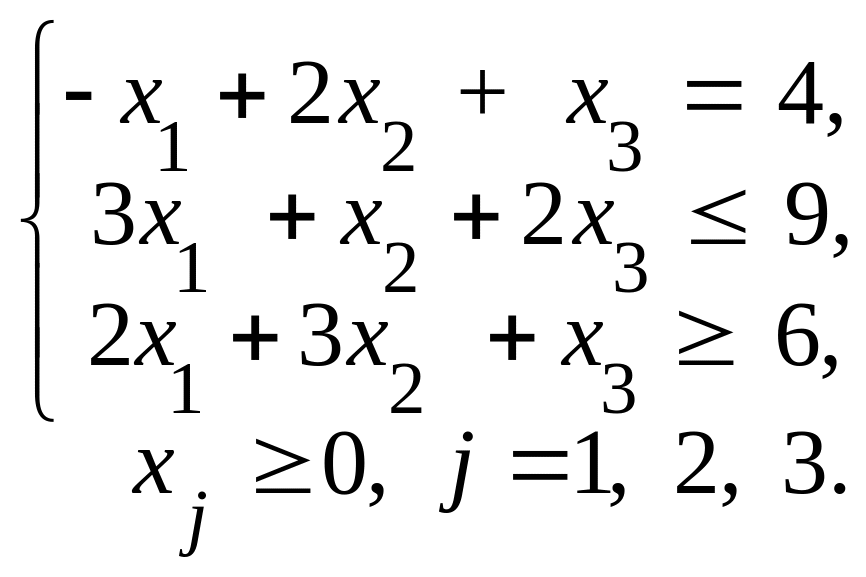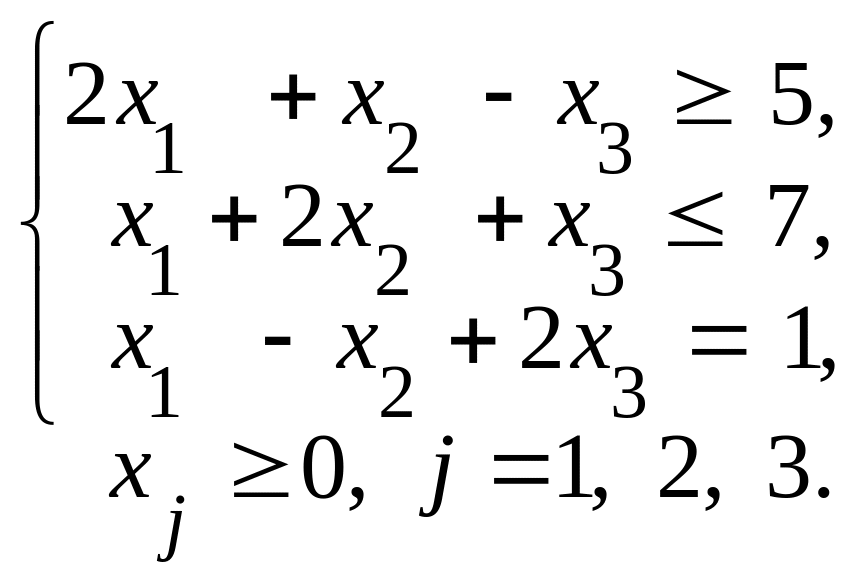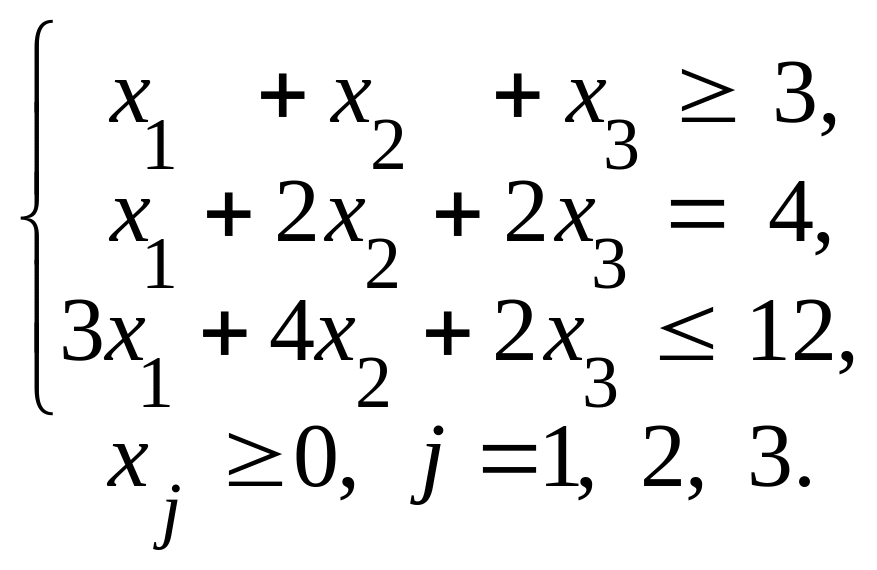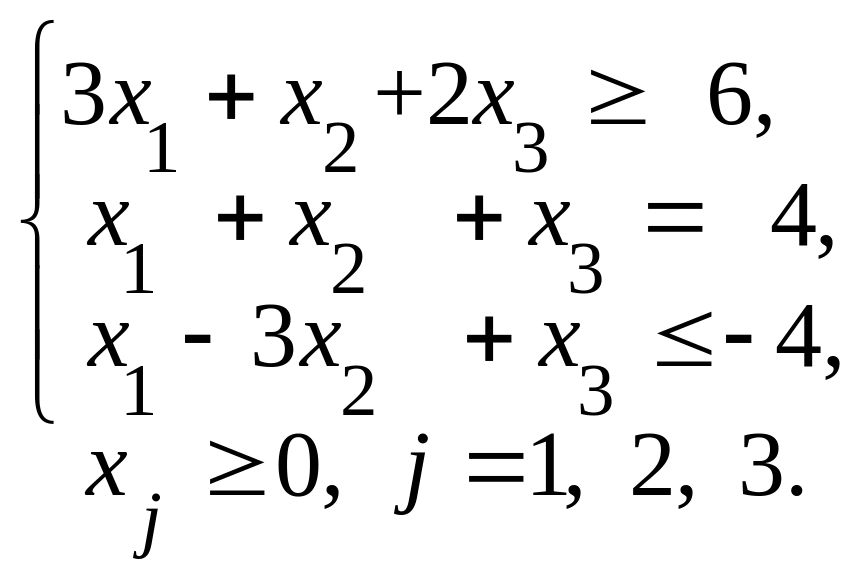- •Билет № 1
- •2. Теорема о решении однородной системы линейных уравнений.
- •Билет № 2
- •2. Необходимые и достаточные условия разрешимости транспортной задачи линейного программирования.
- •Билет № 3
- •2. Базис системы векторов. Теорема о единственности разложения вектора по базису.
- •Билет № 4
- •2. Теорема об улучшении опорного решения задачи линейного программирования, её следствия (признак оптимальности опорного решения).
- •Билет № 5
- •2. Теорема об оптимальности опорного решения задачи линейного программирования с искусственными переменными.
- •Билет № 6
- •2. Теоремы об отсутствии оптимального решения задачи линейного программирования с искусственными переменными.
- •Билет № 7
- •2. Теорема об экстремуме целевой функции задачи линейного программирования.
- •Билет № 8
- •2. Первая теорема двойственности.
- •Билет № 9
- •2. Вторая теорема двойственности.
- •Билет № 10
- •2. Построение начального опорного решения задачи линейного программирования и переход от одного опорного решения к другому.
- •Ответы к задачам
Федеральное агентство по образованию ГОУ ВПО «Российский экономический университет им. Г.В.Плеханова» Кафедра Высшей математики Специальность 080100 «Финансы и кредит» Дисциплина Линейная алгебра Билет № 1 1. Составить математическую модель задачи линейного программирования об использовании ресурсов (производственной задачи). 2. Теорема о решении однородной системы линейных уравнений.
|
Федеральное агентство по образованию ГОУ ВПО «Российский экономический университет им. Г.В.Плеханова» Кафедра Высшей математики Специальность 080100 «Финансы и кредит» Дисциплина Линейная алгебра Билет № 2 1. Линейно зависимые и линейно независимые системы векторов, их свойства. 2. Необходимые и достаточные условия разрешимости транспортной задачи линейного программирования.
|
Федеральное агентство по образованию ГОУ ВПО «Российский экономический университет им. Г.В.Плеханова» Кафедра Высшей математики Специальность 080100 «Финансы и кредит» Дисциплина Линейная алгебра Билет № 3 1. Транспортная задача линейного программирования. Текстовая формулировка. Математическая модель. 2. Базис системы векторов. Теорема о единственности разложения вектора по базису.
|
Федеральное агентство по образованию ГОУ ВПО «Российский экономический университет им. Г.В.Плеханова» Кафедра Высшей математики Специальность 080100 «Финансы и кредит» Дисциплина Линейная алгебра Билет № 4 1. Матрицы. Линейные операции над ними. Умножение матриц. 2. Теорема об улучшении опорного решения задачи линейного программирования, её следствия (признак оптимальности опорного решения).
|
Федеральное агентство по образованию ГОУ ВПО «Российский экономический университет им. Г.В.Плеханова» Кафедра Высшей математики Специальность 080100 «Финансы и кредит» Дисциплина Линейная алгебра Билет № 5 1. Графический метод решения задачи линейного программирования 2. Теорема об оптимальности опорного решения задачи линейного программирования с искусственными переменными.
|
Федеральное агентство по образованию ГОУ ВПО «Российский экономический университет им. Г.В.Плеханова» Кафедра Высшей математики Специальность 080100 «Финансы и кредит» Дисциплина Линейная алгебра Билет № 6 1. Опорное решение транспортной задачи линейного программирования, методы его построения. 2. Теоремы об отсутствии оптимального решения задачи линейного программирования с искусственными переменными.
|
Федеральное агентство по образованию ГОУ ВПО «Российский экономический университет им. Г.В.Плеханова» Кафедра Высшей математики Специальность 080100 «Финансы и кредит» Дисциплина Линейная алгебра Билет № 7 1. Приведение общей задачи линейного программирования к каноническому виду. 2. Теорема об экстремуме целевой функции задачи линейного программирования.
|
Федеральное агентство по образованию ГОУ ВПО «Российский экономический университет им. Г.В.Плеханова» Кафедра Высшей математики Специальность 080100 «Финансы и кредит» Дисциплина Линейная алгебра Билет № 8 1. Признак оптимальности опорного решения в методе потенциалов решения транспортной задачи линейного программирования. 2. Первая теорема двойственности.
|
Федеральное агентство по образованию ГОУ ВПО «Российский экономический университет им. Г.В.Плеханова» Кафедра Высшей математики Специальность 080100 «Финансы и кредит» Дисциплина Линейная алгебра Билет № 9 1. Обратная матрица. 2. Вторая теорема двойственности.
|
Федеральное агентство по образованию ГОУ ВПО «Российский экономический университет им. Г.В.Плеханова» Кафедра Высшей математики Специальность 080100 «Финансы и кредит» Дисциплина Линейная алгебра Билет № 10 1. Двойственные задачи линейного программирования, правило их составления. 2. Построение начального опорного решения задачи линейного программирования и переход от одного опорного решения к другому.
|
Билет № 1
2. Теорема о решении однородной системы линейных уравнений.
Теорема 2.6 о решении однородной системы уравнений. Если число неизвестных однородной системы n больше числа уравнений m, то система имеет хотя бы одно ненулевое решение.
Решение называется нулевым, если все его координаты равны нулю.
Д о к а з а т е л ь с т в о. Так как правые части системы равны нулю, то она имеет нулевое решение Х = (0, 0, … , 0), т. е. совместна. Если эту систему привести к равносильной разрешенной, то она будет иметь хотя бы одну свободную переменную, так как число уравнений m меньше числа неизвестных n. Свободным неизвестным можно придать ненулевые значения и получить частное ненулевое решение.
Билет № 2
2. Необходимые и достаточные условия разрешимости транспортной задачи линейного программирования.
Теорема 6.1. Для того, чтобы транспортная
задача линейного программирования
имела решение, необходимо и достаточно,
чтобы суммарные запасы поставщиков
равнялись суммарным запросам потребителей
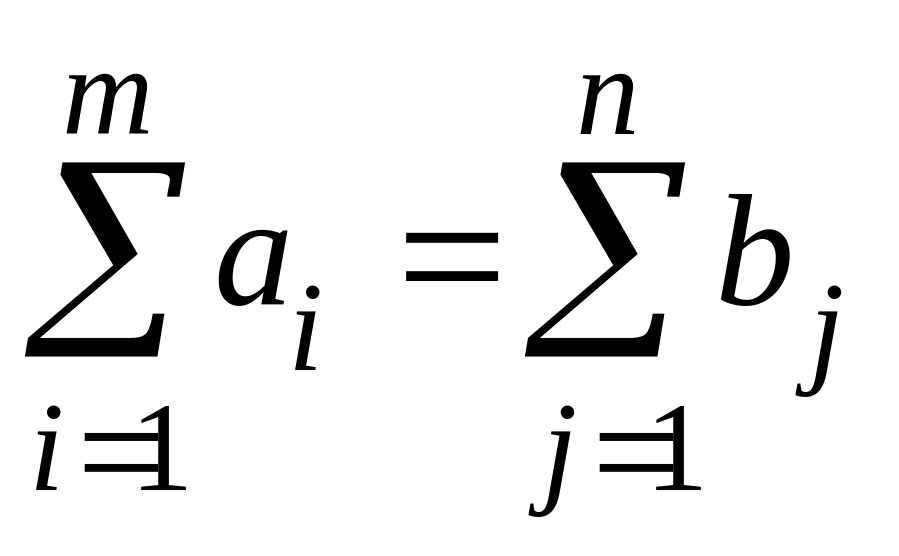 ,
т. е. задача должна быть с правильным
балансом.
,
т. е. задача должна быть с правильным
балансом.
До к а з а т е л ь с т в о. Необходимость. Пусть задача имеет допустимое решение
![]() ,
,
![]() ,
i = 1, 2, ..., m;
j = 1, 2, ..., n.
,
i = 1, 2, ..., m;
j = 1, 2, ..., n.
Докажем, что
.
Подставим
![]() в уравнения системы ограничений (6.2) и
(6.3), получим
в уравнения системы ограничений (6.2) и
(6.3), получим
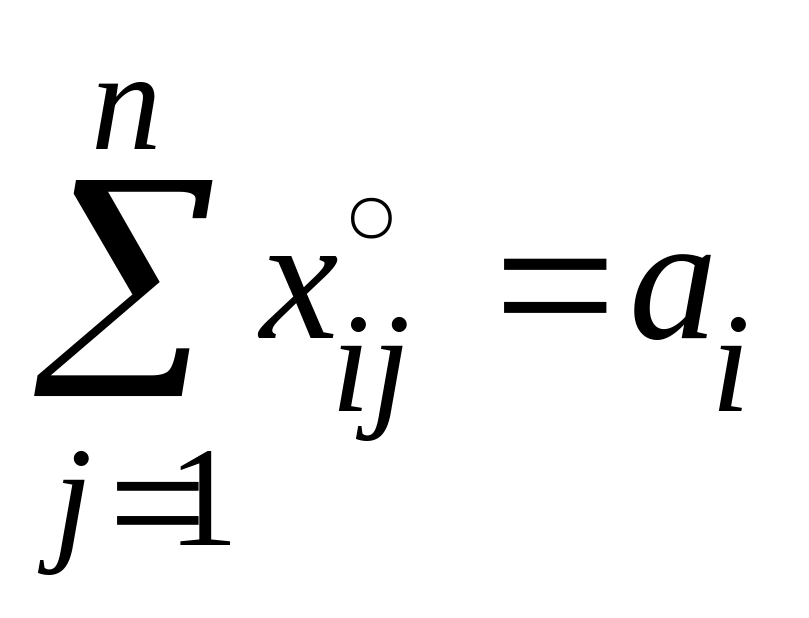 ,
i = 1, 2, ..., m,
,
i = 1, 2, ..., m,
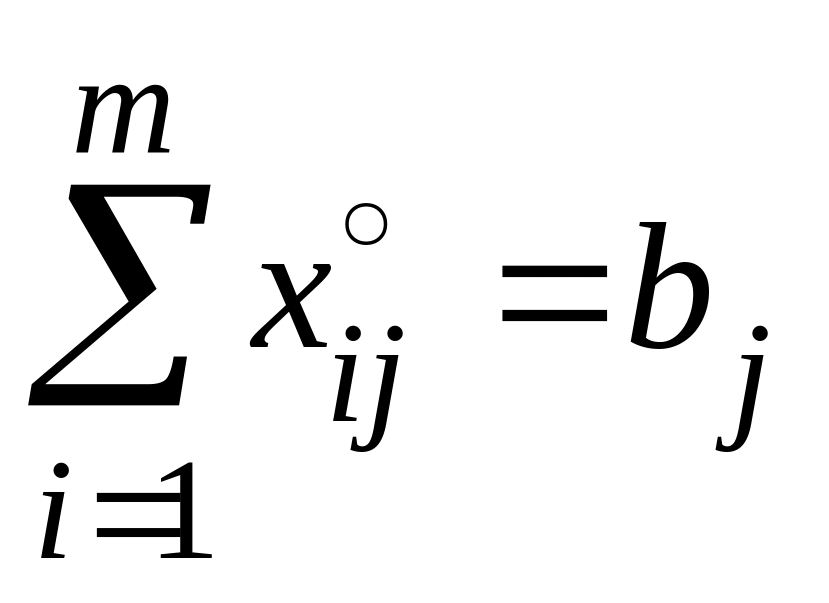 ,
j = 1, 2, ..., n
.
,
j = 1, 2, ..., n
.
Просуммируем первую и вторую группы тождеств по отдельности:
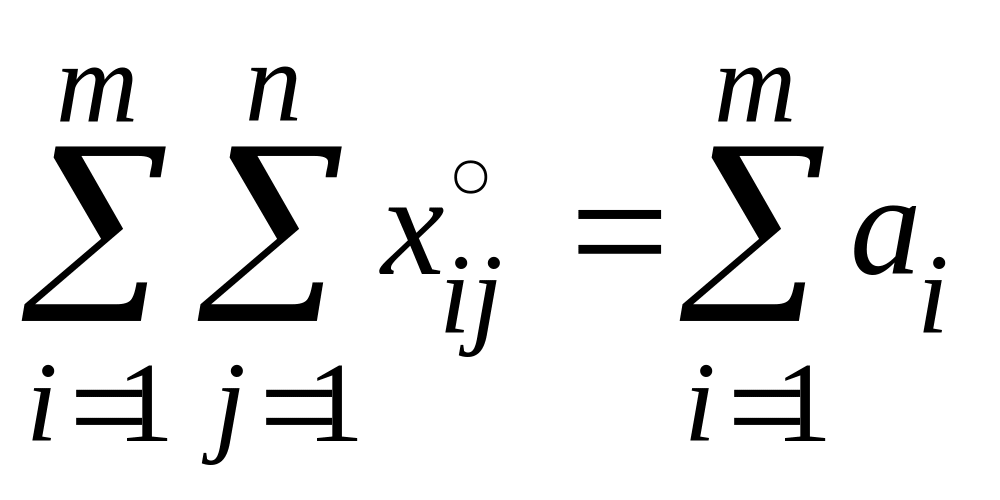 и
и
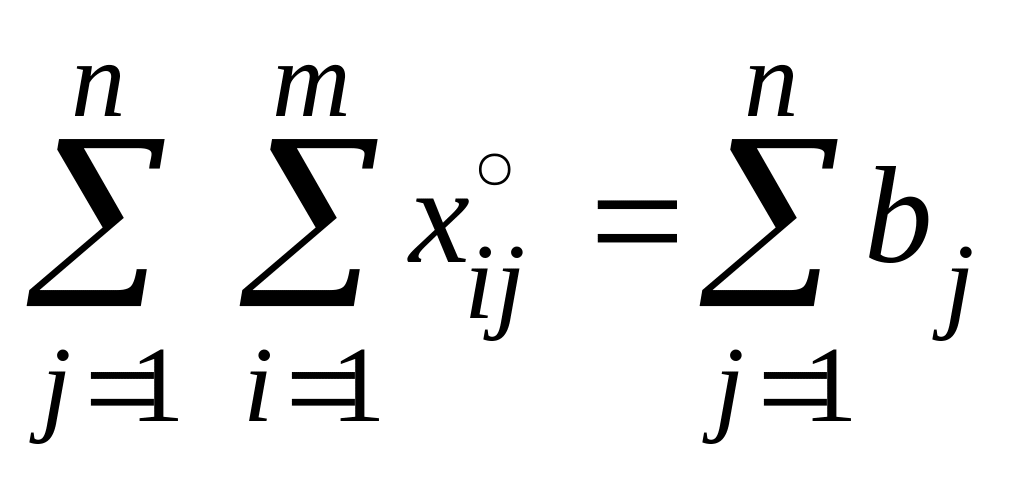 .
.
Отсюда следует, что задача имеет правильный баланс .
Достаточность. Пусть задача имеет
правильный баланс
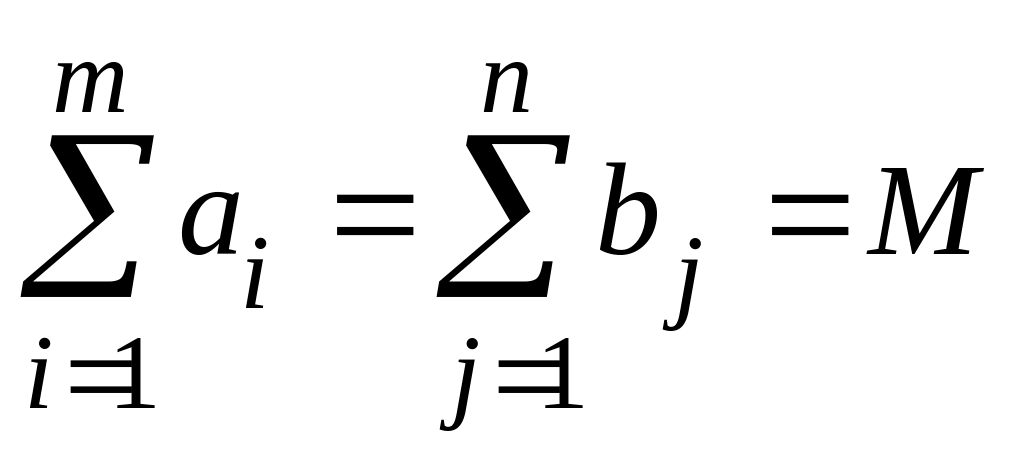 .
.
Докажем, что в этом случае задача имеет оптимальное решение.
Сначала убедимся в том, что область
допустимых решений задачи является
непустым множеством. Проверим, что
![]() ,
i = 1, 2, ..., m;
j = 1, 2, .., n
является допустимым решением. Подставим
в левые части уравнений системы
ограничений (6.2), (6.3), получим
,
i = 1, 2, ..., m;
j = 1, 2, .., n
является допустимым решением. Подставим
в левые части уравнений системы
ограничений (6.2), (6.3), получим
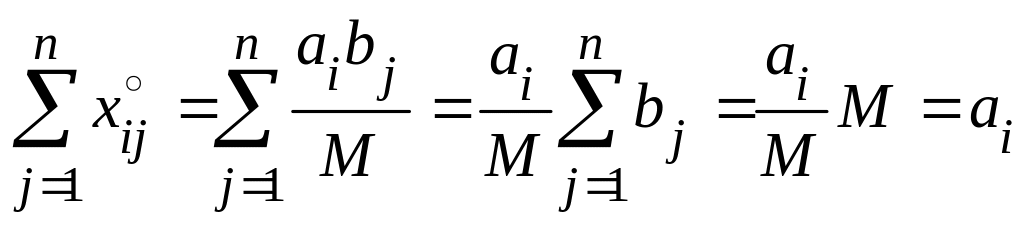 ,
i = 1, 2, ..., m,
,
i = 1, 2, ..., m,
 ,
j = 1, 2, ..., n,
,
j = 1, 2, ..., n,
т. е. уравнения обращаются в тождества.
Очевидно, что
![]() удовлетворяет и условиям неотрицательности.
удовлетворяет и условиям неотрицательности.
Далее покажем, что существует оптимальное
решение. Очевидно, стоимости перевозок
единиц груза ограничены сверху и снизу
![]() ,
где C и D
постоянные величины. Можно записать
,
где C и D
постоянные величины. Можно записать
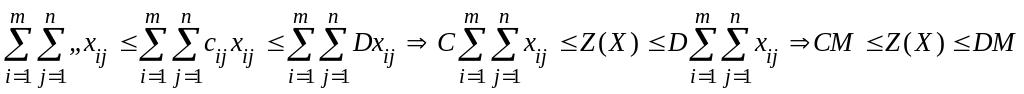 .
.
Следовательно, целевая функция ограничена на множестве допустимых решений и, как всякая непрерывная функция, достигает своего наименьшего и наибольшего значений.
Билет № 3
2. Базис системы векторов. Теорема о единственности разложения вектора по базису.
Базисом системы векторов
![]() называется такая ее подсистема
называется такая ее подсистема
![]() ,
которая линейно независимая и по которой
разлагается любой вектор системы. Здесь
r – число векторов,
входящих в базис (r
n).
,
которая линейно независимая и по которой
разлагается любой вектор системы. Здесь
r – число векторов,
входящих в базис (r
n).
Теорема 3.1. О единственности разложения векторов по базису. Любой вектор системы разлагается по базису этой системы единственным образом.
Д о к а з а т е л ь с т в о от противного.
Предположим, что имеется два разложения
вектора
![]() системы
системы
![]() по базису
по базису
![]() .
Запишем эти разложения и вычтем из
первого второе, получим
.
Запишем эти разложения и вычтем из
первого второе, получим
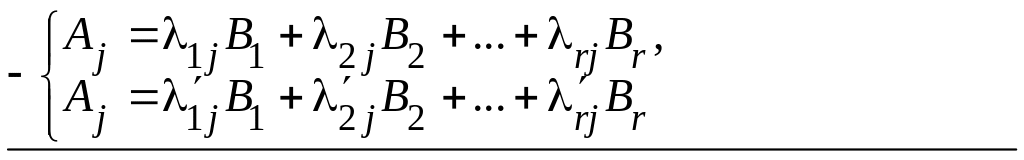
![]()
Так
как
,
образующие базис, линейно независимые,
то последнее равенство возможно только
при нулевом наборе множителей при
векторах, т. е. только при
![]() .
.