Билет № 7

2. Теорема об экстремуме целевой функции задачи линейного программирования.

Теорема 3.3. Целевая функция задачи линейного программирования достигает экстремума в угловой точке области допустимых решений; причем, если целевая функция достигает экстремума в нескольких угловых точках области допустимых решений, то она также достигает экстремума в любой выпуклой линейной комбинации этих точек.

Д о к а з а т е л ь с т в о. Будем считать, что решается задача на нахождение максимума целевой функции

Z(X) = CX max,

AX = ,

.

Докажем, что целевая функция достигает экстремума в угловой точке области допустимых решений G от противного. Если является оптимальным решением, то . Предположим, что оптимальное решение задачи не является угловой точкой (рис.3.5).

Тогда по теореме 3.1 , , (j = 1, 2, …, n) – угловые точки области G. Найдем .

Среди значений выберем наибольшее. Пусть это будет ,

т.е. = . Тогда ,

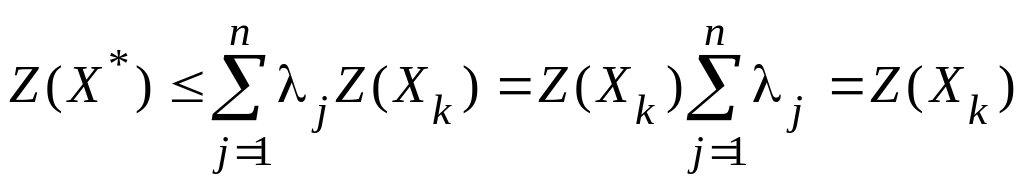что противоречит тому, что оптимальное решение в задаче на максимум. Следовательно, является угловой точкой области G.

2. Докажем второе утверждение теоремы. Пусть угловые точки области допустимых решений являются оптимальными решениями, т.е. и . Выпуклая линейной комбинации этих угловых точек равна .

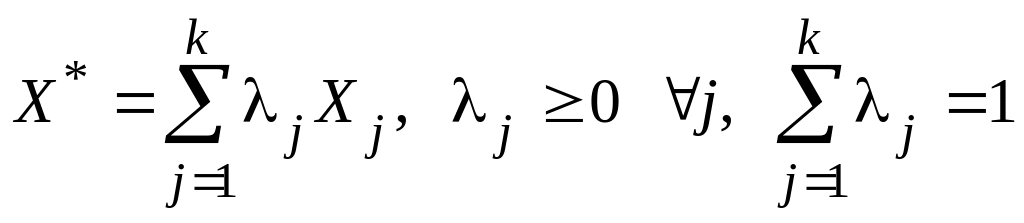Найдем значение целевой функции

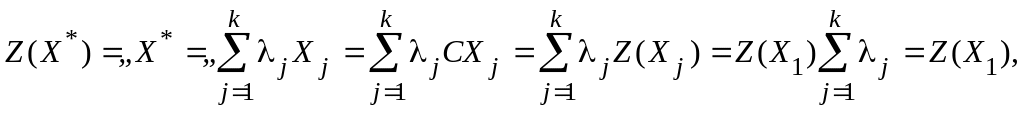
т.е. этот вектор также является оптимальным решением.

Билет № 8

2. Первая теорема двойственности.

Теорема 5.1. Если одна из пары двойственных задач имеет оптимальное решение, то и двойственная к ней имеет оптимальное решение; причем значения целевых функций задач на своих оптимальных решениях совпадают. Если же одна из пары двойственных задач не имеет решения ввиду неограниченности целевой функции, то другая не имеет решения ввиду несовместности системы ограничений.

Д о к а з а т е л ь с т в о. Пусть имеется несимметричная пара двойственных задач

Z(X) = CX max, ,

AX = ,

.

Прежде, чем приступить к доказательству, получим ряд соотношений. Предположим, что первая (прямая) из задач решалась симплексным методом и получено оптимальное решение с базисом . Запишем последнюю симплексную таблицу (табл. 5.1).

Таблица 5.1

Б				...		...	...
			1	0 ...	0	...	...
			0	1 ...	0	...	...
…	...	…	. . .	. . .	. . .	. . .	. . .	. . .
			0	0 ...	1	...	...
			0	0 ...	0	...	...

Запишем разложение вектора по базису оптимального решения

, k = 0, 1, 2, . . . , n.

Преобразуем данное разложение:

=

= ,

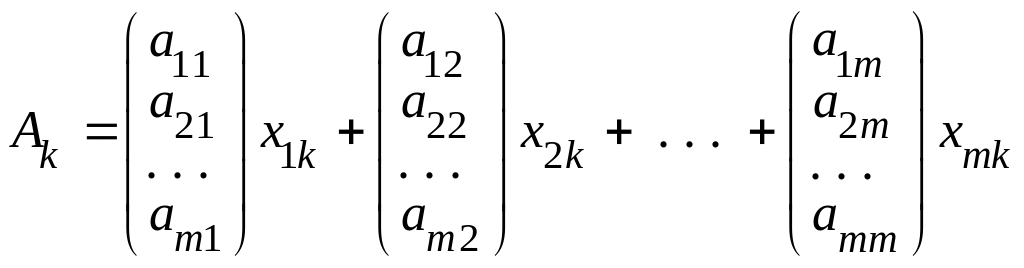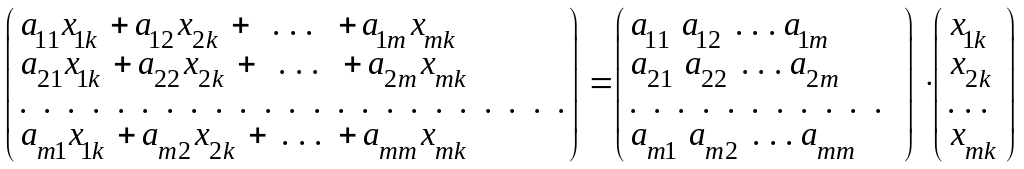k = 0, 1, 2, ..., n.

Обозначим

D = , ,

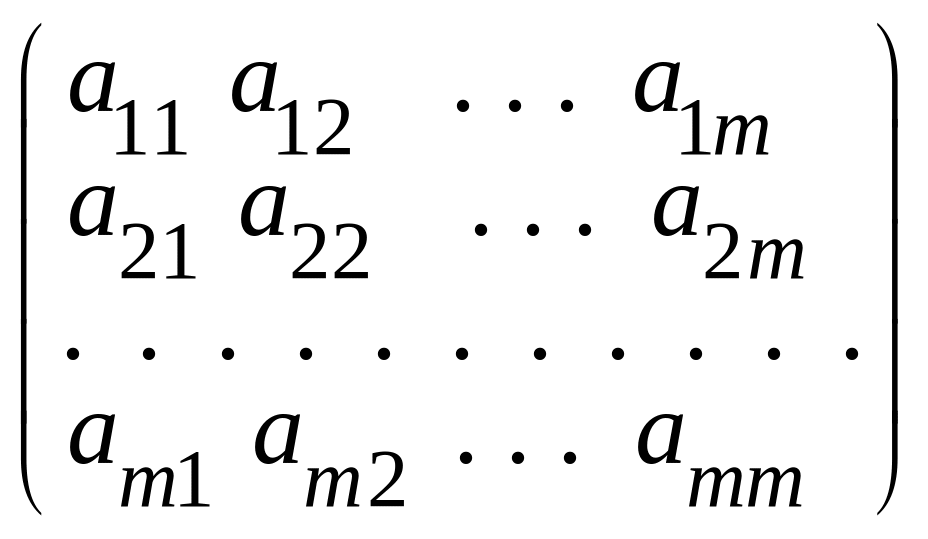тогда

, k = 0, 1, 2, ..., n. (5.11)

Умножим данное матричное равенство на обратную матрицу слева:

D .

Так как D = Е, Е = , то = , k = 0, 1, 2, ..., n. (5.12)

Аналогично можно получить

. (5.13)

Запишем с учетом полученного оценки , k = 0, 1, 2, ..., n.

В общем случае формула для расчета оценок имеет вид (4.9)

.

Обозначим через матрицу-строку коэффициентов при базисных переменных в оптимальном решении. Тогда для оценок разложений векторов-условий по базису оптимального решения имеем

. (5.14)

Обозначим матрицу, составленную из векторов , через , т.е. ; матрицу-строку из оценок через , т.е. и матрицу-строку коэффициентов целевой функции через С, т.е. . Кроме того, матрица системы уравнений-ограничений .

Получим из формул (5.12) и (5.14) следующее:

, (5.15)

. (5.16)

Теперь приступим к доказательству первого утверждения теоремы.

1. Сначала докажем, что допустимое решение двойственной задачи имеет вид

. (5.17)

Действительно, так как решение прямой задачи на максимум оптимальное, то ее оценки неотрицательные

.

Отсюда

т.е. удовлетворяет системе ограничений двойственной задачи.

2. Далее докажем, что при и

. (5.18)

Получаем .

3. Докажем, что

, (5.19)

где область допустимых решений прямой задачи,  область допустимых решений двойственной задачи.

Для этого систему ограничений прямой задачи умножим слева на допустимое решение двойственной задачи Y, а систему ограничений двойственной задачи умножим справа на допустимое решение Х исходной задачи, получим

Так как то т.е.

4. Далее докажем, что является оптимальным решением. Так как прямая задача на максимум, а  оптимальное решение, то . Двойственная задача на минимум, поэтому значение ее целевой функции на оптимальном решении должно удовлетворять условию . Как показано в пункте 3, , поэтому значение не может быть меньше , а может быть только равно . Это равенство достигается при

,

которое и является оптимальным решением двойственной задачи. Первое утверждение теоремы доказано.

Запишем полезное для нахождения оптимального решения двойственной задачи соотношение. Матричное равенство представим следующим образом

,

где  матрица обратная к матрице D, составленной из векторов-условий задачи, образующих базис оптимального решения. Матрица находится в последней симплексной таблице под единичными векторами первой симплексной таблицы, столбцами её элементов являются .

Отсюда следует, что Так как , то или

. (5.20)

Данная формула позволяет, используя оценки в последней симплексной таблицы решения прямой задачи, записывать оптимальное решение двойственной задачи как сумму оценок и коэффициентов целевой функции.

Докажем второе утверждение теоремы. Пусть прямая задача не имеет оптимального решения ввиду неограниченности целевой функции Z(X)  +. Так как и , то является пустым множеством.
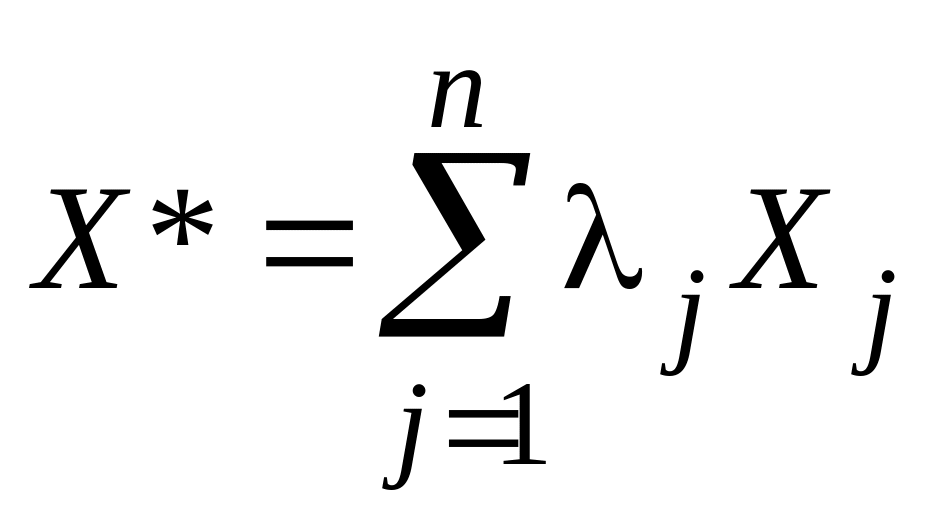
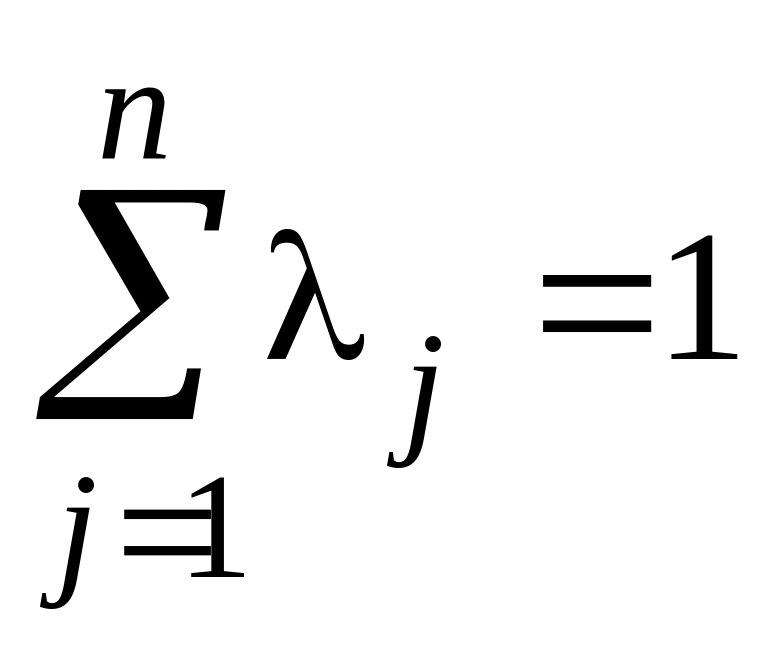