
Билет №3.
1)


2.) Обратная
матрица, алгоритм ее нахождения. Пусть
имеется квадратная матрица n-го порядка
А= .
Матрица А-1 называется обратной
по отношению к матрице А, если АА-1=А-1А=Е,
где Е – единичная матрица n-го порядка.
Обратная матрица может существовать
только для квадратных матриц, т.е. для
тех матриц, у которых число строк и
столбцов совпадает. Алгоритм нахождения
обратной матрицы.1. Запись в таблицу
для решения систем уравнений методом
Гаусса матрицу А и справа (на место
правых частей уравнений) приписать к
ней матрицу Е. 2. Используя преобразования
Жордана, привести матрицу А к матрице,
состоящей из единичных столбцов; при
этом одновременно преобразовывать
матрицу Е. 3. Если необходимо, то переставить
строки последней таблицу так, что бы
под матрицей А исходной таблицы получилась
матрица Е. 4. Записать обратную матрицу
А-1, которая находится в последней
таблице под матрицей Е в исходной
таблице. Необходимые и достаточные
условия существования обратной матрицы.
Т. Для того чтобы матрица имела
обратную матрицу необходимо и достаточно,
чтобы она была невырожденной. Матрица
называется невырожденной, если
векторы-столбцы матрицы являются линейно
независимыми. Для того чтобы существовала
обратная матрица, необходимо и достаточно,
чтобы ранг матрицы равнялся ее размерности,
т. е. r = n.Док-во. Необходимость.
Пусть матрица А имеет обратную
матрицу
.
Матрица А-1 называется обратной
по отношению к матрице А, если АА-1=А-1А=Е,
где Е – единичная матрица n-го порядка.
Обратная матрица может существовать
только для квадратных матриц, т.е. для
тех матриц, у которых число строк и
столбцов совпадает. Алгоритм нахождения
обратной матрицы.1. Запись в таблицу
для решения систем уравнений методом
Гаусса матрицу А и справа (на место
правых частей уравнений) приписать к
ней матрицу Е. 2. Используя преобразования
Жордана, привести матрицу А к матрице,
состоящей из единичных столбцов; при
этом одновременно преобразовывать
матрицу Е. 3. Если необходимо, то переставить
строки последней таблицу так, что бы
под матрицей А исходной таблицы получилась
матрица Е. 4. Записать обратную матрицу
А-1, которая находится в последней
таблице под матрицей Е в исходной
таблице. Необходимые и достаточные
условия существования обратной матрицы.
Т. Для того чтобы матрица имела
обратную матрицу необходимо и достаточно,
чтобы она была невырожденной. Матрица
называется невырожденной, если
векторы-столбцы матрицы являются линейно
независимыми. Для того чтобы существовала
обратная матрица, необходимо и достаточно,
чтобы ранг матрицы равнялся ее размерности,
т. е. r = n.Док-во. Необходимость.
Пусть матрица А имеет обратную
матрицу
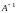 .
Покажем, что векторы-столбцы матрицы
линейно независимые. Справедливо
равенство
.
Покажем, что векторы-столбцы матрицы
линейно независимые. Справедливо
равенство
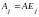 ,где
,где
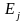 =
(0, 0, …, 0, 1, 0, …, 0)
единичный вектор.
=
(0, 0, …, 0, 1, 0, …, 0)
единичный вектор.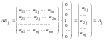 .Составим
линейную комбинацию векторов
с числовыми коэффициентами
.Составим
линейную комбинацию векторов
с числовыми коэффициентами
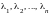 и заменим в этой комбинации все эти
векторы на
и заменим в этой комбинации все эти
векторы на
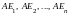 ,
получим
,
получим
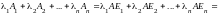
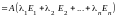 .
Покажем, что
.
Покажем, что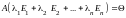 .
Умножим слева на
,
.
Умножим слева на
,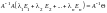 ,
,
 ,
,
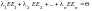 ,
,
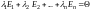 .
. линейно независимые, то последнее
равенство выполняется только при нулевом
наборе чисел
линейно независимые, то последнее
равенство выполняется только при нулевом
наборе чисел
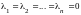 .
Достаточность. Пусть векторы
линейно независимые. Покажем, что
существует
.Любая
линейно независимая система n-мерных
векторов может служить базисом n-мерного
векторного пространства
.
Достаточность. Пусть векторы
линейно независимые. Покажем, что
существует
.Любая
линейно независимая система n-мерных
векторов может служить базисом n-мерного
векторного пространства
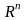 .
Поэтому
- базис
и разложить единичные векторы
.
Поэтому
- базис
и разложить единичные векторы
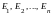 по
нему.
по
нему.
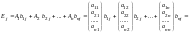
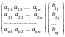 =
=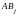 ,
(j = 1,2,…, n).Покажем,
что матрица В - обратная для матрицы
А.
,
(j = 1,2,…, n).Покажем,
что матрица В - обратная для матрицы
А.
АВ =
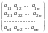
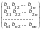 =
(
=
(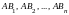 )
= (
)
= (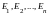 )
= Е.
)
= Е.
Решение матричных уравнений. Вид матричных уравнений: АХ=В, ХА=В, АХВ=С, где А, В и С – матрицы, Х – искомая матрица. Матричные уравнения решаются с помощью умножения уравнения на обратные матрицы. Из уравнения АХ=В: А-1АХ=В => (А-1А)Х=А-1В => ЕХ=А-1В =>Х=А-1В. Аналогично решаются другие уравнения. Из уравнения ХА=В: ХАА-1=ИА-1, Х(АА-1)=ВА-1, Х=ВА-1. Из уравнения АХВ=С: А-1АХВВ-1=А-1СВ-1, (А-1А)Х(ВВ-1)=А-1СВ-1, Х=А-1СВ-1.
Б илет
№4
илет
№4
1.)

2.)


билет №5
1.) Теорема об экстремуме целевой функции.
Целевая функция задачи лин. Порграм. Достигается экстремума в угловой точке области допустимых решений, причём, если целевая функция достигает экстремума в нескольких угловых точках области допустимых решений, то она также достигает экстремума в любой выпуклой линейной комбинации этих точек.
Доказательство. Будет считать, что решается задача на нахождение максимума целевой функции
Z(x)=CX->max,
AX=A0,
X≥Ө.
Докажем, что
целевая функция достигает экстремума
в угловой точке области допустимых
решений G от противного.
Если Х* является оптимальным решением,
то Z(X*)>Z(X)
при любом Х, принадлежащем G.
Предположим, что оптимальное решение
задачи Х* не является угловой точкой.
Тогда по теореме о выпуклости
многоугольника Х*= , ƛj≥0 при любом j,
, ƛj≥0 при любом j,
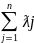 =1,
Xj (j=1,2,….,n)
– угловые точки области G.
Найдём Z(X*)=CX*=C
=1,
Xj (j=1,2,….,n)
– угловые точки области G.
Найдём Z(X*)=CX*=C Xj=
CXj=
Z(Xj). Среди
значений Z(Xj)
выберем наибольшее. Пусть это будет
Z(Xk), т.е.
maxZ(Xj)=Z(Xk).
Тогда Z(X*)≤
Z(Xk)=Z(Xk)
=Z(Xk),
что противоречит тому, что Х* оптимальное
решение в задаче на максимум. Следовательно,
Х* является угловой точкой области G.
2. Докажем второе утверждение теоремы.
Пусть угловые точки области допустимых
решений Х1, Х2, …..Хк являются оптимальными
решениями, т.е. Z(X1)=Z(X2)=…=Z(Xk)
и Z(X1)≥Z(X)
при любом х, принадлежащем G.
Выпуклая линейной комбинации этих
угловых точек равна Х* =
Xj=
CXj=
Z(Xj). Среди
значений Z(Xj)
выберем наибольшее. Пусть это будет
Z(Xk), т.е.
maxZ(Xj)=Z(Xk).
Тогда Z(X*)≤
Z(Xk)=Z(Xk)
=Z(Xk),
что противоречит тому, что Х* оптимальное
решение в задаче на максимум. Следовательно,
Х* является угловой точкой области G.
2. Докажем второе утверждение теоремы.
Пусть угловые точки области допустимых
решений Х1, Х2, …..Хк являются оптимальными
решениями, т.е. Z(X1)=Z(X2)=…=Z(Xk)
и Z(X1)≥Z(X)
при любом х, принадлежащем G.
Выпуклая линейной комбинации этих
угловых точек равна Х* =
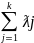 Xj,
ƛj≥0 при любом j,
=1.
Найдём значение целевой функции
Z(X*)=CX*=C
Xj,
ƛj≥0 при любом j,
=1.
Найдём значение целевой функции
Z(X*)=CX*=C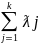 Xj=
Xj=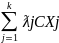 =
=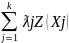 =Z(X1)
=Z(X1),
т.е. этот вектор Х* также является
решением.
=Z(X1)
=Z(X1),
т.е. этот вектор Х* также является
решением.
2.)
Собственные значения и собственные
векторы матриц. Приведение квадратной
матрицы к диагональному виду. Пусть
имеется матрица n-го
порядка
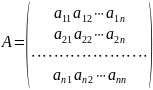 .
Собственным значением матрицы А
называется число ƛ, при которых существует
ненулевой вектор Х, удовлетворяющий
уравнению АХ=ƛХ. Собственным вектором
матрицы А, принадлежащим ее собственному
значению ƛ, называется ненулевой вектор
Х, удовлетворяющий уравнению АХ=ƛХ.
Уравнение АХ=ƛХ можно записать в виде
АХ-ƛХ= Θ или (А-ƛЕ)Х= Θ. В координатной
записи данное матричное уравнение
представляет систему уравнений с n
неизвестными
.
Собственным значением матрицы А
называется число ƛ, при которых существует
ненулевой вектор Х, удовлетворяющий
уравнению АХ=ƛХ. Собственным вектором
матрицы А, принадлежащим ее собственному
значению ƛ, называется ненулевой вектор
Х, удовлетворяющий уравнению АХ=ƛХ.
Уравнение АХ=ƛХ можно записать в виде
АХ-ƛХ= Θ или (А-ƛЕ)Х= Θ. В координатной
записи данное матричное уравнение
представляет систему уравнений с n
неизвестными
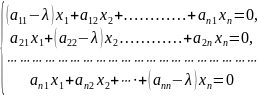
Данная
однородная система уравнений имеет
хотя бы одно ненулевое решение, если
ранг матрицы системы r(A-
ƛЕ) меньше числа неизвестных n.
Если векторы-столбцы матрицы A-
ƛЕ линейно зависимые, то ее определитель
равен нулю, т.е.
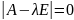 .
Данное уравнение называется
характеристическим уравнением матрицы
А. Если определитель | A-
ƛЕ | раскрыть , то получится многочлен
n-ой степени вида
а0ƛn+a1ƛn-1+…+an-1ƛ+an.
Характеристическое уравнение имеет
вид а0ƛn+a1ƛn-1+…+an-1ƛ+an=0.
Данное уравнение имеет n
корней, образующих множество ƛ(А)
собственных значений матрицы А. Св-во
1. Для любого собственного значения
ƛk(А) существует
n-rk
линейно независимых собственных векторов
F1(ƛk),
F2(ƛk),…,
Fn-rk(ƛk),
образующих фундаментальную систему
решений однородной системы уравнений
(А- ƛk Е)Х= Θ. Здесь
rk=r(А-
ƛk Е) – ранг матрицы
А- ƛk Е. Св-во 2.
Множество всех собственных векторов
А(ƛk), соответствующих
собственному значению ƛk(А)
матрицы А, совпадает с общим решением
однородной системы уравнений (А- ƛk
Е)Х= Θ, т.е. А(ƛk)={X|x=F1(ƛk)t1+F2(ƛk)t2+…+Fn-rk(ƛk)tn-rk,
t1, t2,
…,tn-rk
€ R}. Св-во 3. Любые два
собственных вектора F1(ƛk)
и F2(ƛk),
соответствующие различным собственным
значениям ƛ1≠ƛ2
характеристического уравнения | A-
ƛЕ | = 0 матрицы А, являются линейно
независимыми. Св-во 4. Система
собственных векторов, составленная из
систем собственных векторов, соответствующих
различным собственным значениям ƛ1(А),
ƛ2(А),…, ƛn(A),
является линейно зависимой. Приведение
квадратной матрицы к диагональному
виду. Говорят, что матрица А приводится
к диагональному виду с помощью матрицы
Т, если матрица Т-1АТ является
диагональной. Для нахождения матрицы
Т необходимо найти собственные значения
и собственные векторы матрицы А. Матрицу
Т составляют из собственных векторов
– столбцов. Если эта матрица является
квадратной, то матрицу А можно привести
к диагональному виду.
.
Данное уравнение называется
характеристическим уравнением матрицы
А. Если определитель | A-
ƛЕ | раскрыть , то получится многочлен
n-ой степени вида
а0ƛn+a1ƛn-1+…+an-1ƛ+an.
Характеристическое уравнение имеет
вид а0ƛn+a1ƛn-1+…+an-1ƛ+an=0.
Данное уравнение имеет n
корней, образующих множество ƛ(А)
собственных значений матрицы А. Св-во
1. Для любого собственного значения
ƛk(А) существует
n-rk
линейно независимых собственных векторов
F1(ƛk),
F2(ƛk),…,
Fn-rk(ƛk),
образующих фундаментальную систему
решений однородной системы уравнений
(А- ƛk Е)Х= Θ. Здесь
rk=r(А-
ƛk Е) – ранг матрицы
А- ƛk Е. Св-во 2.
Множество всех собственных векторов
А(ƛk), соответствующих
собственному значению ƛk(А)
матрицы А, совпадает с общим решением
однородной системы уравнений (А- ƛk
Е)Х= Θ, т.е. А(ƛk)={X|x=F1(ƛk)t1+F2(ƛk)t2+…+Fn-rk(ƛk)tn-rk,
t1, t2,
…,tn-rk
€ R}. Св-во 3. Любые два
собственных вектора F1(ƛk)
и F2(ƛk),
соответствующие различным собственным
значениям ƛ1≠ƛ2
характеристического уравнения | A-
ƛЕ | = 0 матрицы А, являются линейно
независимыми. Св-во 4. Система
собственных векторов, составленная из
систем собственных векторов, соответствующих
различным собственным значениям ƛ1(А),
ƛ2(А),…, ƛn(A),
является линейно зависимой. Приведение
квадратной матрицы к диагональному
виду. Говорят, что матрица А приводится
к диагональному виду с помощью матрицы
Т, если матрица Т-1АТ является
диагональной. Для нахождения матрицы
Т необходимо найти собственные значения
и собственные векторы матрицы А. Матрицу
Т составляют из собственных векторов
– столбцов. Если эта матрица является
квадратной, то матрицу А можно привести
к диагональному виду.
Билет №6
1.) Теоремы о взаимосвязи опорных
решений задачи линейного программирования
и угловых точек области допустимых
решений. Опорное решение –
допустимое решение для которого, векторы
условий соответствующие положительным
компонентам этого решения являются
линейно независимыми. Т. Любое
опорное решение является угловой точкой
области допустимых решений. Док-во.
Пусть
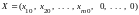 опорное решение
с базисом
опорное решение
с базисом
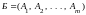 некоторой задачи с системой ограничений
некоторой задачи с системой ограничений
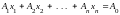 .
Предположим, что X
не является угловой точкой, тогда оно
– выпуклая линейная комбинация каких-либо
точек области допустимых решений,
например,
.
Предположим, что X
не является угловой точкой, тогда оно
– выпуклая линейная комбинация каких-либо
точек области допустимых решений,
например,
 и
и
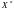 ,
т.е.
,
т.е.
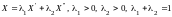 .
Так как последние n
m координат вектора
X равны нулю, а
.
Так как последние n
m координат вектора
X равны нулю, а
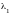 и
и
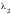 положительные, то последние n
m координат
векторов
и
также равны нулю. Подставим
положительные, то последние n
m координат
векторов
и
также равны нулю. Подставим
 в систему ограничений задачи:
в систему ограничений задачи:
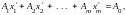
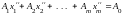 ,
,
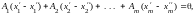
Векторы
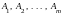 образуют базис, то они линейно независимые,
а потому данное равенство может
выполнятся только тогда, когда
образуют базис, то они линейно независимые,
а потому данное равенство может
выполнятся только тогда, когда
 Отсюда получаем
Отсюда получаем
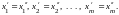 Следовательно,
Следовательно,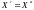 ,
и опорное решение X
не является выпуклой линейной
комбинацией каких-либо допустимых
решений, а является угловой точкой
области допустимых решений. Т. Любая
угловая точка области допустимых решений
является опорным решением. Док-во. Пусть
,
и опорное решение X
не является выпуклой линейной
комбинацией каких-либо допустимых
решений, а является угловой точкой
области допустимых решений. Т. Любая
угловая точка области допустимых решений
является опорным решением. Док-во. Пусть
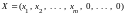 угловая точка области допустимых решений
и
угловая точка области допустимых решений
и
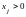 при
j = 1, 2,…, m.
Чтобы доказать, что это решение - опорное,
достаточно показать, что векторы
при
j = 1, 2,…, m.
Чтобы доказать, что это решение - опорное,
достаточно показать, что векторы
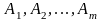 ,
соответствующие положительным
координатам решения, являются линейно
независимыми. Пусть векторы линейно
зависимы. Тогда существует ненулевой
набор чисел
,
соответствующие положительным
координатам решения, являются линейно
независимыми. Пусть векторы линейно
зависимы. Тогда существует ненулевой
набор чисел
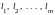 такой, что
такой, что

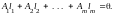 Так как X
допустимое решение, то имеет место
равенство
Так как X
допустимое решение, то имеет место
равенство
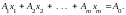
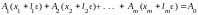 ,
т.е.
,
т.е.
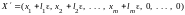 - решение системы ограничений задачи.
Аналогично доказываем, что решением
системы является также вектор
- решение системы ограничений задачи.
Аналогично доказываем, что решением
системы является также вектор
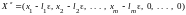 .
Для того, чтобы векторы
и
удовлетворяли условиям неотрицательности,
выберем , что
.
Для того, чтобы векторы
и
удовлетворяли условиям неотрицательности,
выберем , что
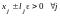 .
Это возможно, так как
при
j = 1, 2,…, m..
При таком выборе числа
векторы
и
являются
допустимыми. Нетрудно видеть, что
.
Это возможно, так как
при
j = 1, 2,…, m..
При таком выборе числа
векторы
и
являются
допустимыми. Нетрудно видеть, что
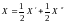 ,
т.е. X - выпуклая
линейная комбинация
и
.
Это противоречит тому, что X
является угловой точкой. Следовательно,
векторы
линейно независимые, и решение X
является опорным.
,
т.е. X - выпуклая
линейная комбинация
и
.
Это противоречит тому, что X
является угловой точкой. Следовательно,
векторы
линейно независимые, и решение X
является опорным.
2.) Квадратичная форма: ее стандартный вид, изменение при невырожденном линейном преобразовании, канонический вид. Знакоопределенность квадратичных форм. Критерий Сильвестра. Квадратичной формой n переменных x1,x2,…,xn называется функция F(x1,x2,…,xn), представляющая собой сумму, каждое слагаемое которой имеет вторую степень относительно этих переменных. Обычно используют квадратичные формы следующего вида(cтандартная форма):
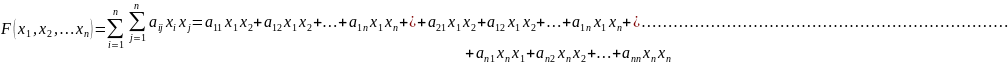
Матрица данного вида называется матрицей квадратичной формы.
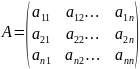 .Матрица
является симметрической, т.к. aij=aji
i,j=1,2,…,n.
Квадратичная форма в векторно-матричном
виде: F(x)=XTAX,
где
.Матрица
является симметрической, т.к. aij=aji
i,j=1,2,…,n.
Квадратичная форма в векторно-матричном
виде: F(x)=XTAX,
где
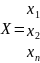
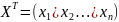 .
.
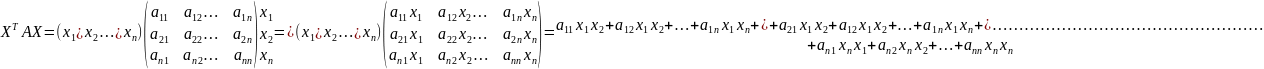 Преобразование
квадратичной формы при невырожденном
линейном преобразовании координат.
X=CY,
,
Преобразование
квадратичной формы при невырожденном
линейном преобразовании координат.
X=CY,
,
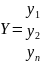 ,
, .
Здесь
x1
,
x2
,
…, xn
– старые переменные, y1
,
y2
,
…, yn -новые
переменные, С – матрица преобразования
координат. Преобразование координат
называется невырожденным, если матрица
преобразования С невырожденная.
Квадратичная форма F(x)=XTAX
в новой системе координат примет вид
F(Y)=
(CY)TA(CY)=YTCTACY=YTA*Y,
где A*=CTAC-
матрица квадратичной формы в новой
системе координат. Канонический
вид квадратичной формы.
Квадратичная
форма называется канонической, если
все ее коэффициенты aij
при
i
≠ j
равны нулю, т.е. она имеет вид:
.
Здесь
x1
,
x2
,
…, xn
– старые переменные, y1
,
y2
,
…, yn -новые
переменные, С – матрица преобразования
координат. Преобразование координат
называется невырожденным, если матрица
преобразования С невырожденная.
Квадратичная форма F(x)=XTAX
в новой системе координат примет вид
F(Y)=
(CY)TA(CY)=YTCTACY=YTA*Y,
где A*=CTAC-
матрица квадратичной формы в новой
системе координат. Канонический
вид квадратичной формы.
Квадратичная
форма называется канонической, если
все ее коэффициенты aij
при
i
≠ j
равны нулю, т.е. она имеет вид:
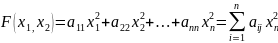
Матрица
такой квадратичной формы является
диагональной
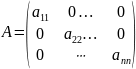 .
Т.
Любая квадратичная форма может быть
приведена к каноническому виду с помощью
невырожденного линейного преобразования.
Знакоопределенность
квадратичной формы. Канонический
вид квадратичной формы определяется
неоднозначно. Т.
Число слагаемых с положительными
(отрицательными) коэффициентами
канонической квадратичной формы не
зависит от способа приведения формы к
этому виду. РАНГОМ квадратичной формы
называется отличных от нуля коэффициентов
в ее каноническом виде. Ранг квадратичной
формы совпадает с рангом матрицы
квадратичной формы. Квадратичная форма
называется положительно (отрицательно)
определенной, если она принимает
положительные(отрицательные) значения
в любой точке n-мерного
пространства
.
Т.
Любая квадратичная форма может быть
приведена к каноническому виду с помощью
невырожденного линейного преобразования.
Знакоопределенность
квадратичной формы. Канонический
вид квадратичной формы определяется
неоднозначно. Т.
Число слагаемых с положительными
(отрицательными) коэффициентами
канонической квадратичной формы не
зависит от способа приведения формы к
этому виду. РАНГОМ квадратичной формы
называется отличных от нуля коэффициентов
в ее каноническом виде. Ранг квадратичной
формы совпадает с рангом матрицы
квадратичной формы. Квадратичная форма
называется положительно (отрицательно)
определенной, если она принимает
положительные(отрицательные) значения
в любой точке n-мерного
пространства
 , кроме начала координат, т.е.
, кроме начала координат, т.е.
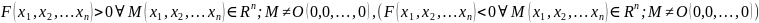 .
Т.
Для того чтобы квадратичная форма
F(Х)=XTAX
была положительно(отрицательно)
определенной, необходимо и достаточно,
чтобы все собственные значения матрицы
А были положительные(отрицательные).
Критерий
Сильвестра. Т.
Для того чтобы квадратичная форма была
положительно определенной, необходимо
и достаточно, чтобы все главные миноры
матрицы этой формы были положительны,
т.е.
.
Т.
Для того чтобы квадратичная форма
F(Х)=XTAX
была положительно(отрицательно)
определенной, необходимо и достаточно,
чтобы все собственные значения матрицы
А были положительные(отрицательные).
Критерий
Сильвестра. Т.
Для того чтобы квадратичная форма была
положительно определенной, необходимо
и достаточно, чтобы все главные миноры
матрицы этой формы были положительны,
т.е.
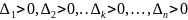 ,
где
,
где
 (k=1,2,…,n)
(k=1,2,…,n)
Т.
Если квадратичная форма удовлетворяет
критерию Сильвестра, то она может быть
приведена к каноническому виду

