1. Понятие геометрического вектора.Равенство векторов.Сложение векторов.

Упорядоченный набор n действительных чисел 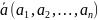будем называть n- мерным вектором, его элементы 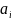(i = 1, 2, …, n) назовем компонентом вектора, n – размерность вектора

Геометрическим вектором называется направленный отрезок, который можно перемещать параллельно ему самому.

Направленный отрезок с началом в точке A и концом в точке B обозначается AB. Векторы обозначаются строчными латинскими буквами со стрелками: → a , → r , → x Операции над векторами:

Равенство В.

Будем говорить, что 2 вектора 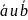равны между собой 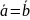, если они имеют одинаковую размерность n и их соответствующие компоненты равны, т.е

Два вектора называются равными, если они совмещаются параллельным переносом.

Т.е. существует такой параллельный перенос, при котором начало и конец одного вектора совмещается с началом и концом другого вектора соответственно.

Сумма векторов.

Суммой двух векторов   и   называется вектор  , направленный из начала вектора   в конец вектора   при условии, что начало  совпадет с концом вектора  . Если векторы заданы их разложениями по базисным ортам, то при сложении векторов складываются их соответствующие координаты.

Суммой векторов , имеющих одинаковую размерность, является вектор:

2.Умножение вектора на число.Свойства операций сложения и умножения.

Геометрически произведение   ненулевого вектора   на число k – это вектор, длина которого равна ka, где a =   – длина данного вектора, а направление, приa  0, совпадает с направлением вектора  , если k > 0 и противоположно, если k < 0. Если хотя бы один из сомножителей – вектор или число – равен нулю, то и произведение равно нулю.

При умножении вектора на число каждая из его координат умножается на это число.

Для любых векторов a,b,c и любых вещественных чисел   α, β выполняются следующие свойства:

1) a+b= b+a (свойство коммутативности операции сложения);  2)(a+b ) +c =a+( b+c)(свойство ассоциативности операции сложения); 

3) a+0 =a ;  4) a+(-a)=0 ;  5)   (свойство ассоциативности по отношению к числам);  6)   (свойство дистрибутивности по отношению к умножению на число);  7)   (свойство дистрибутивности по отношению к умножению на вектор;  8)   .

3. Скалярное произведение и его свойства. Длина вектора. Определение. Скалярным произведением векторов и называется число, равное произведению длин этих сторон на косинус угла между ними.

 = | || |cos

Свойства скалярного произведения:

1)  = | ²;

2)  = 0, если  или = 0 или = 0.

3)  =  ;

4) ( + ) =  +  ;

5) (m ) = (m ) = m(  ); m=const

Длиной ненулевого вектора называется длина отрезка AB. Длина вектора (вектора ) обозначается так: . Длина нулевого вектора считается равной нулю: .

1.если на плоскости заданы точки и , то вектор имеет координаты и его длина вычисляется по формуле:

2.длины вектора по координатам:

4. Декартова система координат. Действия с векторами в этой системе

Прямоугольной декартовой системой координат на плоскости называется совокупность двух взаимно перпендикулярных числовых осей Ox и Oy с общей начальной точкой O. Числовые оси называются осями координат, а именно: ось Ox – осью абсцисс, ось Oy – осью ординат. Точка O называется началом координат. Пусть A – произвольная точка плоскости, отличная от начала координат, Ax и Ay – основания перпендикуляров, опущенных из точки A соответственно на оси абсцисс и ординат (в случае, если A лежит на одной из осей, например, абсцисс, под Ax понимается сама точка A, а Ay совпадает с точкой O). Абсциссой точки A называется координата x точки Ax на оси абсцисс, а ординатой точки A – координата y точки Ay на оси ординат. Координатами точки плоскости называются ее абсцисса и ордината, взятые в указанном порядке. Обе координаты точки O, начала координат, очевидно, равны нулю. При необходимости указать, что точка A имеет координаты x и y будем записывать A (x; y). Плоскость с введенной декартовой системой координат называется плоскостью Oxy.

СВОЙСТВА ДЕЙСТВИЙ НАД ВЕКТОРАМИ

Операции сложения векторов и умножения вектора на число обладают след. свойствами:

1) ,

2) ,

3) ,

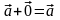4) ,

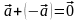5) ,

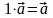6) ,

7) ,

8) .

5. N-мерные вектора. Действия с n-мерными векторами

N-мерным вектором называется последовательность n чисел. Эти числа называются координатами вектора. Число координат вектора n называется размерностью вектора.

Действия над векторами:

Умножение вектора на число

Любой n-мерный вектор А можно умножить на любое число λ, при этом все его координаты умножаются на это число:

λA=(λ*a1, λ*a2,..., λ*an)

Действия над векторами

Умножение вектора на число

Любой n-мерный вектор А можно умножить на любое число λ, при этом все его координаты умножаются на это число:

λA=(λ*a1, λ*a2,..., λ*an)

Сложение векторов

Два вектора одинаковой размерности можно сложить, при этом их соответствующие координаты складываются:

Свойства линейных операций:

А + В = В + А

(А + В) + С = А+(В + С)

λ(А + В) = λА + λВ

(λ+ μ)А = λА + μ А

λ(μ А) = (λμ)А

Скалярное произведение векторов

Скалярным произведением векторов и называется величина, вычисляемая по формуле:

Модуль (длина) вектора

Угол между векторами

6. Т-ма о числ.соотнош.между 2-мя в-рами. Если А и В есть n-мерные в-ра, то справедлива следующие соотношения:

1) |K*A|=|K|*|A|, где К-число

2) |A*B|≤|A|*|B| нер-во Коши-Буняковского

3) |A+B|≤|A|+|B| нер-во треугольника

Д-ва:

1)|kA| = √(kA)(kA)= √k²(AA)= √k²√AA=|k||A|

2)C = A²B – A(AB); A²=k, AB=l; выраз. С², обрат.замена; C²≥0 => A²(A²B² – (AB)²)≥0, т.к. A²≥0, A²B² – (AB)²≥0  A²B²≥(AB)²; извл.корень |AB| ≤ |A||B|

3) Т.к. AB≤|AB|, |AB|≤|A||B|, то AB≤|A||B|. |A+B|²=(A+B)²=A²+2AB+B²≤|A|²+2|A||B|+|B|²=(|A|+|B|)², т.е. |A+B|²≤(|A|+|B|)²  |A+B|≤|A|+|B|

n-мерный в-р, длина которого равна единице, называется нормированным.