11.2. Динамические нагрузки

Эти нагрузки характерны для транспортных машин. Действие таких нагрузок заставляет принимать во внимание усталостную прочность материала.

а) б) в)

г) д)

Рис.11.1. Виды динамической нагрузки

а) симметричный цикл; б) пульсирующий цикл; в) несимметричный цикл ; г) случайная

нагрузка (широкополосный спектр);д) случайная нагрузка узкополосный спектр).

На рис.11.1 представлены графики изменения во времени типичных видов нагрузки. При этом первые три чаще всего носят искусственный характер и используются при испытаниях материалов, деталей и узлов машин. Случайная нагрузка наиболее характерна на практике. Ее рассмотрим более подробно.

11.2.1. Нагрузка как случайный процесс

Случайный процесс представляет собой случайную величину зависящую от времени. На рис.11.1.г показана одна реализация какого то случайного процесса. Сам же случайный процесс представляет собой бесконечное множество реализаций. Таким образом, мы не можем наблюдать весь случайный процесс, а лишь определенное число его реализаций. При этом значения случайного процесса взятые в определенный момент времени (временное сечение) будут представлять собой выборку случайных чисел, к которой применимы все статистические оценки и выводы. В частности, могут быть построены вероятностные распределения, а так же оценены моменты (математическое ожидание, дисперсия и т.д.). Кроме того могут быть оценены многомерные вероятностные распределения случайных величин и взаимосвязи (корреляция) между случайными величинами в различных временных сечениях.

Для характеристик случайного процесса X(t) справедливы следующие формулы:

математическое ожидание

,

где f(x,t) - закон распределения (плотность вероятности) процесса;

дисперсия

;

корреляционная (автокорреляционная) функция

,

где f₂(x₁,x₂;t₁,t₂) - двумерный закон распределения значений случайной функции X(t), взятых в двух временных сечениях t₁ и t₂.

Следует различать два важных свойства процесса: стационарность и эргодичность. Стационарность означает однородность во времени вероятностных свойств процесса. Функцию X(t) называют стационарной в узком смысле, если все ее многомерные плотности вероятности f_n(x₁, . . . ,x_n;t₁, . . . ,t_n) при любом n зависят только от интервалов t₂-t₁, . . . ,t_n-t₁ и не зависят от положения этих интервалов в области изменения аргумента t. Это очень жесткое требование на практике заменяют более мягким определением, которое получило название стационарности в широком смысле. Соглаcно этому определению функция стационарна, если ее математическое ожидание постоянно, а корреляционная функция зависит только от разности аргументов т.е.

_x(t) = const, K_x(t₁,t₂) = K_x(t₁-t₂) = K_x().

Таким образом корреляционная функция для стационарного случайного процесса является функцией одной переменной. Кроме того, для нее характерны три следующих свойства:

1. K_x(0)=D_x(t)=D_x , т.е. дисперсия постоянна и равно значению K_x() при =0;

2. K_x(-)=K_x(), т.е. корреляционная функция четна;

3. | K_x()|K_x(0)=D_x, т.е. значения корреляционной функции не превышают D_x.

Если рассматривать два случайных процесса X(t) и Y(s), то можно говорить о взаимной корреляционной функции

.

Понятие эргодичности связано с возможностью замены оценки статистических свойств процесса по совокупности его реализаций оценкой по одной реализации. Таким образом для эргодического процесса по одной реализации длительностью T можно определять моменты вплоть до n-го порядка на основе следующей формулы:

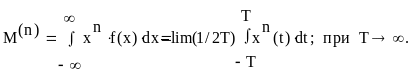
Стационарные случайные функции могут обладать свойством эргодичности по отношению к моментам не всех порядков. На практике для описания случайных функций используются как правило математическое ожидание, дисперсия и корреляционная функция, т.е. моменты первого и второго порядков. По этой причине стационарную случайную функцию можно считать эргодичной, если она эргодична по отношению к этим характеристикам процесса. Об эргодичности или неэргодичности случайного процесса можно судить по виду его корреляционной функции. Если корреляционная функция процесса стремится к нулю при , то это является достаточным условием для того, чтобы считать процесс эргодическим относительно моментов второго порядка. Характерный вид корреляционной функции стационарного эргодического процесса представлен на рис.11.2.

Рис.11.2. Типичный вид корреляционной функции стационарного эргодического

процесса

Всякая эргодическая функция является стационарной, но не наоборот. Рассмотренный ниже пример иллюстрирует один практически важный случай математической модели для случайной нагрузки.

Пример 11.1. Действующая нагрузка представляет собой сумму некоррелированных между собой стационарной эргодичной случайной функции и случайной величины z(t)=x(t)+y. Требуется показать, что z(t) не обладает свойствами эргодичности.

Решение.

Функция z(t) не является эргодической, т.к. математическое ожидание каждой ее новой реализации будет зависеть от того, какое значение приняла случайная величина y в начальный момент времени. Таким образом по одной реализации мы не сможем получить достоверную оценку математического ожидания процесса. Математическое ожидание случайной функции z(t) определяется по формуле

_z(t)= _x(t)+ _y.

Корреляционная функция для z(t) с учетом некоррелированности x(t) и y будет равна

.

В этом выражении точки над символами означают, что соответствующие случайные величины или функции центрированы, т.е., например и т.д.

Другим доказательством неэргодичности процесса является то, что при  корреляционная функция стремится к постоянной величине D_y отличной от нуля. Заметим, что z(t) при этом будет стационарным.