8.3. Доверительные интервалы и вероятности

Для определения точности оценок в статистике пользуются доверительными интервалами, а для определения надежности оценок - доверительными вероятностями. Эти понятия связаны между собой.

Рассмотрим доверительный интервал для оценки среднего значения нормально распределенной величины X:

,

тогда доверительная вероятность (1  ) это вероятность того, что истинное значение математического ожидания находится внутри доверительного интервала

(1  ) = P(   < _x < + ) = P( _x < ).

Величина  называется уровнем значимости.

При этом можно решать следующие две задачи:

а) по заданному  или P определяют  ;

б) по заданному  определяют P.

Если случайная величина X распределена нормально и ее стандартное отклонение S_x (а не его оценка) известно и, если верхняя и нижняя границы доверительного интервала симметричны относительно среднего значения, тогда

,

где Z_(1-/2) - это (1 - /2) 100 процентная точка (квантиль) стандартного (нормированного) нормального распределения; S_x - стандартное отклонение величины X ; n- размер выборки.

Этот результат вытекает из рассмотрения нормированной случайной величины, распределенной по нормальному закону

,

где - стандартное отклонение оценки среднего значения.

Действительно

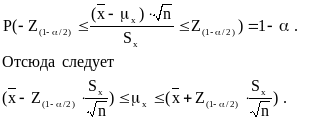
Пример 8.3. Если принять уровень значимости 5%, т.е.  = 0,05 (или 95% доверительная вероятность), то, полагая для примера 8.2, что дисперсия в нем определена точно, получим

(1 -/2) = (1 - 0,025) = 0,975.

По таблице определим Z_(1-/2) = 1,96, тогда .

Таким образом с 95% уровнем доверия истинное значение математического ожидания лежит в интервале

[(3,85 - 0,31) - (3,85 + 0,31)] = [3,51 - 4,16].

Пример 8.4. Если предыдущий пример решать с  = 0,01 (т.е. 99% доверительная вероятность), тогда

(1 -/2) = (1 - 0,005) = 0,995.

По таблице находим Z_(1-/2) = 2,58, тогда

Таким образом доверительный интервал при увеличении доверительной вероятности расширился и стал

[3,435 - 4,265].

4. Доверительный интервал для математического ожидания случайной

величины, распределенной нормально с неизвестным стандартным

отклонением

Для решения этой задачи используется распределение Стьюдента, именуемое также Т-распределением. (Student - псевдоним В.Госсета, впервые применившего это распределение для задач статистики). Доказано, что случайная величина Т

,

где и - выборочные (размер выборки n) среднее и стандарт случайной величины X, распределенной нормально, подчиняется распределению Стьюдента с (n-1) степенью свободы.

Плотность распределения Стьюдента с (n-1) степенью свободы имеет вид

.

Подставляя в выражение для доверительной вероятности

(1  ) = P(  _x < ),

выражение для случайной величины Т получим

(1  ) = P(T < t_{(1-/2), n-1}),

где t_{(1-/2), n-1} - это (1 - /2) 100 - процентная точка (квантиль) Т-распределения. Ее значение определяют по таблицам интегрального закона Т-распределения .

Полуширина доверительного интервала, соответствующего уровню значимости , имеет вид

 = t_{(1-/2), n-1}^. / .

Пример 8.5. Выборка из семи измерений пружин со средней жесткостью 9,25 кН/см и с выборочным стандартным отклонением 0,18 кН/см. Полагая распределение жесткости нормальным, определить доверительный интервал для 5% уровня значимости.

Решение.

По таблице Т-распределения находим t_0,975;6 = 2,447, тогда  = 2,447^. 0,18/7 = 0,166. Таким образом доверительный интервал имеет вид

[9,25 - 0,166 ; 9,25 + 0,166] = [9.084 ; 9,416].