33)Круговой процесс. Цикл Карно. Кпд цикла Карно.
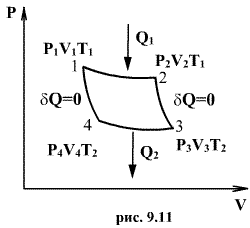
Анализируя работу тепловых двигателей, французский инженер С. Карно в 1824г. пришел к выводу, что наивыгоднейшим круговым процессом является обратимый круговой процесс, состоящий из двух изотермических и двух адиабатических процессов, т.к. он характеризуется наибольшим коэффициентом полезного действия. Такой цикл получил название цикла Карно. В прямом цикле Карно рабочее тело изотермически, а затем адиабатически расширяется, после чего снова изотермически (при более низкой температуре) и потом адиабатически сжимается. Т.е. цикл Карно ограничен двумя изотермами и двумя адиабатами.
При
изотермическом расширении от нагревателя
отбирается тепло 
(на
участке 1-2 рис. 9.11). Вследствие этого
температура газа поддерживается
неизменной. Соответственно, параметры
точки 2 будут равны 
.
На участке 2-3 происходит адиабатное
расширение. Внутренняя энергия газа
уменьшается и его температура падает
до Т2. Параметры точки 3 - 
.
На участке 3-4 газ изотермически сжимается.
Параметры точки 4 - 
.
Выделяющееся при этом тепло 
отбирается
холодильником. Участок 4-1 -адиабатическое
сжатие до исходного состояния,
соответствующего точке 1. Таким образом,
завершен цикл “1-2-3-4-1 и в итоге нагреватель
отдал газу теплоту
,
а холодильник отобрал
Разность 
определяет
полезную работу газа за один цикл, так
как согласно I началу термодинамики 
,
но для кругового процесса 
и,
следовательно 
.
Отношение
полезной работы к затраченной энергии
нагревателя определяет коэффициент
полезного действия (к.п.д.) тепловой
машины:
34)Уравнения состояния идеальных газов. Уравнение Ван-дер-Ваальса.
В МКТ и термодинамике идеального газа макроскопическими параметрами являются: p, V, T, m.
Мы
знаем, что 
.
Следовательно, 
.
Учитывая, что 
,
получим: 
.
Произведение
постоянных величин есть величина
постоянная, следовательно: 
- универсальная газовая постоянная (универсальная, т.к. для всех газов одинаковая).
Таким
образом, имеем: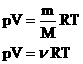
-
уравнение состояния (уравнение Менделеева
– Клапейрона).
Если n=1
моль, то, обозначив объем одного моля Vм,
получим: 
.
Для нормальных условий получим:
Запись
уравнения через плотность: 
-
плотность зависит от температуры и
давления!
Часто
необходимо исследовать ситуацию, когда
меняется состояние газа при его неизменном
количестве (m=const) и в отсутствие химических
реакций (M=const). Это означает, что количество
вещества n=const. Тогда: 
Для
постоянной массы идеального газа
отношение произведения давления на
объем к абсолютной температуре
в данном состоянии есть величина
постоянная: 
.
Ван-дер-Ваальсом в уравнение Клапейрона — Менделеева введены две поправки.
1. Учет собственного объема молекул. Наличие сил отталкивания, которые противодействуют проникновению в занятый молекулой объем других молекул, сводится к тому, что фактический свободный объем, в котором могут двигаться молекулы реального газа, будет не Vm, а Vm — b, где b — объем, занимаемый самими молекулами.
Объем b равен учетверенному собственному объему молекул. Если, например, в сосуде находятся две молекулы, то центр любой из них не может приблизиться к центру другой молекулы на расстояние, меньшее диаметра d молекулы. Это означает, что для центров обеих молекул оказывается недоступным сферический объем радиуса d, т. е. объем, равный восьми объемам молекулы или учетверенному объему молекулы в расчете на одну молекулу.
2.
Учет притяжения молекул. Действие сил
притяжения газа приводит к появлению
дополнительного давления на газ,
называемого внутренним давлением. По
вычислениям Ван-дер-Ваальса, внутреннее
давление обратно пропорционально
квадрату молярного объема, т. е.
где а — постоянная Ван-дер-Ваальса, характеризующая силы межмолекулярного притяжения, Vm — молярный объем.
Вводя
эти поправки, получим уравнение
Ван-дер-Ваальса для моля газа (уравнение
состояния реальных газов):
Для произвольного количества вещества v газа (v=m/M) с учетом того, что V=vVm, уравнение Ван-дер-Ваальса примет вид
