2. Вариационный принцип Гамильтона

Уравнения Гамильтона (44) могут быть получены из вариационного принципа, сформулированного относительно функционала действия механической системы вида

                                                             (46)

при условиях, аналогичных (1.3), только теперь сформулированных для точек фазового пространства

_­ .                                               (47)

Вариация действия (46), при которой подынтегральная функция рассматривается как функция совокупностей независимых переменных, собранных в контравариантный вектор q и ковариантный вектор p, запишется следующим образом:

.

Так как операции варьирования и дифференцирования по времени перестановочны, то

.

Первое слагаемое обращается в нуль при условиях (47), а из равенства нулю второго слагаемого вытекают уравнения Гамильтона (44).

3. Дифференцирование величин по времени. Законы сохранения

С учетом уравнений движения (44), можно получить, что

.                                                          (48)

Если явная зависимость функции Гамильтона (и, соответственно функции Лагранжа) от времени отсутствует, то выполняется закон сохранения энергии: вдоль фазовой траектории системы выполняется условие dH/dt = 0.

В общем случае, если вычислить полную производную по времени для любой функции времени, обобщенных координат и импульсов f(q,p,t) механической системы вдоль ее фазовой траектории, то эта производная с помощью уравнений Гамильтона (44) может быть записана в виде

,                                                    (49)

где введено обозначение

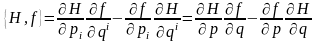,                                  (50)

называемое скобкой Пуассона функции Гамильтона H и функции f.

Скобки Пуассона играют первостепенную роль в случае записи закона сохранения некоторой физической величины, явно не зависящей от времени. Именно, по определению, закон сохранения физической величины f(p,q,t) для некоторой механической системы с обобщенными координатами и обобщенными импульсами имеет следующий вид:

.                                                         (51)

В случае, когда f(p,q,t) = f(p,q) явно от времени не зависит, согласно (49) переходит в условие

.                                                             (52)

В частности, если функция Гамильтона системы Н не зависит явно от времени, то она является сохраняющейся величиной, как это нетрудно видеть из свойства скобок Пуассона (50).

4. Свойства скобок Пуассона

Скобки Пуассона двух произвольных функций обобщенных координат и импульсов механической системы обладают следующими свойствами:

1 для любой функции f(p,q,t) и постоянной с

{f, c} = 0;                                                              (53)

2 для любых функций f(p,q,t) и g(p,q,t) скобки Пуассона антисимметричны:

{f, g} = –{g, f};                                                         (54)

3 скобки Пуассона обладают очевидным свойством линейности по обоим аргументам, а именно: для любых функций f(p,q,t), g(p,q,t), h(p,q,t) и числа с

{f + g,h} = {f,h}+{g,h}, {cf,g}=c{f,g};                                    (55)

4 для любых функций f(p,q,t), g(p,q,t), h(p,q,t) выполняется следующее тождество (тождество Якоби)

{f,{g, h}}+{h,{f, g}}+{g,{h, f}} =0.                                       (56)

Доказательство свойств (53) – (55) непосредственно вытекает из определения скобки Пуассона (50). Доказательство тождества Якоби (56) можно получить, записывая скобки Пуассона в левой части (56) в индексной форме записи и принимая во внимание симметрию смешанных производных по переменным дифференцирования.

Из (49) и тождества Якоби (56) следует, что если функции f(p,q,t) и g(p,q,t) являются различными интегралами движения: df/dt = 0, dg/dt = 0, то их скобка Пуассона также будет интегралом движения:

.                                                         (57)

Таким образом можно отыскать все линейно независимые интегралы движения механической системы.

Рассмотрим еще несколько важных следствий, вытекающих непосредственно из определения скобок Пуассона. В частном случае, когда g = q^k, либо g = p_k

.                                            (58)

Отсюда видно, что скобка Пуассона обобщенных импульсов и координат равна нулю, а для одноименных импульсов и координат равна единице:

                                     (59)

Аналог последних соотношений (59) в квантовой механике приводит к соотношениям неопределенности Гайзенберга. Переменные q^k и p_k, удовлетворяющие условиям (59), называются канонически сопряженными величинами.