Министерство образования Республики Беларусь

Учреждение образования

«Международный государственный экологический университет

имени А. Д. Сахарова»

Факультет мониторинга окружающей среды

А. И. Тимощенко

лагранжева и гамильтонова формулировки классической механики.

теория гамильтона – Якоби

учебное пособие по дисциплине «Теоретическая механика»

для студентов специальности 1-100 01 01

«Ядерная и радиационная безопасность»

Минск 2012

Рекомендовано к печати Научно-методическим советом МГЭУ им. А.Д. Сахарова

Рецензенты:

Содержание

1. Основы механики Лагранжа 4

1.1. Функция Лагранжа, конфигурационное пространство и действие механической системы 4

1.2. Вариационный принцип Лагранжа. Уравнения Лагранжа 5

1.3. Примеры функций Лагранжа для различных механических систем 7

1.4. Понятие о связях 10

1.5. Основные свойства функции Лагранжа 13

1.6. Учет неконсервативных сил в механике Лагранжа 14

2. Некоторые интегралы движения 16

3. Понятие о механике Гамильтона 17

3.1. Функция Гамильтона и уравнения Гамильтона. Фазовое пространство 17

3.2. Вариационный принцип Гамильтона 18

3.3. Дифференцирование величин по времени. Законы сохранения 18

3.4. Свойства скобок Пуассона 19

3.5. Канонические преобразования 20

3.6. Канонически сопряженные обобщенные координаты и импульсы пробного заряда во внешнем электромагнитном поле 24

4. Понятие о теории Гамильтона - Якоби 27

Классическая механика в рамках задач, в которых не рассматриваются необратимые потери энергии (например, трение), может быть построена несколькими эквивалентными способами – механика Ньютона, механика Лагранжа, механика Гамильтона, формулировка механики, основанная на уравнении Гамильтона – Якоби.

Традиционный, ньютоновский подход, основанный на формулировке трех законов Ньютона для материальной точки с последующим развитием аппарата теории на системы материальных точек, моделирующих реальные тела, широко применяется в науке и технике. Он позволяет сформулировать любую задачу об описании механического движения, в том числе, и при наличии необратимых процессов.

Другие формулировки механики имеют применение, строго говоря, лишь в случае отсутствия диссипативных сил. Такие механические системы часто называются гамильтоновыми. Несмотря на более узкую область применения, механика Лагранжа, механика Гамильтона и формулировка механики, основанная на уравнении Гамильтона – Якоби обладают рядом преимуществ при решении некоторых классических задач, например, таких, как движение заряженной пробной частицы во внешних электрическом и магнитном полях, результаты которых широко применяются в теории взаимодействия ионизирующего излучения с веществом. Основные представления механики Лагранжа и механики Гамильтона, развитый в их рамках математический аппарат имеют определяющее значение при переходе от классической механики к квантовой механике, при формулировке теории классических полей, лежащей в основе теории элементарных частиц и физики высоких энергий.

Более подробное изложение данного материала можно найти в соответствующих руководствах по теоретической механике для вузов. Существует обширнейшая библиография по различным формулировкам классической механики, для более глубокого ознакомления с которыми можно порекомендовать книги [1–4].

1. Основы механики Лагранжа

1. Функция Лагранжа, конфигурационное пространство и действие механической системы

Механика Лагранжа основана на понятиях функции Лагранжа и действия механической системы. В простейших случаях в нерелятивистской механике под функцией Лагранжа L механической системы понимается разность кинетической E и потенциальной U энергий этой системы:

L = E  U.                                                                 (1.1)

В некоторых случаях функцию U можно рассматривать в обобщенном смысле, даже включая в нее явную зависимость от времени (см. ниже).

Функция Лагранжа зависит от координат и скоростей материальных точек, входящих в систему. Поскольку для описания движения материальных точек часто бывает удобно использовать криволинейные координаты, или вводить координаты точек каким либо способом, приспособленным к специфике конкретного движения¹, то такие координаты называют обобщенными координатами, а их первые производные по времени - обобщенными скоростями. Обычно обобщенные координаты обозначаются буквой qⁱ с индексом i, указывающим ее номер. Обобщенные скорости обозначают точками над соответствующими обобщенными координатами: 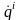. Число независимых координат s, опи­сывающих движение механической системы, называется числом степеней свободы; i = 1,...,s. Для краткости всю совокупность обобщенных координат обозначают одной буквой q, а всю совокупность обобщенных скоростей – буквой 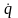. Обобщенные координаты могут рассматриваться как координаты точки в некотором воображаемом пространстве, называемом конфигурационным пространством. Его размерность равна числу степеней свободы. Положение механической системы в данный момент времени (совокупность значений обобщенных координат) изображается точкой в конфигурационном пространстве. Кривая в конфигурационном пространстве будет описывать движение механической системы. Ее называют траекторией механической системы в конфигурационном пространстве (не путать с траекторией материальной точки в пространстве).

Действием механической системы называется интеграл

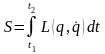,                                                             (1.2)

в котором моменты начала t₁ и конца t₂ наблюдения за механической системой фиксированы, а функция Лагранжа содержит q и 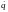как совокупности независимых переменных. Из (1.2) видно, что действие  это число, значение которого при фиксированных моментах t₁ и t₂ определяется только формой зависимости обобщенных координат от времени. Иными словами, в правой части (1.2) определено отображение, ставящее в соответствие некоторой совокупности функций времени q определенное при данных t₁ и t₂ число S. Такое отображение, как известно из курса линейной алгебры, называется функционалом.

2. Вариационный принцип Лагранжа. Уравнения Лагранжа

В основе механики Лагранжа лежит утверждение, что условия, при которых действие имеет экстремум (минимум), являются уравнениями движения. Решения этих уравнений задают траектории движения. Эти траектории называются «истинными».

Для решения задачи о нахождении экстремума функционала (1.2) нельзя применять методы исследования на экстремум, развитые для функций, так как форма зависимости обобщенных координат от времени не является числом. Однако отличие друг от друга различных видов зависимостей qⁱ и 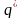можно вполне однозначно охарактеризовать функцией, называемой вариацией функции qⁱ: . Рассматривая заданные на отрезке [t₁,t₂] всевозможные зависимости от времени обобщенных координат, можно ввести понятие бесконечно малой вариации qⁱ. По отношению к этим бесконечно малым величинам можно развить, так называемое, вариационное исчисление, аналогичное исчислению бесконечно малых, которое изучается в традиционном курсе математического анализа и которое будет обосновано в дисциплине «Методы математической физики». В частности, правила вычисления бесконечно малых вариаций сложных функций и функционалов многих переменных формально аналогичны записи полного дифференциала функции многих переменных. Так, для функции Лагранжа имеем (по повторяющимся индексам производится суммирование от 1 до s)

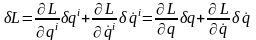,                                          (1.3)

где правая часть второго равенства является прямой записью левой части¹. Детальное обоснование методов вариационного исчисления можно найти в соответствующих руководствах (см., например, [1]). Ниже будет дан упрощенный подход, в котором отмечаются лишь важнейшие идеи вариационного исчисления без их строгого обоснования.

Чтобы найти экстремум функционала действия, нужно рассчитать его бесконечно малую вариацию. Условия, при которых она обратится в нуль, и будут искомыми услови­ями экстремума. Вид этих условий существенно зависит от поведения вариаций на концах отрезка [t₁,t₂]. Это поведение должно быть задано дополнительными условиями, определяющими тип вариационной задачи на экстремум. В нашем случае, поскольку моменты t₁ и t₂ фиксированы, при варьировании действия имеет смысл говорить о траекториях, по которым система может переходить в конфигурационном пространстве из положения, отвечающего моменту времени t₁, в положение, отвечающее моменту времени t₂. Это значит, что на концах отрезка [t₁,t₂]

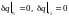_­ .                                                         (1.4)

В основе метода, позволяющего вывести искомые условия экстремума, лежит идея о том, что вариации формы функций q не зависят от времени (форму функции можно менять одновременно во всех точках конфигурационного пространства за исключением начала и конца движения). Это позволяет переставлять между собой операции дифференцирования по времени и варьирования по форме функций q, а также записать, что

.          

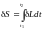Подставим сюда (1.3), в котором, пользуясь возможностью переставить местами порядок следования варьирования и дифференцирования по времени:

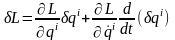,                                                    (1.3)

выделим полную производную по времени. Получим

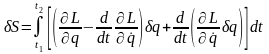,                                            (1.5)

Интеграл от полной производной по времени в (1.5) может быть без труда вычислен, и результат этого вычисления 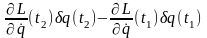при условиях (1.4) обращается в нуль. Вариация действия при выполнении условий (1.4) примет вид

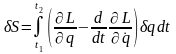.                                                      (1.6)

Поэтому равенство нулю вариации действия

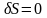,                                                                    (1.7)

являющееся необходимым условием существования минимума функционала (1.2), возможно лишь при обращении в нуль подынтегрального выражения, стоящего в круглых скобках в (1.6). Поскольку все вариации qⁱ линейно независимы, то

.                                                           (1.8)

Уравнения (1.8) называются уравнениями Лагранжа для системы материальных точек (символ вида L/q может быть представлен как ковектор с координатами L/qⁱ). В этих уравнениях

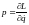                                                                   (1.9)

играет роль ковектора обобщенных импульсов, а L/q  ковектора обобщенных сил.

При взаимно-однозначных, по крайней мере, дважды непрерывно дифференцируемых преобразованиях обобщенных координат

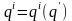, ,                                                   (1.10)

где k' принимает значения от 1' до s' = s, а q означает совокупность новых координат , 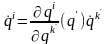оказывается функцией не только новых обобщенных скоростей, но и новых обобщенных координат. Поэтому

                                  (1.8)

Взаимно-однозначные дважды непрерывно дифференцируемые преобразования вида (1.7) называются точечными преобразованиями в конфигурационном пространстве. Выбор геометрической модели конфигурационного пространства зависит от способа описания механической системы. Пока не возникает особой нужды в использовании неевклидовой геометрии, можно считать конфигурационное пространство евклидовым. Тогда коэффициенты линейной связности необходимо вводить лишь в случае использования криволинейных координат в качестве обобщенных координат.

правило преобразования коэффициентов линейной связности

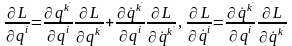                                  (1.8)

позволяет обеспечить общую ковариантность выражений в (1.5) и, следовательно, независимость вариации действия от выбора обобщенных координат.