3. Примеры функций Лагранжа для различных механических систем

Рассмотрим функцию Лагранжа и понятие обобщенных координат для некоторых механических систем.

1. Материальная точка. Для нерелятивистской точечной частицы массы m, движущейся в пространстве под действием силы 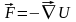, функция Лагранжа согласно (1.1) может быть представлена в виде

,                                                         (1.13)

где  радиус-вектор положения частицы, а  ее скорость. Если в качестве обобщенных координат частицы взяты декартовы координаты точки , являющиеся в то же время координатами радиус-вектора , то легко усмотреть в ковекторе L/q ковариантный вектор . Тогда ковектор обобщенных импульсов (1.12) представляет собой следующий ковариантный вектор . Подстановка этих производных в уравнения Лагранжа (1.11) приводят к обычным уравнениям Ньютона для частицы, движущейся в поле потенциальных сил:

.                                                       (1.14)

Если описание движения частицы удобно производить в цилиндрической системе координат q¹ = , q² = , q³ = z, связанных с декартовыми координатами соотношениями: x = cos, y = sin, z = z, то в этих координатах , и функция Лагранжа (1.13) принимает вид

.                                      (1.13)

Соответствующие обобщенные импульсы, согласно (1.12), в этом случае будут определяться выражениями

                             (1.15)

Обобщенные импульсы и представляют собой проекции вектора импульса на базисные векторы и натурального базиса цилиндрической системы координат. В то же время обобщенный импульс p₂ = p_ оказывается проекцией вектора момента импульса частицы 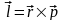на базисный вектор . Поэтому такие величины называются обобщенными импульсами. В рассматриваемом случае они являются проекциями соответствующих векторов импульса и момента импульса на векторы натурального ковариантного базиса цилиндрической системы координат (проверьте!).

Переход от декартовых координат к цилиндрическим может рассматриваться как частный случай точечных преобразований (1.7). Коэффициенты линейной связности в натуральном базисе цилиндрической системы координат

                                                        (1.16)

позволяют записать уравнения Лагранжа (1.11) с учетом (1.6) в следующем виде:

Уравнения Лагранжа (1.11) для материальной точки с координатами в цилиндрической системе координат q¹ = , q² = , q³ = z

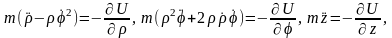                           (11)

эквивалентны (11), записанному относительно натурального базиса цилиндрической системы координат (проверьте!).

2. Система материальных точек. Система частиц, взаимодействующая между собой посредством потенциальных сил, зависящих только от положения этих частиц, будут описываться функцией Лагранжа следующего вида:

,                                                 (12)

где 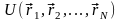 сумма потенциальной энергии взаимодействия системы частиц и потенциальных энергий каждой из них во внешнем поле:

.                                   (13)

В качестве обобщенных координат системы здесь естественным образом выступают 3N координат материальных точек, например, совокупность 3 декартовых координат N материальных точек.

Система уравнений Лагранжа может быть получена из (12) непосредственно в виде второго закона Ньютона вида (11), сформулированного для каждой частицы в отдельности:

,                                                       (14)

где операторы

                                                         (15)

определяются как операторы дифференцирования по координатам каждой из частиц в отдельности.

Вместо радиус-векторов , описывающих положение отдельных частиц, можно ввести любые другие координаты, которые могут оказаться удобными для описания системы. При этом одночастичная интерпретация таких координат теряется, зато появляются возможности использовать переменные, которые позволяют описать коллективное движение системы в целом. Например, представим в виде

,                                                            (16)

где

                                       (17)

радиус-вектор центра инерции системы в нерелятивистском случае, а определяет положение точек системы относительно центра инерции. Из (16) и (17) вытекает, что

.                                                (18)

Подстановка (16) в

в теории движения электронов и ядер в молекулах, которые во многих задачах можно рассматривать как заряженные материальные точки, взаимодействующие между собой по закону Кулона, широко используются т.н. координаты Якоби, которые для системы из N частиц вводятся следующим образом:

                                              (16)

Последнее выражение представляет собой радиус-вектор центра инерции (центра масс) системы материальных точек в нерелятивистском приближении. Новые координаты (16) имеют простой смысл: – это вектор перемещения из точки 2 в точку 1, – вектор перемещения из точки 3 в точку, являющуюся центром масс системы, состоящей из двух материальных точек 1 и 2, – вектор перемещения из точки 3 в точку, являющуюся центром масс точек 1,2,3 и т.д. Обратное к (16) преобразование можно вывести непосредственно методами линейной алгебры, применение которых в общем случае оказывается достаточно громоздким (см. Приложение). Приведем здесь окончательный ответ:

,                                                            (17)

где

,                                             (18)

является радиус-вектором, который определяет положение материальной точки относительно центра инерции системы, а

                                               (19)

При этом сумма в (18) обращается в ноль при  = N.

После подстановки (17) в (12), получим

,                                                 (19)