Понятие о связях
Материальные точки в системе могут находиться в определенной связи друг с другом так, что движение каких-то из материальных точек будет зависеть от движения других материальных точек. В этом случае говорят, что в системе имеются связи. В механике связью называют материальные объекты, которые ограничивают свободу перемещения рассматриваемой механической системы. Эти ограничения могут быть записаны
Простейшим примером связанной системы
материальных точек является система
двух материальных точек, расстояние
между которыми
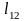в процессе движения не меняется:
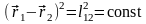. (13)
Число s независимых коорднат системы будет равно s = 3 (координаты каждой из частиц) 2(частицы) 1(условие вида (11)) = 5. Например, такой системой может оказаться двухатомная молекула, не совершающая колебаний, положение которой можно задать тремя декартовыми координатами ее центра инерции и двумя углами, задающими ориентацию оси молекулы.
Если система N
материальных точек движется в плоскости,
характеризуемой вектором нормали
,
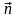то их радиус-векторы должны подчиняться
системе N уравнений
,
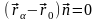(14)
где
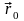радиус-вектор
некоторой наперед заданной точки
плоскости. В этом случае число независимых
координат, описывающих систему, будет
равно s = 3N r ,
где r – ранг матрицы
системы однородных уравнений (14).
Твердое тело в механике рассматривается как система материальных точек, взаимное расстояние между которыми не меняется в процессе движения. Если речь идет о свободном движении твердого тела, то его положение в любой момент времени можно охарактеризовать 3 координатами одной из наперед заданных точек в пространстве (не обязательно лежащей внутри этого тела!) и 3 углами, составляемыми с осями некоторой наперед заданной декартовой системы координат с 3 взаимно перпендикулярными осями, жестко связанными с этим телом. В этом случае определение положения твердого тела возможно путем задания 6 обобщенных координат. Если одна из точек твердого тела закреплена, то его положение в пространстве будет определяться 3 углами, которые жестко связанные с телом оси составляют с осями некоторой декартовой системы координат, т.е. 3 обобщенными координатами.
Условия вида (13) или (14) имеют одно общее свойство: они не зависят от времени. В общем случае r независимых условий вида
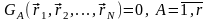, (15)
наложенных на координаты материальных точек системы, позволяют использовать для описания ее движения лишь s = 3N r координат. Эти координаты могут иметь смысл некоторых угловых, или каких-либо других величин, и поэтому называются обобщенными координатами.
В общем случае удерживающими связями в механике называются уравнения, содержащие время и скорости частиц:
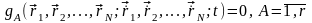.1 (17)
Если все уравнения (17) путем интегрирования приводятся к виду
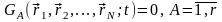, (18)
то описываемые ими связи называются голономными или геометрическими, а механическая система с такими связями тоже будет называться голономной. В случае, когда хотя бы некоторые из функции gА в уравнениях связей в левой части (18) явно зависят от времени t, то голономная система называется реономной. Связи, описываемыми уравнениями вида (15), называются стационарными, или склерономными, а сама механическая система – склерономной.
Примером неголономной2 системы является шар, катящийся без проскальзывания по неподвижной плоскости. В точке касания скорость точки шара равна нулю. Это условие не интегрируемо, так как в другие моменты времени, в т.ч. и во все сколь угодно мало отличающиеся от момента касания, скорость данной точки шара отлична от нуля. Неголономные связи часто встречаются в подвижных частях механизмов, соприкасающихся друг с другом без проскальзывания (контакт качения), например, в подшипниках.
Для реономной системы условия (18)
позволяют выделить s = 3N r
обобщенных координат qi,
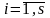и, вообще говоря, построить зависимости
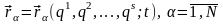. (19)
Подставляя (19) в первое слагаемое в (11), выражающее собой кинетическую энергию системы материальных точек, можно получить ее выражение в обобщенных координатах:
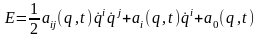, (20)
где
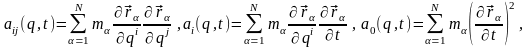(21)
а по повторяющимся в (20) попарно сверху и снизу индексам ведется суммирование от 1 до s.
В частности, кинетическая энергия склерономной системы нерелятивистских частиц представляет собой квадратичную форму, построенную на обобщенных скоростях:
. (22)
В этом случае коэффициенты квадратичной формы aij зависят только от обобщенных координат.
При подстановке (19) в выражение для потенциальной энергии, последняя может стать функцией не только обобщенных координат, но и времени:
.
(23)
Для склерономных систем существуют такие системы обобщенных координат, что потенциальная энергия от времени не зависит. Если в некоторой точке конфигурационного пространства с координатами q = q0
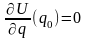(24)
(точка экстремума потенциальной энергии), то вблизи этой точки потенциальную энергию можно разложить в ряд Тейлора, несколько первых слагаемых которой с учетом (24) представятся в виде
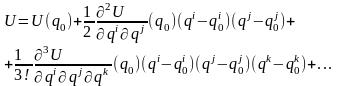(25)
Пользуясь
произволом в задании начала отсчета
потенциальной энергии (и функции
Лагранжа, см. ниже), и переходя к новым
обобщенным координатам
,
потенциальную энергию системы (25) можно
переопределить в этом приближении
следующим образом:
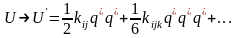, (26)
где
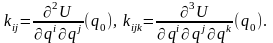(27)
Это представление потенциальной энергии применимо в широком классе случаев движения, которые рассматриваются в теории колебаний.
В случае неголономной системы все уравнения (17), или какая-то их часть оказываются неинтегрируемыми. В этом случае принцип стационарного действия не применим в сформулированном выше виде. Его необходимо рассматривать вместе с условиями (17) как условный экстремум, пользуясь методом неопределенных множителей Лагранжа. Рассмотрение этого вопроса выходит за рамки настоящего пособия.
Иногда связи определяются не уравнениями вида (17), а неравенствами, например,
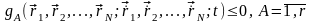. (28)
В этом случае связи называются неудерживающими, либо освобождающими, либо односторонними.
Все связи делят еще на идеальные и реальные. К идеальным связям относят любые связи без трения. К реальным связям относят связи с трением.