2. Некоторые интегралы движения

Обобщенная координата qⁱ называется циклической, если для нее выполняется условие

.                                                                    (37)

Из уравнений Лагранжа видно, что соответствующий обобщенной координате qⁱ обобщенный импульс p_i подчиняется закону сохранения:

.                                                           (38)

Это  частный случай интеграла движения.

Другой пример интеграла движения, возникающего при некоторых условиях, доставляет следующее рассуждение. Свернем обе части (35) с вектором . Справа получим выражение , имеющее смысл мощности результирующей обобщенных неконсервативных сил. А выражение, получаемое в левой части,

,

можно преобразовать к виду:

,

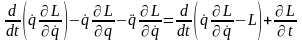что в результате дает

.                                                    (39)

В частном случае, когда функция Лагранжа не зависит явно от времени, а также, при условии, что работа неконсервативных сил равна нулю (что возможно, например, в случае стационарного магнитного поля), из (39) получим закон сохранения

                                                                 (40)

величины

.                                                     (41)

Эту величину называют полной механической энергией системы. Будучи выраженной только как функция обобщенных импульсов и координат, она называется функцией Гамильтона системы, которую, так же, как и функцию Лагранжа, можно постулировать, и рассматривать соответствующий вариационный принцип. Об этом речь пойдет в следующем пункте.

3. Понятие о механике Гамильтона

3. 1. Функция Гамильтона и уравнения Гамильтона. Фазовое пространство

Уравнения Лагранжа (1.8) являются дифференциальными уравнениями второго порядка. Можно понизить их порядок, рассматривая обобщенные импульсы (1.7) наряду с обобщенными координатами как независимые переменные. Однако функция Лагранжа, по своему определению, является функцией обобщенных координат и обобщенных скоростей, что выражается, в частности, записью ее полного дифференциала:

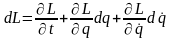.                                                 (42)

Чтобы выделить в этом выражении дифференциал функции, зависящей от переменных q p, перепишем, учитывая (1.8), второе слагаемое в (42) в следующем виде: . Перенося полный дифференциал в левую часть (42), и вводя обозначение (41), получим, что вновь введенная функция H является функцией обобщенных координат и обобщенных импульсов, так как ее полный дифференциал согласно (1.8), (41) и (42) имеет вид

.                                                   (43)

Если задана функция (41), как функция обобщенных координат и импульсов, то из (43) и определения полного дифференциала функции многих переменных получим

.                                                        (44)

Тем самым, мы получили систему 2s уравнений первого порядка, описывающие движение механической системы. Они называются уравнениями Гамильтона, а функция H – функцией Гамильтона. Если функция Лагранжа имеет вид (1.1), то можно показать, что функция Гамильтона есть просто сумма кинетической и потенциальной энергий системы частиц, то есть она определяет полную механическую энергию системы:

H = E + U.                                                               (45)

В гамильтоновой механике можно говорить не просто о положении системы в данный момент времени, а о состоянии системы, которое характеризуется наряду с обобщенными координатами еще и набором обобщенных импульсов. Воображаемое пространство, в котором точки нумеруются 2s независимыми координатами, в качестве каковых выступают s обобщенных координат и s обобщенных импульсов (их потом, правда, произвольными непрерывными преобразованиями координат в этом пространстве можно перемешать между собой) называется фазовым пространством. Совокупность состояний, которые механическая система проходит в течение некоторого времени, называется фазовой траекторией системы.