5. Основные свойства функции Лагранжа

Функция Лагранжа обладает следующими общими свойствами.

1 Если механическая система состоит из двух изолированных друг от друга подсистем А и В, то функция Лагранжа составной системы L может быть представлена в виде суммы функций Лагранжа отдельных подсистем

L = L_A + L_B.                                                                  (29)

Если же системы А и В взаимодействуют между собой посредством потенциальных сил, то в правой части (29) появится слагаемое  потенциальная энергия взаимодействия частей U_AB:

L = L_A + L_B + U_AB.                                                             (30)

Из уравнений Лагранжа (1.8) видно, что эти уравнения сами по себе позволяют определить функцию Лагранжа с точностью до произвольного множителя. Однако принцип аддитивности для изолированных подсистем (29) говорит о том, что у каждой изолированной подсистемы этот множитель должен быть одинаков и, следовательно, он зависит лишь от выбора системы единиц.

2 Если добавить к функции Лагранжа полную производную некоторой функции обобщенных координат и времени f(q,t), т.е. перейти от функции Лагранжа 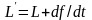, то соответствующий ему функционал действия согласно определению (1.2) превратится в . При варьировании действия с условиями (1.4) вариации дополнительных слагаемых в обратятся в ноль. Поэтому уравнения Лагранжа (1.8) будут выполняться и для функции Лагранжа с произвольной функцией f(q,t). В частности, функцию Лагранжа (и, соответственно, потенциальную энергию) можно задавать с точностью до добавления произвольной постоянной.

3 Функция Лагранжа свободной частицы не должна зависеть от ее координат, так как в противном случае частицу нельзя было бы считать свободной. Поэтому функция Лагранжа свободной частицы должна рассматриваться как функция исключительно ее скорости . Поскольку функция Лагранжа является скалярной величиной, то для свободной частицы она может зависеть только от квадрата вектора скорости:

.                                                              (31)

Из этой зависимости вытекает, что , тогда уравнения Лагранжа (1.8) приводят к выводу о сохранении величины

.                                                             (32)

Так как для свободной частицы функция Лагранжа зависит только от скалярного квадрата ее скорости (28), то , и из (32) вытекает, что

.                                                               (33)

Этот результат выражает принцип инерции и, соответственно, допустимость существования инерциальных систем отсчета.

В нерелятивистской механике радиус-вектор материальной точки в инерциальной системе отсчета K', движущейся со скоростью относительно инерциальной системы отсчета K, начало отсчета которой проходит через начало отсчета K в момент времени t = t' = 0, связан радиус-вектором материальной точки в этой системе отсчета преобразованием Галилея

,                                                          (34)

которое не меняет формы уравнений Лагранжа (1.8) (проверьте!) и является частным случаем точечных преобразований (1.8), удовлетворяющим условию (9).