11. Основные понятия теории графов.

Основные понятия:

Пусть V— непустое множество,X— набор пар элементов изV. В набореX могут встречаться пары, состоящие из одинаковых элементов, а также одинаковые пары. МножествоVи наборXопределяютграф с кратными ребрамиG=(V,X). Элементы множестваVназываютсявершинамиграфа, а элементы набораX—ребрамиграфа.

Если x=(u,v) — ребро графа, то вершиныuиvназываютсяконцами ребраx. Если вершинаvявляется концом ребраx, то говорят, чтоvиx—инцидентны.

Вершины uиvграфа называютсясмежными, если существует ребро графа, соединяющее их. Два ребра называются смежными, если они имеют общую вершину. Степенью вершиныv(обозначенияdeg(v)) называется число ребер графа, инцидентных вершинеv.

Последовательность

, (*)

в которой чередуются вершины и ребра и при этом для каждого i=1,…,n-1 реброимеет вид, называется маршрутом, соединяющим вершиныи. Число ребер в маршруте называется его длиной.

Маршрут, в котором все ребра разные, называется цепью. Маршрут, в котором все вершины разные, называетсяпростой цепью. Маршрут (*) называетсязамкнутым, если=. Замкнутый маршрут, в котором все ребра различные, называетсяциклом. Цикл, в котором все вершины, кроме первой и последней, разные, называетсяпростым циклом.

Граф называется связным, если для любых двух различных его вершин существует цепь (маршрут, простая цепь), соединяющая их.Расстояниеммежду вершинами связного графа называется длина кратчайшей цепи, соединяющей эти вершины.

Подграфом графаG называется граф, все вершины и ребра которого содержатся среди вершин и ребер графаG. Подграф называется собственным, если он отличен от самого графа.Компонентой связности графаGназывается его связный подграф, не являющийся собственным подграфом никакого другого связного подграфа графаG.Остовнымназывается граф, содержащий все вершины графа. ГрафыG=(V,X) иH=(U,Y) изоморфны, если существуют такие два взаимно однозначных соответствия, что для всякого ребрасправедливо соотношение.

Двудольным называется граф, множество вершин которого можно разбить на два непустых подмножества (доли)V₁иV₂таким образом, что никакие две вершины из одной и той же доли не являются смежными.

Деревом называется связный граф без циклов.

Теорема Кёнига: Граф является двудольным тогда и только тогда, когда в нем отсутствуют циклы нечетной длины.

Задачи.

11.1. Показать, что для произвольного графаG=(V,X) справедливо равенство

.

11.2. Изобразить все попарно неизоморфные 4-вершинные графы без петель и кратных ребер.

11.3. Показать, что в любом графе без петель и кратных ребер, содержащем не менее 2 вершин, найдутся 2 вершины с одинаковыми степенями.

11.4. Среди пар графов, изображенных на рис.1-3, указать пары изоморфных и неизоморфных графов.

12. Элементы теории кодирования

Основные понятия:

Пусть — алфавит. Конечная последовательность символов изUназываетсясловомв алфавитеU. ЧерезS(U) обозначим множество всех слов в алфавитеU.

Пусть UиB— два алфавита. Однозначное отображениеFпроизвольного подмножествана подмножестваназываетсякодированием. При этом слова изMназываютсясообщениями, а их образы —кодами сообщений. МножествоСназываетсякодом множества сообщенийМ. АлфавитU называетсяалфавитом сообщений, а алфавитВ —кодирующим алфавитом. КодированиеF называетсявзаимно однозначным, если каждый код сообщения является кодом ровно одного сообщения.

Пусть задано отображение букв алфавитаUв множествоS(B) вида

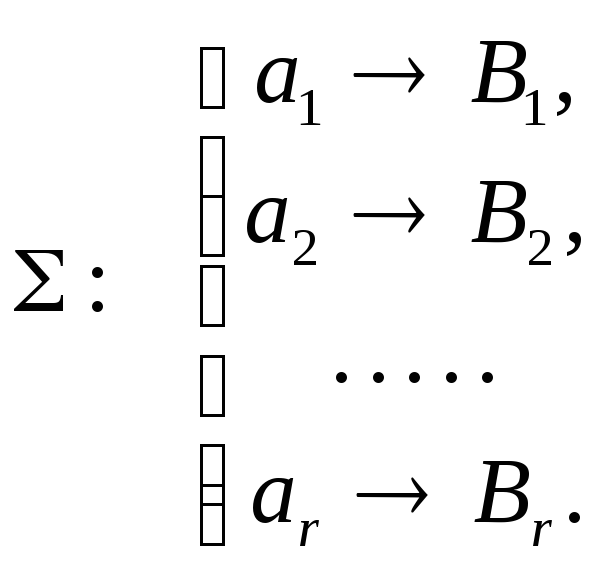
Кодирование , удовлетворяющее свойствам:

1. 

2. 

где под произведением слов АВ понимается приписывание словаВ справа к словуА, называетсяалфавитным кодированием,задаваемым схемой .

Если тоназывается префиксом, а— суффиксом словаВ. Префикс (суффикс) словаВ называетсясобственным, если он отличен от пустого слова (обозначаемого через) и от самого словаВ. Длиной слова называется число букв в нем. Схемаобладает свойством префикса, если для любых слови() из С() словоне является префиксом слова.

Теорема. Алфавитный код С() является однозначно декодируемым тогда и только тогда, когда в графеотсутствуют контуры и петли, проходящие через вершину.