5. Замкнутые классы и полнота Основные понятия

Пусть K — некоторое множество функций алгебры логики. Замыканием [K] множества K называется совокупность всех функций из Р₂, являющихся суперпозициями функций из множества K. Множество K называется замкнутым классом, если [K]=K. Пусть K – замкнутый класс в Р₂ . Подмножество P из K называется функционально полной системой в K, если [P] =K.

Множество K’, содержащееся в замкнутом классе K (в т.ч. K=P₂), называется предполным классом в K, если оно не является полной системой в K, но для всякой функции выполняется равенство

Самодвойственные функции

Функция называется двойственной к , если = . Двойственная функция обозначается .

Функция называется самодвойственной, если = . Класс самодвойственных функций обозначается S.

Линейные функции

Функция называется линейной, если она представима в виде

Множество всех линейных функций обозначается L .

Функции, сохраняющие константу

Говорят, что функция сохраняет константу 0 (константу 1), если f(0,0,...,0)=0 (cоответственно, f(1,1,...,1)=1). Множества функций, сохраняющих константу 0 или 1, обозначаются соответственно T₀ и T₁ .

Монотонные функции

Булева функция называется монотонной, если для любых двух наборов из , таких, что имеет место неравенство

. В противном случае функция называется немонотонной.

Вершина куба называется нижней единицей (верхним нулем) монотонной функции , если =1 ( =0 ) и для всякой вершины из вытекает, что =0 (соответственно из вытекает =1). Множество монотонных функций обозначается M.

Каждое из множеств T₀, T₁, S, L, M является замкнутым и предполным классом в P₂ .

Теорема. Система K полна в Р₂ тогда и только тогда, когда она целиком не содержится ни в одном из классов T₀, T₁, S, L, M.

ЗАДАЧИ

5.1. Является ли множество K замкнутым классом:

1) K ={0,1}; 2) K = { }; 3) K = { 1, };

4) K = {0, }.

5.2. Сведением к заведомо полным системам в P₂ , доказать полноту системы K:

1) K = { }; 2) K = { };

3) K = { }; 4) K = { }.

5.3. Доказать, что всякий предполный класс в Р₂ является замкнутым классом.

5.4. Является ли функция g двойственной к f, если

1) f = x y, g = x ~ y; 2) f = x y, g = y x .

5.5. Является ли функция самодвойственной:

5.6. Подсчитать число самодвойственных функций, существенно зависящих от переменных

5.7. Доказать, что если — самодвойственная функция, то .

5.8. Разлагая функцию f в полином Жегалкина, выяснить, является ли она линейной:

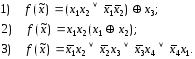
5.9. Доказать, что для любой ф.а.л. существует единственное разложение в полином Жегалкина.

5.10. Доказать, что если f — линейная функция и f const, то

5.11. Найти число линейных самодвойственных функций.

5.12. Доказать, что .

5.13. Доказать, что если на любых двух соседних наборах принимает противоположные значения,

то она линейная.

5.14. Показать, что всякая монотонная функция содержится не менее, чем в двух классах из { }.

5.15. Функция f не принадлежит множеству { } и принимает в точности одно значение, равное нулю.

Доказать, что она либо является шефферовской, либо существенно зависит лишь от одной переменной.

5.16. Какие из перечисленных ниже функций являются монотонными:

5.17. Подсчитать число функций в каждом из следующих множеств:

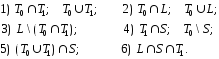
5.18. Показать, что если немонотонна, то существуют такие два вектора и из , различающиеся

ровно в одной координате, что , но .

5.19. Показать, что в Р₂ не существует предполных классов, отличных от классов T₀, T₁, S, L, M .

5.20. Используя критерий полноты, выяснить, полна ли система Р:

1) P = { }; 2) P = { };

3) P = {0, 1, }.

5.21. Доказать, что любую функцию из Р₂ можно представить через логические связки: конъюнкцию,

дизъюнкцию и отрицание.

5.22. Пусть и удовлетворяет условию = . Доказать, что если , то .

5.23. Из самодвойственной функции f с помощью подстановки на места переменных получить константу

5.24. Можно ли из функции f=(10110010) с помощью операции суперпозиции получить функцию g=(1000)?

5.25. Показать, что , где – совокупность всех функций, двойственных к линейным функциям.