21. Количество информации. Формула Хартли.

Пусть имеется множество N=2^k элементов. Пусть во множестве N помечен некоторый элемент. Каким кол-вом инф-ции (в битах) надо обладать для идентификации помеченного эл-та?

K=log₂ N, где N – кол-во элементов.

В формуле Хартли предполагается, что все элементы множества равновероятны.

Закон аддитивности:

Пусть имеется мн-во M1, содержащее N1 эл-тов и Хi принадлежит N1. M2 содержит N2 эл-тов и Хj принадлежит N2. Составим пары (Хi , Хj)

M=N1*N2

log₂(N1*N2)= log₂ N1 + log₂ N2

22. Формула Шеннона.

Пусть имеется случайная величина Х: Х1, Х2, Х3, … , Х_n с вероятностями р1, р2, р3, … , р_n

I(Xi) – кол-во информации при одном опыте

I(Xi) = log₂ 1/Pi

В каждом комплексе мы получаем различное кол-во информации.

Формула Шеннона:

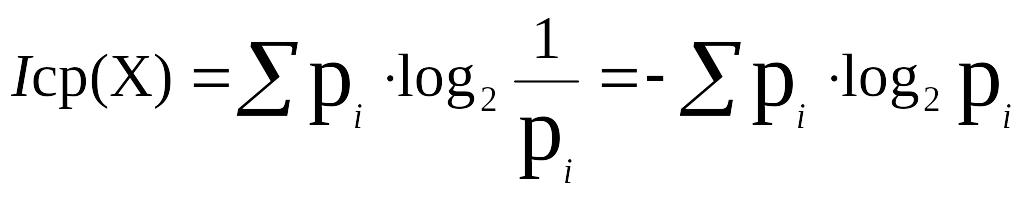
23. Энтропия источника сообщений. Свойства энтропии источника дискретных сообщений

Энтропия - это математическое ожидание по частным количествам информации сообщений, генерируемых источником. Безусловная энтропия источника вычисляется по формуле:

[бит/сообщ.]

Свойства энтропии:

1. Это величина вещественная, действительная, неотрицательная: 0<= <=1.

2. Энтропия достоверного события = 0.

, [бит/сообщ.]

Энтропия – это интегральная оценка

Не следует путать среднее значение информации с информацией, полученной в данном конкретном опыте.

-энтропия достоверного события.

;

;

;

;

Где .

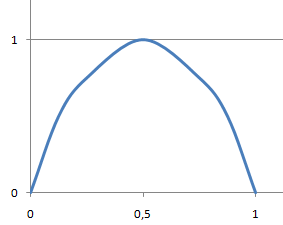
3. Энтропия альтернотивного сообщения максимальна при равной вероятности.

4. Энтропия максимальна, когда вероятности событий одинаковы.

;

- при условии равновероятности.

Реальные источники как правило имеют произвольный закон распределения и энтропия, вызванная неравенством распределения будет меньше max, а энтропия, вызванная неравенством распределения называется безусловной. Т.о. безусловная энтропия вызывается только неравенством распределения:

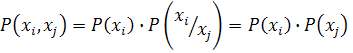- независимые события

Условная энтропия – термин применимый к зависимым событиям.

;

.

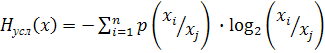24. Избыточность при передаче сообщений. Роль избыточности при передаче информации

Наличие в сообщении большего числа букв или в кодовой комбинации большего числа элементов, чем это минимально необходимо для передачи содержащегося в них количества информации, называют избыточностью. Расчет избыточности проводится по формуле:

Роль избыточности при передаче информации: избыточность позволяет обнаруживать и исправлять ошибки, и эта способность зависит от количества избыточных разрядов.

25. Математические модели сигналов. Спектральное представление сигналов.

Физ. природа сигнала зависит от канала связи. Для того, чтобы сигнал стал объектом научного исследования без относительно физ. природе, необх. указать путь создания его мат. модели. Различные мат. модели должны отражать различные с-ва сигналов. Сигнал можно изучать как аналитическое описание ф-ции, аргументом кот. явл. время. Можно изучать энерг. с-ва сигнала. Можно построить частотную модель сигнала (спектр). Ряд Фурье произвольной периодической ф-ции любого аргумента:

В математике ф-ция любого аргумента, а в ТПС – ф-ции, аргументом кот. явл. ВРЕМЯ – наз. ПРОЦЕСС.

Спектральные характеристики случайных процессов.

Гармонич. анализ детерминир. процесса явл. мощным средством исслед. и описания их. Естественно этот аппарат перенести на случ. процессы. Но случ. процесс имеет 2 особенности: 1)процесс не является абсолютно интегрируемым: 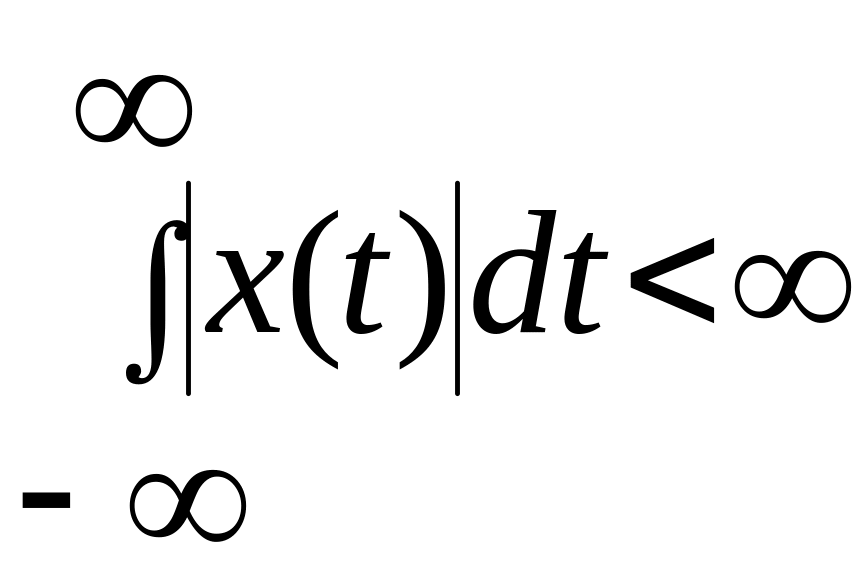. 2) Преобраз. Фурье случ. процесса есть тоже процесс случайный. Для обобщ. хар-тик случ. процесса необх. неслуч. величина. Спектральные хар-тики случ. процессов МОГУТ быть вычислены. Сущ. 2 пути их нахождения: I) Путь усреднения. Исходя из с-ва эргодичности случ. процесса.

I I) Путь, связ. с Фурье-преобраз. корреляционной ф-ции. Имеем кор. ф-цию , кот. зависит только от τ, то корреляц. ф-ция, связ. с энергетическим спектром Фурье-преобразования.

Ф-лы Винера-Хинчера: